Методы интегрирования.

Понятие первообразной функции. Неопределенный интеграл.

Интеграл - одно из центральных понятий математического анализа и всей математики. Оно возникло в связи с двумя основными задачами: 1) о восстановлении функции по заданной ее производной; 2) при вычислении площади, ограниченной графиком функции y=f(x), хє[a;b], прямыми x=a, x=b и осью Ox.

Указанные две задачи приводят к двум, связанным между собой, видов интегралов: неопределенного и определенного.

Элементы интегрального исчисления заложены в трудах математиков Древней Греции. Основные понятия теории интегрального исчисления разработаны в конце 17 столетия Ньютоном и Лейбницем. Далее историческое развитие интегрального исчисления связано с именами Эйлера, Коши, Римана и др.

Функция F(x) называется первообразной функции f(x) на интервале (a;b), если она дифференцируема на этом интервале .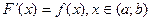

Но задача нахождения первообразной, решается неоднозначно.

Теорема.

Если F(x) первообразная функции f(x) на интервале (a;b),то всякая другая первообразная функции на этом самом интервале имеет вид F(x)+С.

Из этой теоремы следует, что множество функций F(x)+С, где С – произвольная постоянная определяет всю совокупность первообразных заданной функции.

Выражение F(x)+С называется неопределенным интегралом функции f(x) на интервале (a;b) и обозначается символом .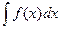

Операцию нахождения неопределенного интеграла от функции называют интегрированием этой функции.

З точки зрения геометрии, неопределенный интеграл является множеством кривых, каждая из которых называется интегральной кривой и образуется смещением одной из них параллельно самой себе вдоль оси Оу.

2. Свойства неопределенного интеграла.

1) Производная от неопределенного интеграла равна подынтегральной функции:

.

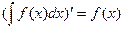2) Неопределенный интеграл от дифференциала данной функции равен сумме этой функции и произвольной постоянной:

.

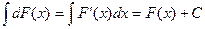3) Дифференциал от неопределенного интеграла равен подынтегральному выражению:

.

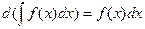4) Постоянный множитель можно выносить за знак интеграла:

.

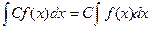5) Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:

.

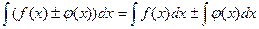6) Если

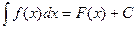
и 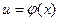произвольная функция, что имеет непрерывную производную, то

.

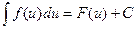Методы интегрирования.

І. Метод непосредственного интегрирования .

Данный метод интегрирования функций осуществляется по формулам интегрирования , которые приведены в таблице.

Таблица интегралов.

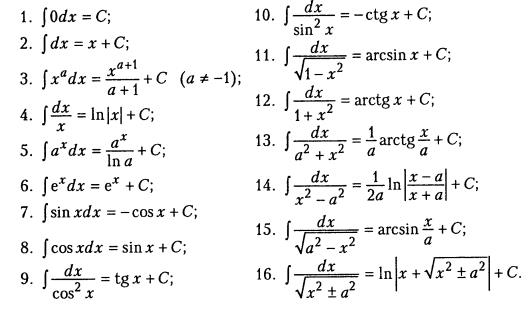
Пример.

Вычислить интеграл: а) 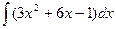; б)

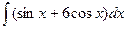
Решение:

а) .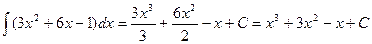

б) .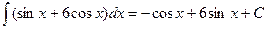

ІІ. Метод замены переменной (подстановки).

Суть этого метода заключается во введении новой переменной интегрирования. Подстановка подбирается так, чтобы полученные после преобразования новые интегралы были табличными, или сводились к ним.. Универсального метода подбора не существует, поэтому умение правильно определять подстановку приходит с практикой.

Пример.

Найти интеграл: а) ;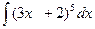

Решение: введем замену 3х+2=и, тогда du=3dx, и dx=1/3 du , сделаем подстановку полученных значений в данный интеграл

.

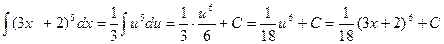ІІІ. Метод интегрирования по частям.

Суть такого метода заключается в использовании формулы интегрирования по частям:

.

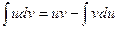Как правило, подынтегральное выражение, которое составляет произведение udv можно разбить на множители u и dv несколькими способами. Умение представить подынтегральную функцию через множители u и dv так, чтобы интеграл был более простым, вырабатывается в процессе практики.

Во время нахождения функции v по дифференциалу dv считают, что постоянная С=0, поскольку на конечный результат эта постоянная не влияет.

Пример.

Найти интеграл: а) ;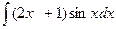

Решение: возьмем за и=2х+1, dv=sinxdx, найдя du=2dx, 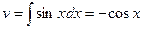, получим :

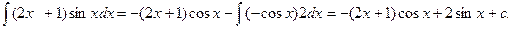
Контрольные вопросы.

1. Что называется первообразной данной функции? Привести примеры.

2. Сформулируйте теорему об общем виде первообразной.

3. Что называется неопределенным интегралом от данной функции?

4. Какие методы интегрирования вы знаете?

5. В чем состоит метод непосредственного интегрирования?

6. В чем заключается метод замены переменной?

7. Для каких функций метод замены переменной не может быть использован?

8. В чем состоит метод интегрирования по частям?

Литература:

В.П.Дубовик, И.И.Юрик «Высшая математика», К., 2003, ст.330-341