Электрический диполь
Электрическим диполем (диполем) называют систему, состоящую из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга (плечо диполя).
Основной характеристикой диполя (рис. 12.5) является его электрический момент (дипольный момент) — вектор, равный произведению заряда на плечо диполя I, направленный от отрицательного заряда к положительному:

Единицей электрического момента диполя является кулон-метр.
 Поместим диполь в однородное электрическое поле напряженностью Е (рис. 12.6).
Поместим диполь в однородное электрическое поле напряженностью Е (рис. 12.6).
На каждый из зарядов диполя действуют силы F+ = qE и F_ = = -qE, эти силы равны по модулю, противоположно направлены и создают момент пары сил. Как видно из рисунка, он равен
 |
По векторной форме
 |
 |
Таким образом, на диполь в однородном электрическом поле действует момент силы, зависящий от электрического момента и ориентации диполя, а также напряженности поля.
Рассмотрим теперь диполь в неоднородном электрическом поле. Предположим, что диполь расположен вдоль силовой линии (рис. 12.7). На него действуют силы
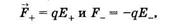
s где Е+иЕ_ — напряженности поля соответственно в месте нахождения положительного и отрицательного зарядов (на рис. 12.7 Е_ > Е+).
Значение равнодействующей этих сил
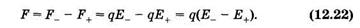
Введем отношение (Е_ — Е+)/1, характеризующее среднее изменение напряженности, приходящееся на единицу длины плеча диполя.Так как обычно плечо невелико, то приближенно можно считать
 |
где dE/dх — производная от напряженности электрического поля понаправлению оси ОХ, являющаяся мерой неоднородности электрического поля вдоль соответствующего направления. Из (12.23)следует, что
 |
тогда формулу (12.22) можно представить в виде
 |
Итак, на диполь действует сила, зависящая от его электрического Момента и степени неоднородности поля dE/dx. Если диполь ориентирован в неоднородном электрическом поле не вдоль силовой линии, то на него дополнительно действует еще и момент силы. Таким образом, свободный диполь ориентируется вдоль силовых линий и втягивается в область больших значений напряженности поля.
1. 1. 1.
 |
Многие медицинские приборы выдают информацию на регистрирующем устройстве (например, электрокардиограф), поэтому следует учитывать погрешности, характерные для этой формы записи (см. § 17.5).
 |
До сих пор рассматривался диполь, помещенный в электрическое поле, однако сам диполь также является источником поля. На основании (12.18) запишем выражение для электрического потенциала поля, созданного диполем, в некоторой точке А, удаленной от зарядов соответственно на расстояния r и r1 (рис. 12.8):
 |
где а — угол между вектором р и направлением от диполя на точку А (рис. 12.8). Используя (12.26), из (12.25) получаем
 |
Рассмотрим некоторые приложения формулы (12.27).
Пусть диполь, электрический момент которого равен р, находится в точке О (рис. 12.9), а его плечо мало. Используя (12.27), запишем разность потенциалов двух точек поля А и В, равноотстоящих от диполя (углы аА и ав показаны на рис. 12.9):
 |
Угол между р и прямой АВ или ОС обозначим α, /AOB = β углы аА = а + β/2 + α/2, ав = а - β/2 + α/2.
Учитывая эти равенства, выполним тригонометрические преобразования:
 |
Подставляя (12.29) в (12.28), имеем
 |
 |
Как видно из (12.30), разность потенциалов двух точек поля диполя, равноотстоящих от него (при данных е и г), зависит от синуса половинного угла, под которым видны эти точки от диполя (рис. 12.10), и проекции электрического момента диполя р cos α на прямую, соединяющую эти точки (рис. 12.11). Эти замечания справедливы в рамках тех ограничений, которые были сделаны при выводе формулы (12.27).
Пусть диполь, создающий электрическое поле, находится в центре равностороннего треугольника ABC (рис. 12.12). Тогда на основании (12.30) можно получить, что напряжения на сторонах этого треугольника относятся как проекции вектора р на его стороны:
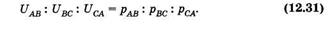
Дата добавления: 2020-11-18; просмотров: 566;











