Газопроницаемость полимеров. Диффузия

Диффузия - процесс выравнивания концентрации (n) частиц (атомов, молекул, ионов, электронов) в среде. При наличии градиента концентрации 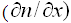частиц в веществе возникает поток этих частиц (J), выравнивающий их концентрации. Связь между потоком и коэффициентом диффузии (D) выражается первым законом Фика:

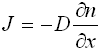
(5.4)

Это соотношение справедливо, когда размер системы в направлении градиента концентрации много больше длины свободного пробега частиц в среде, а изменение концентрации на расстоянии длины свободного пробега много меньше характерного значения концентрации частиц. Кроме того, предполагается отсутствие внешних полей, градиентов температуры и давления.

Коэффициент диффузии является функцией концентрации молекул пенетранта (диффузанта) (второй закон Фика) и в декартовых координатах выражается как:

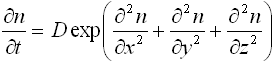
(5.5)

Про полимерные системы, диффузные характеристики которых можно описать первым и вторым законами Фика, говорят, что такие системы отвечают «фиковской диффузии».

Коэффициент диффузии зависит от температуры, увеличиваясь с ростом ее по следующему закону:

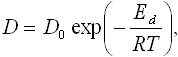
(5.6)

где D₀ - предэкспоненциальный множитель, E_d - энергия активации, R - универсальная газовая постоянная, T - температура.

Диффузную кривую для данного полимера можно представить по-разному, а именно:

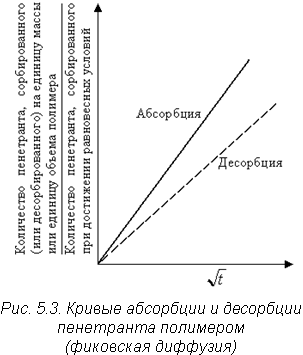
1. Кривой зависимости абсорбции (или десорбции) пенетранта от корня квадратного из времени диффузии (рис. 5.3).
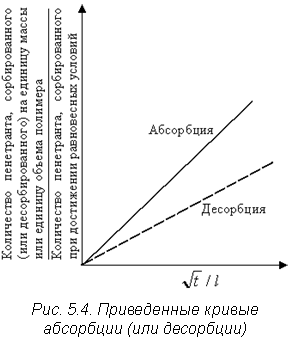
2. Кривой зависимости абсорбции (или десорбции) пенетранта от отношения корня квадратного из времени диффузии к толщине сухой полимерной пленки (l). Такую кривую (рис. 5.4) называют приведенной кривой абсорбции (или десорбции). Скорости абсорбции и десорбции одинаковы, поэтому какого-либо увеличения количества пенетранта или его потери не наблюдается.
3. Набором кривых абсорбции (или десорбции), снятых в идентичных экспериментальных условиях для пленок различной толщины, которые образуют одну кривую, если каждую из них представить в виде приведенной кривой абсорбции (или десорбции). Приведенная кривая десорбции всегда лежит между приведенной кривой абсорбции и осью приведенного времени при условии, что коэффициент диффузии увеличивается с концентрацией.

Диффузия молекул небольшого размера (органических жидкостей и паров) в полимерах происходит при переносе их из одной «дырки» в другую. С термодинамической точки зрения термин «дырка» означает вероятность образования центров сорбции для молекул пенетранта или диффузных каналов в полимере, через которые пенетрант может переходить из одного места в другое.

Фиковская диффузия подтверждается линейной зависимостью между абсорбцией (или десорбцией) пенетранта и корнем квадратным из времени диффузии.

На диффузионный процесс оказывают влияние следующие факторы:

1. Скорость диффузии уменьшается при понижении сегментальной подвижности, например из-за кристаллизации, повышения жесткости цепи или сшивания цепей. Модифицированный коэффициент диффузии для частично-кристаллической двухфазной (сферолитной) системы выглядит следующим образом

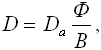
(5.7)

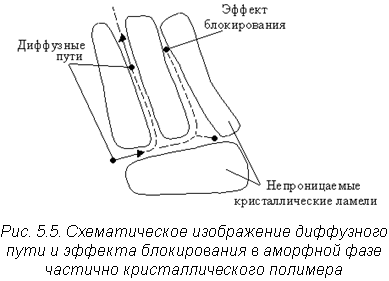
где D_a - коэффициент диффузии для полностью аморфного полимера, В - фактор блокирования, характеризующий блокирование диффузных путей через аморфные слои прилегающими непроницаемыми кристаллическими ламелями (рис. 5.5), Ф - фактор иммобилизации, характеризующий уменьшение подвижности цепи, обусловленное закреплением аморфных цепей между кристаллитами.

2. Факторы, которые способствуют увеличению фракционного свободного объема, например деформация. При упругой деформации в направлении, перпендикулярном кристаллической ламели, возрастают толщина и удельный объем аморфных слоев между ламелями.

3. Факторы, влияющие на процессы иммобилизации диффузанта в полимерной матрице.

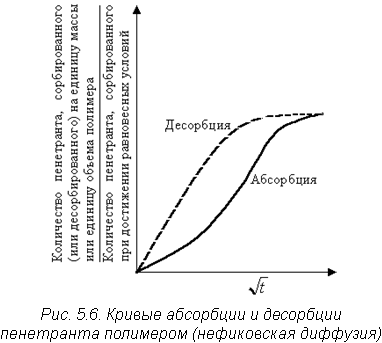
Нефиковская диффузия - это аномальное поведение, которое не удается описать в рамках законов Фика. Таким поведением могут характеризоваться полимеры при температурах, лежащих ниже температуры стеклования, а также сшитые и кристаллические полимеры при температурах выше температуры стеклования. Аномально-диффузное поведение проявляется в наличии существенных отклонений от линейной зависимости между абсорбцией пенетранта и корнем квадратным из времени диффузии (рис. 5.6). При нефиковской диффузии скорости абсорбции и десорбции не равны между собой.

Оба типа диффузии (фиковская и нефиковская) могут быть характерны для одного и того же полимера. Так некоторые пенетранты в данном полимере проявляют фиковское поведение, тогда как другие пенетранты показывают нефиковское поведение. При увеличении плотности сшивки в данном полимере диффузия имеет тенденцию переходить от фиковской к нефиковской.

Проницаемость газа через полимерную пленку можно представить как растворение газа или паров на одной поверхности пленки, диффундирование через пленку при градиенте концентрации и, наконец, испарение с другой поверхности при пониженной концентрации или пониженном давлении.

Если по толщине пленки разность давлений постоянная, то газ будет диффундировать через нее с постоянной скоростью в соответствии с первым законом Фика. При этом под потоком J понимают количество газа, диффундирующего через единицу поверхности пленки в единицу времени, выражая его при стандартных условиях (стандартных температуре и давлении - СТД). После интегрирования уравнения (5.4) по всей толщине пленки количество газа, продифундировавшего через полимерную пленку составляет

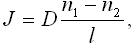
(5.8)

где n₁ и n₂ - концентрации газа на двух поверхностях.

Концентрацию газа обычно определяют исходя из давления (р) газа, находящегося в равновесии с пленкой. Согласно закону Генри (5.1)

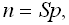
(5.9)

где n - концентрация газа в полимере, S - коэффициент растворимости газа в полимерной пленке, выражаемый при СТД в виде

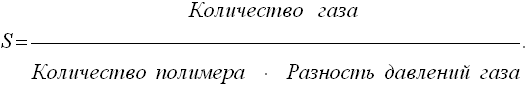
Отсюда

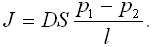
(5.10)

Коэффициент проницаемости (Р) определяется произведением

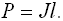
(5.11)

Параметры диффузии (D), проницаемости (P) и растворимости (S) зависят от температуры, концентрации, размера и формы молекул пенетранта, взаимодействия между полимером и диффузантом, морфологии и молекулярной подвижности полимера.