ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ
В результате первой стадии статистического исследования (статистического наблюдения) получают статистическую информацию,представляющую собой большое количество первичных, разрозненных сведений об отдельных единицах объекта исследования (записи о каждом гражданине страны при переписи населения: пол, национальность, возраст, образование, род занятий и многие другие признаки). Дальнейшая задача статистики заключается в том, чтобы привести эти материалы в определенный порядок, систематизировать и на этой основе дать сводную характеристику всей совокупности фактов при помощи обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности. Это достигается в результате группировки— второй стадии статистического исследования.
Статистическая группировка представляет собой процесс разделения сложного массового явления на однородные группы по каким-либо существенным признакам с целью выделения типов явлений, изучения структуры и анализа их состояния, развития и взаимосвязей.
Признак, положенный в основание группировки, называется группировочным признаком, или основанием группировки, и является отличительной чертой, свойственной единице статистической совокупности, на основе которой строятся отдельные группы.
Все признаки подразделяются на атрибутивные (качественные) и количественные. Атрибутивные, или качественные, признаки не имеют числового выражения имогут быть выражены только дискретными показателями в виде текстовой записи. Примерами качественных признаков могут быть: пол, национальность, образование, вид преступной деятельности, отрасль права и т.д. Количество возможных групп определяется числом исследуемых признаков
При группировке по количественному признаку, в отличие от качественного, каждая группа имеет числовое выражение и может принимать любые дробные и целочисленные значения, т.е. является непрерывно изменяющейся величиной. К таким группировочным признакам можно отнести, например, возраст, стаж работы, число зарегистрированных преступлений.
Кроме того, статистические группировки подразделяются на простые и комбинационные. В тех случаях, когда группировка осуществляется по одному признаку, она называется простой.
Комбинационными называют такие группировки, когда группировочный признак представлен в виде подгрупп. В зависимости от целей и задач наблюдения процесс формирования подгрупп может быть многоступенчатым.
В статистике группировки применяются для решения разнообразных задач, в зависимости от этого различают три вида группировок: типологические, аналитические и структурные
Типологическая группировкарешает задачу выявления и характеристики социально-экономических типов путем разделения качественно разнородной совокупности на классы, социально-экономические типы, однородные группы единиц в соответствии с правилами научной группировки.
Аналитические (факторные) группировкиисследуют связи и зависимостимежду изучаемыми явлениями и их признаками. В основе аналитической группировки лежит факторный признак, и каждая выделенная группа характеризуется средними значениями результативного признака.
Структурная группировка — это группировка, позволяющая выявить однородный (в качественном отношении) состав изучаемой статистической совокупности, т.е. определить структуру явления.
При группировке с непрерывно изменяющимися признаками границы группы указываются в интервалах. Интервал обозначает границы «от и до», в котором находится значение варьирующего признака. Различают равные и неравные интервалы. Величина (или ширина) интервала — это разность между его верхней и нижней границами. Величину равных интервалов определяют путем деления разности максимального и минимального значений признака на число образуемых групп. Количество образуемых групп определяется исходя из целей и задач проводимого исследования.
Приведем алгоритм построения равноинтервальной группировки по количественному признаку. Группировки с равными интервалами применяются в случае, когда степень вариации признака незначительна.
Группировку начинают с определения оптимального числа групп, на которую будет разбиваться изучаемая статистическая совокупность. Количество выделяемых групп зависит от степени вариации признака, положенного в основу группировки: чем она больше, тем большее число групп следует образовывать и тем точнее будет описан характер исследуемого объекта.
Для определения оптимального числа групп с равными интервалами пользуются формулой Стерджесса:
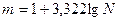
где N – объем совокупности;
m – число групп.
Данная формула применятся, как правило, для больших совокупностей (с объемом более 30 единиц). Для малых совокупностей число групп определяется исходя из целей и задач исследования.
После определения числа групп вычисляют ширину (величину) интервала h:
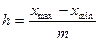
где 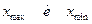 - соответственно максимальное и минимальное значение признака в совокупности. Результат вычисления округляют в большую сторону.
- соответственно максимальное и минимальное значение признака в совокупности. Результат вычисления округляют в большую сторону.
Далее определяют границы интервалов по формулам:
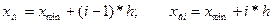
где 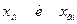 - соответственно нижняя и верхняя границы i-го интервала.
- соответственно нижняя и верхняя границы i-го интервала.
Завершают построение равноинтервальной группировки подсчетом числа единиц совокупности, попавших в каждый интервал и построением группировочной таблицы.
Пример 2.1. На основе данных о возрасте лиц, совершивших административные правонарушения, построить равноинтервальную группировку:
20 18 16 14 15 19 45 15 49 22 35 27 26 40 39 26 24 23 29 27 27 17 15 38 28 20 18 29 19 25 34 29 20 22 23 15 19 40 17 19 16 33 27 19 14 25 26 33 14 27.
.
Решение.
Определяем оптимальное число групп:
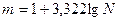
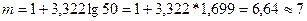
Вычисляем величину интервала:
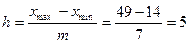
Находим границы интервалов по группам:
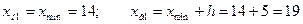
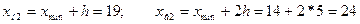
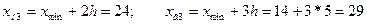
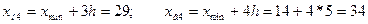
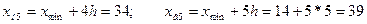
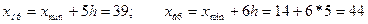
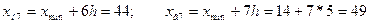
Подсчитываем число единиц совокупности, попавших в каждую группу и оформляем результаты группировки в виде группировочной таблицы (таблица 2.1). Необходимо отметить, что в этом распределении имеет место неоднозначность: к какой группе отнести, например, преступника в возрасте 19 лет, к первой или ко второй? Для устранения этой неопределенности необходимо применить принцип единообразия (например, нижняя граница интервала включает в себя рассматриваемое значение, а верхняя – не включает). Исходя из этого принципа, лицо в возрасте 19 лет должно быть отнесено ко второй группе.
Таблица 2.1
| Номер группы | Возраст лиц, совершивших правонарушения, лет | Число лиц, совершивших правонарушения, чел |
| 14-19 | ||
| 19-24 | ||
| 24-29 | ||
| 29-34 | ||
| 34-39 | ||
| 39-44 | ||
| 44-49 |
При получении групп, наиболее адекватно отражающих реальность, необходимо руководствоваться сущностью изучаемого явления. В этом случае интервалы могут быть и неравными. Так, при исследовании некоторых явлений могут использоваться прогрессивно возрастающие или убывающие интервалы. Так же неравные интервалы образуются и при построении группировок с равнонаполненными группами (численность единиц одинакова для всех групп). Остановимся на построении такого вида группировок.
На первом этапе так же, как и при построении равноинтервальных группировок определяют оптимальное число групп m, используя формулу Стерджесса или исходя из логических соображений и целей исследования.
Второй шаг предусматривает определение численности каждой группы путем деления объема совокупности N на число групп m:
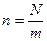
Если в результате вычисления получается нецелое число, то в этом случае число единиц в отдельных группах будет неодинаковым.
На следующем этапе определяют границы интервалов. При этом должны выполняться следующие требования: интервалы должны быть смежными (нижняя граница последующего интервала должна совпадать с верхней границей предыдущего интервала; единицы с одним и тем же значениям признака должны быть отнесены к одной и той же группе. Поэтому численность некоторых групп может различаться.
Пример 2.2. Построить группировку с равнонаполненными группами по данным о нарушении скоростного режима на автомобильных дорогах района (в км/ч):
168 115 137 124 145 105 135 125 122 146 170 135 100 132 150 110 105 127 118 112 130 155 138 128 142 100 130 150 135 180 120 145 125 140 175
.
Решение.
Определяем оптимальное число групп:
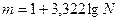
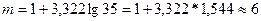
Вычисляем численность каждой группы:
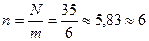
Для определения границ интервалов и распределения единиц совокупность по группам упорядочим совокупность по возрастанию значений группировочного признака и распределим единицы по группам следующим образом: первые 6 единиц будут отнесены к первой группе, следующие 6 единиц ко второй группе и т.д. Поскольку объем совокупности равен 35 единицам, то в последнюю шестую группу войдут только 5 единиц (таблица 2.2).
Таблица 2.2
| Скорость, км/ч | |||||||||||||
| Номер группы | |||||||||||||
| Скорость, км/ч | |||||||||||||
| Номер группы | |||||||||||||
| Скорость, км/ч | |||||||||||||
| Номер группы |
Используя данные таблицы 2.2, определяем границы интервалов и составляем таблицу равнонаполненной группировки (таблица 2.3):
Таблица 2.3
| Номер группы | Скорость, км/час | Число лиц, нарушивших скоростной режим, чел |
| 100-115 | ||
| 115-125 | ||
| 125-135 | ||
| 135-142 | ||
| 142-155 | ||
| 155-180 |
Данные виды группировок являются простыми, в их основе лежит один группировочный признак. На их основе могут формироваться сложные группировки, выполняемые по двум и более признакам. Сложные группировки отражают разнородность изучаемых явлений, когда последние имеют несколько противоречивых тенденций динамики и распределения. Наиболее распространены комбинационные группировки, которые помогают решать задачи выделения типов изучаемых явлений, выявления структурных сдвигов и взаимосвязей.
Комбинационная группировка – группировка по нескольким признакам, осуществляемая последовательно. Последовательность устанавливается исходя из логики взаимосвязи показателей. Обычно начинают группировку с атрибутивного признака. При построении данного вида группировки группы, образованные по одному признаку, делятся на подгруппы по второму, затем по третьему признаку и т.д. Оптимальное число признаков – два-четыре, так как применение большого числа группировочных признаков снижает наглядность, затушевывает проявление закономерностей.
Комбинационная группировка по двум признакам (X, Y) оформляется в виде комбинационной таблицы, в которой значения признака Х откладываются по строкам, а значения признака Y по столбцам. Значения признаков X и Y являются результатом выполнения простых группировок по данным признакам. В теле комбинационной таблицы содержатся частоты совместного появления значений признаков X и Y. Приведем пример построения комбинационной группировки по двум признакам:
Пример 2.3.Построить комбинационную группировкупо двум признакам (таблица 2.4): количеству административных правонарушений и поступлениям в бюджет от уплаты штрафов и выявить, взаимосвязаны ли эти два признака между собой.
Таблица 2.4
| № муниципального подразделения | Число административных правонарушений | Поступления в бюджет от уплаты штрафов, тыс. руб. |
| 15,7 | ||
| 18,0 | ||
| 12,1 | ||
| 13,8 | ||
| 15,5 | ||
| 17,9 | ||
| 12,8 | ||
| 14,2 | ||
| 15,9 | ||
| 17,6 | ||
| 18,2 | ||
| 13,0 | ||
| 16,5 | ||
| 16,2 | ||
| 16,7 | ||
| 14,6 | ||
| 14,8 | ||
| 16,1 | ||
| 16,7 | ||
| 15,8 |
Решение.
Воспользуемся результатами равнонаполненной группировки по признаку X (число административных правонарушений) и равноинтервальной группировки по признаку Y (поступления в бюджет от уплаты штрафов, тыс. руб.), полученных аналогично представленным выше примерам. В комбинационной таблице по строкам откладываются значения признака X, по столбцам – значения признака Y, представленные в виде интервалов – таблица 2.5. На пересечении столбцов и строк в теле таблицы находятся частоты совместного проявления значения признаков X и Y.
Таблица 2.5
| Поступления в бюджет, тыс. руб.,Y | 12,1-13,7 | 13,7-15,3 | 15,3-16,9 | 16,9-18,5 | Итого |
| Количество правонарушений, X | |||||
| 41-57 | - | - | |||
| 57-67 | - | - | |||
| 67-80 | - | - | |||
| 80-92 | - | - | |||
| Итого: |
Анализируя комбинационную группировку, можно сделать вывод о направлении связи между признаками. Если максимальные частоты располагаются вблизи главной диагонали (проходящей из левого верхнего угла в правый нижний угол), то связь между признаками прямая. Если максимальные частоты располагаются вблизи побочной диагонали (проходящей из правого верхнего угла в левый нижний угол), то связь - обратная. Если максимальные частоты располагаются хаотично (невозможно определить к какой диагонали они соответствуют), то связи нет. В нашем примере связь между признаками прямая, так как максимальные частоты находятся вдоль главной диагонали (выделено жирным шрифтом).
Контрольные вопросы
1. Понятие статистической группировки.
2. Виды группировок. Их краткая характеристика.
3. Задачи, решаемые статистикой с помощью статистических группировок.
4. Типологические, структурные и аналитические группировки, их взаимосвязь.
5. Простые и сложные группировки, преимущества и недостатки.
6. Порядок построения группировки с равными интервалами.
7. Построение равнонаполненной группировки.
8. Порядок выполнения комбинационной группировки.
Задачи
Задача 1. К какому виду группировочных признаков (качественным или количественным) относятся следующие признаки: а) пол осужденного; б) возраст осужденного; в) национальность; г) стаж работы следователя; д) срок лишения свободы; е) уровень дохода; ж) гражданство; з) численность работников прокуратуры.
Задача 2. Имеются следующие данные о степени выполнения норм выработки рабочими-осужденными цеха в колонии строгого режима за октябрь текущего года, в %:
95,4; 99,3; 130,2; 120,1; 119,4; 98,8; 129,0; 103,2;103,6; 100,5; 150,5; 140,3; 109,2; 99,5; 97,8; 168,0; 101,2; 115,8; 90,6; 103,4; 190,3; 202,0; 105,0; 150,0; 96,8; 160,3; 130,0; 119,6; 110,8; 111,5; 90,3; 99,2; 99,0; 127,0; 170,4; 99,9; 116,5; 130,4; 125,4; 89,8.
Постройте равноинтервальную группировку осужденных по степени выполнения норм выработки, выделив четыре группы рабочих-осужденных с равными интервалами.
Задача 3. По данным УМВД зарегистрировано преступлений, совершенных в несовершеннолетними в возрасте:
17 13 15 16 17 15 15 14 16 13 14 17 14 15 15 16 16 15 14 15 15 14 16 16 14 17 16 15 16 15 13 15 15 13 15 14 15 13 17 14.
Постройте равнонаполненную группировку несовершеннолетних по возрасту, выделив пять групп.
Задача 4. По данным об объеме производства алкогольной продукции и числе зарегистрированных случаев разбоя построить комбинационную группировку, по результатам группировки сделать выводы о взаимосвязи признаков.
| Объем производства алкогольной продукции, млн. руб. | |||||||||
| Число зарегистрированных случаев разбоя |
| Объем производства алкогольной продукции, млн. руб. | |||||||||
| Число зарегистрированных случаев разбоя |
Дата добавления: 2020-11-18; просмотров: 1148;











