Закрепление нового материала.

Повторение свойств степени.

Перечислим свойства показателей степени:

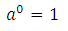
Нулевая степень любого числа равна единице.

Далее:

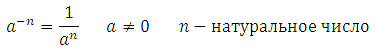
Следствие из данного свойства:

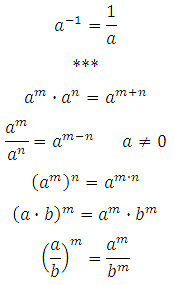
2. Объяснение нового материала.

Показательным уравнением называется уравнение содержащее переменную в показателе, то есть это уравнение вида:

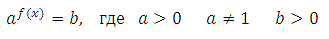, где f(x) выражение, которое содержит переменную.

Методы решения показательных уравнений

1. В результате преобразований уравнение можно привести к виду:

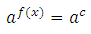
Тогда применяем свойство:

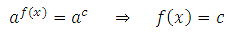
2. При получении уравнения вида a ^f(x)=b используется определение логарифма, получим:

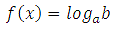
3. В результате преобразований можно получить уравнение вида:

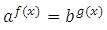
Применяется логарифмирование:

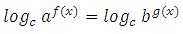
Далее применяем свойство логарифма степени:

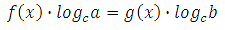
Выражаем и находим х.

Закрепление нового материала.

1. Найдите корень уравнения:

4^1–2х = 64.

Необходимо сделать так, чтобы в левой и правой частях были показательные выражения с одним основанием. 64 мы можем представить как 4 в степени 3. Получим:

4^1–2х = 4³

Основания равны, можем приравнять показатели:

1 – 2х = 3

– 2х = 2

х = – 1

Проверка:

4^1–2(–1) = 64

4¹⁺² = 64

4³ = 64

64 = 64

Ответ: –1

2. Найдите корень уравнения 3^х–18 = 1/9.

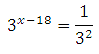
Известно, что

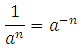
Значит 3^х-18 = 3^-2

Основания равны, можем приравнять показатели:

х – 18 = – 2

х = 16

Проверка:

3^16–18 = 1/9

3^–2 = 1/9

1/9 = 1/9

Ответ: 16

3. Найдите корень уравнения:

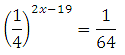
Представим дробь 1/64 как одну четвёртую в третьей степени:

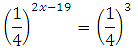
Теперь можем приравнять показатели:

2х – 19 = 3

2х = 22

х = 11

Проверка:

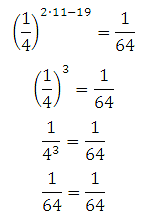
Ответ: 11