Образование лиофильных коллоидных систем
Многие коллоидные системы могут возникать спонтанно, или самопроизвольно. Эти системы называются лиофильными коллоидными системами, так как взаимодействие между веществом дисперсной фазы и средой достаточно большое.
Образование термодинамически устойчивых дисперсных систем, как и истинных растворов, происходит самопроизвольно, сопровождаясь уменьшением свободной энергии.
Изменение свободной энергии при самопроизвольном диспергировании может быть выражено следующим образом:
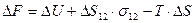 (7.15)
(7.15)
При добавлении объем системы не меняется и 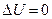 . Поверхность при диспергировании увеличивается, т.е.
. Поверхность при диспергировании увеличивается, т.е. 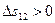 . Энтропия системы при дроблении также возрастает:
. Энтропия системы при дроблении также возрастает: 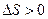 .
.
Для самопроизвольного протекания процесса должно выполняться условие 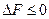 . Это условие будет выполнимо, если возрастание свободной энергии из-за увеличения поверхности при диспергировании будет меньше убыли свободной энергии из-за возрастания энтропии:
. Это условие будет выполнимо, если возрастание свободной энергии из-за увеличения поверхности при диспергировании будет меньше убыли свободной энергии из-за возрастания энтропии:
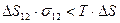 (7.16)
(7.16)
Изменение поверхности пропорционально числу частиц n, умноженному на размер частиц в квадрате 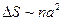 . Изменение энтропии
. Изменение энтропии 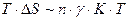 , т.е. кинетической энергии частиц, где
, т.е. кинетической энергии частиц, где 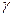 - безмерный коэффициент, равный ~ 30.
- безмерный коэффициент, равный ~ 30.
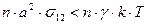 (7.17)
(7.17)
Из этого уравнения можно получить критическое значения поверхностного натяжения:
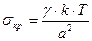 (7.18)
(7.18)
для частиц 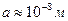 ,
, 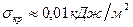 .
.
Самопроизвольное диспергирование возможно для коллоидных систем, в которых 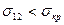 .
.
Несмотря на большую межфазную поверхность в лиофильных дисперсных системах, малое межфазное натяжение обуславливает сравнительно небольшую поверхностную энергию, которая способна компенсироваться энтропийной составляющей. Малое значение 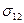 возможно только при значительном межфазном взаимодействии, характерном для жидких сред. Поэтому термодинамически устойчивыми свободно-дисперсионными системами могут быть только системы с жидкой дисперсной средой.
возможно только при значительном межфазном взаимодействии, характерном для жидких сред. Поэтому термодинамически устойчивыми свободно-дисперсионными системами могут быть только системы с жидкой дисперсной средой.
При самопроизвольном диспергировании образуются дисперсные системы, характеризующиеся кривыми распределения с некоторым наиболее вероятным радиусом, т. е. существует оптимальная дисперсность. Дальнейшее диспергирование, вплоть до молекул, невозможно, так как состояние с оптимальной дисперсностью более выгодно, чем состояние двух сопряженных сплошных фаз или состояние истинного раствора. По мнению Ребиндера, термодинамическая устойчивость двухфазных дисперсных систем определяется двумя условиями: достаточно низким межфазным поверхностным натяжением и быстрым его ростом с уменьшением радиуса частиц.
Наиболее типичными представителями лиофильных коллоидных систем являются растворы коллоидных ПАВ и высокомолекулярных соединений, а также водные дисперсии эмульсолов (углеводородов с большим содержанием (10-20%) мыл или мылоподобных поверхностно-активных веществ). Эмульсолы применяют в качестве смазочно-охлаждающих жидкостей (СОЖ) при холодной обработке металлов.
VIII. Молекулярно-кинетические свойства коллоидных систем
Введение
Молекулярно-кинетическая теория изучает законы самопроизвольного движения молекул и частиц. Причинами самопроизвольного движения частиц являются тепловое движение молекул окружающей среды или действие сил тяжести. Тепловое движение на микроуровне проявляется в форме броуновского движения, а на макроуровне - в форме диффузии или осмоса. Сила тяжести или центробежная сила является движущей силой при седиментации частиц. Коллоидные частицы по размерам занимают промежуточное положение между грубодисперсными частицами и молекулами. Они доступны для наблюдения, и в то же время настолько малы, что участвуют в тепловом движении. Это следует из основного положения кинетической теории, заключающегося в том, что при отсутствии внешних сил все частицы, независимо от их размера, имеют одинаковую среднюю кинетическую энергию, равную 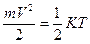 . Другими словами, с уменьшением массы частицы ее средняя скорость увеличивается.
. Другими словами, с уменьшением массы частицы ее средняя скорость увеличивается.
Молекулярно-кинетические свойства коллоидных систем описываются теми же закономерностями, что и молекулярные растворы, но выражены слабее, т.к. численная концентрация коллоидных растворов ниже, чем молекулярных. На молекулярно-кинетических свойствах основаны некоторые методы определения массы частиц, в частности ультрацентрифугирование.
8.2. Броуновское движение
8.2.1. Природа броуновского движения
В 1827 году английский ботаник Броун обнаружил с помощью микроскопа движение мелких частиц - спор папоротника, взвешенных в воде. Более крупные частицы находились в колебательном движении. Колебания и перемещения частиц ускорялись с уменьшением размера частиц, повышением температуры и не были связаны с какими-либо внешними условиями. Оказалось, что причиной броуновского движения являются не внешние факторы, а внутренние, присущие самой системе. Объяснение броуновского движения было дано Гуи только через 60 лет после его открытия (1888 год), а строгая теория создана Эйнштейном (1905 год) и Смолуховским (1906 год) позднее. Правильность этой теории была доказана многочисленными экспериментами.
Природа броуновского движения состоит в том, что молекулы среды (жидкости или газа) сталкиваются с частицей дисперсной фазы,в результате чего она получает громадное число ударов с разных сторон. Если частица имеет большие размеры, то число этих ударов так велико, что вследствие статистического закона импульсы взаимно компенсируются, и результирующий импульс равен нулю. Такая частица будет неподвижной еще и потому, что она обладает большой инерционностью и мало чувствительна к ударам молекул с малой энергией. Если частица мала, то возрастает вероятность того, что число или интенсивность ударов молекул с одной стороны будут больше, чем с другой. Результирующая сила вызовет смещение частицы. Движение частицы указывает на тепловое движение молекул среды, так же, как качка корабля на море указывает на существование волн. В броуновском движении участвуют частицы с размером менее 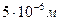 .
.
8.2.2. Общенаучное значение броуновского движения
Теория броуновского движения сыграла громадную роль в науке. Теоретическое обоснование тепловой природы броуновского движения явилось доказательством реальности существования молекул, отрицаемых Махом и Вильгельмом Отсвальдом. В связи с этим теория броуновского движения убедительно склонила чашу весов в пользу материалистического мировоззрения.
С помощью броуновского движения доказывается статистический характер второго закона термодинамики. В результате броуновского движения возникают флуктуации концентрации на молекулярном уровне или уровне малых частиц. Когда коллоидная частица самопроизвольно поднимается в броуновском движении, потенциальная энергия системы возрастает. При опускании частицы вниз за счет возросшей потенциальной энергии можно совершить работу. Следовательно, теплота окружающей среды превращается в работу в отсутствие начальной разности температур, то есть мы приходим к неверному выводу о том, что действует вечный двигатель второго рода. Ошибочность подобного заключения состоит в том, что подобная схема применима к отдельной частице, но не применима к множеству частиц. Согласно теории вероятностей, при большом числе частиц, если одна частица движется вверх, приводя к увеличению потенциальной энергии, то всегда найдется другая частица, двигающаяся вниз, и потенциальная энергия не изменится. Таким образом, второе начало термодинамики не применимо к отдельной частице, так как оно является вероятностным законом. Так броуновское движение привело к доказательству статистического характера второго закона термодинамики.
8.2.3. Средний сдвиг частицы
Броуновское движение привлекло внимание выдающихся физиков-теоретиков и прежде всего Эйнштейна, создавшего в 1905 году статистическую теорию броуновского движения. Основным постулатом этой теории является полная хаотичность движения, то есть рассмотрение движения частицы как «случайного блуждания» в трех измерениях. Частица 1020 раз в секунду изменяет направление движения. Истинный путь движения частицы определить невозможно, но можно определить среднее расстояние, на которое она смещается. На рис.8.1 представлена проекция траектории движения частицы на плоскость.
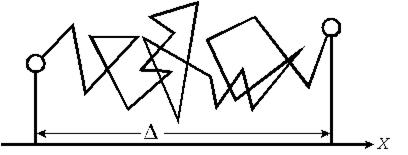
Рис. 8.1. Проекция траектории движения частицы на плоскость
Для количественных расчетов применяют среднеквадратичное значение проекции смещения частицы:
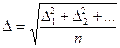 , (8.1)
, (8.1)
где n - число отдельных проекций. Среднеарифметическое значение проекции смещения равно нулю, так как все направления движения равновероятны.
8.3. Диффузия
Броуновское движение является причиной диффузии в коллоидных системах. Диффузией называется самопроизвольный процесс переноса вещества. приводящий к выравниванию концентраций и химического потенциала в результате теплового движения молекул, ионов и частиц. Диффузия идет вследствие тенденции молекул мигрировать из области высоких концентраций в область низких концентраций. Диффузия является необратимым процессом, сопровождающимся ростом энтропии, так как он переводит систему в наиболее неупорядоченное состояние. В однокомпонентной системе говорят о самодиффузии вследствие теплового движения частиц или молекул. В многокомпонентных системах говорят о взаимодиффузии, приводящей к выравниванию концентраций.
8.3.1. Выражения для идеальной диффузии. Первый и второй законы Фика
Диффузия описывается законами Фика. По аналогии с переносом тепла Фик установил, что перенос массы в соответствии с общей теорией потоков описывается уравнением
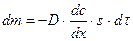 , (8.2)
, (8.2)
где 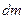 - количество продиффундировавшего вещества,
- количество продиффундировавшего вещества, 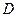 - коэффициент диффузии,
- коэффициент диффузии, 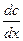 - градиент концентрации,
- градиент концентрации, 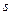 - площадь, через которую идет диффузия,
- площадь, через которую идет диффузия, 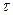 - время. Знак «минус» перед правой частью уравнения стоит потому, что с увеличением
- время. Знак «минус» перед правой частью уравнения стоит потому, что с увеличением 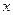 величина
величина 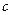 уменьшается, и производная
уменьшается, и производная 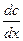 отрицательна. Первый закон Фика характеризует стационарный процесс диффузии. Стационарным называется процесс, который зависит только от разности аргументов. Возьмем ряд расстояний
отрицательна. Первый закон Фика характеризует стационарный процесс диффузии. Стационарным называется процесс, который зависит только от разности аргументов. Возьмем ряд расстояний 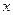 , которым соответствуют значения концентрации
, которым соответствуют значения концентрации 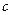 :
:
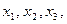 …………………
………………… 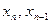
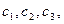 …………………
………………… 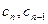
Для стационарного процесса разность последующего и предыдущего значений 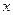 и
и 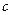 постоянна для всего ряда:
постоянна для всего ряда:
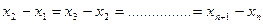
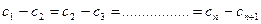
Когда градиент концентрации постоянен, можно записать:
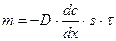 (8.3)
(8.3)
При 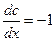 ,
, 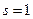 ,
, 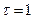 ,
, 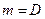 , то есть коэффициент диффузии численно равен количеству вещества, продиффундировавшего через единицу площади в единицу времени при градиенте концентрации, равном единице.
, то есть коэффициент диффузии численно равен количеству вещества, продиффундировавшего через единицу площади в единицу времени при градиенте концентрации, равном единице.
Размерность коэффициента диффузии получается из выражения (8.3)
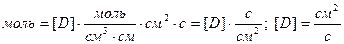
Исходя из первого закона Фика, при 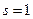 и
и 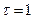
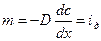
Величина 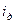 называется потоком диффузии.
называется потоком диффузии.
Коэффициент диффузии для газов или веществ, слабо взаимодействующих со средой, в которой происходит диффузия, не зависит от концентрации.
Второй закон Фика характеризует нестационарный процесс диффузии и описывает накопление вещества в различных точках пространства в зависимости от времени поглощения вещества твердым телом, то есть сорбцию:
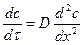 (8.4)
(8.4)
Зависимость коэффициента диффузии от температуры выражается уравнением типа уравнения Аррениуса:
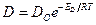 (8.5)
(8.5)
где ED - энергия активации диффузии.
8.3.2. Градиент концентрации при диффузии
Рассмотрим распределение вещества в пространстве и времени при диффузии (рис. 8.2).
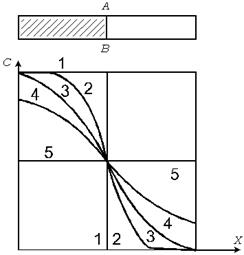
Рис. 8.2. Изменение концентрационного профиля при диффузии за время от t=0 (кривая 1) до t=¥ (кривая 5).
Пусть раствор с концентрацией 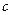 отделен от чистого растворителя перегородкой. Удалим перегородку и рассмотрим изменение концентрации в процессе диффузии в различные моменты времени
отделен от чистого растворителя перегородкой. Удалим перегородку и рассмотрим изменение концентрации в процессе диффузии в различные моменты времени 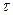 . Кривые, характеризующие концентрационный профиль вещества, пересекаются в одной точке и симметричны. Наибольшие изменения концентрации во времени происходят вблизи начальной границы раздела, то есть при наибольшем градиенте
. Кривые, характеризующие концентрационный профиль вещества, пересекаются в одной точке и симметричны. Наибольшие изменения концентрации во времени происходят вблизи начальной границы раздела, то есть при наибольшем градиенте 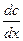 .
.
8.3.3. Диффузия и проницаемость
Из законов Фика можно получить выражение для неравновесной концентрации в полубесконечном теле на расстоянии 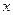 при времени диффузии, равном
при времени диффузии, равном 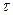 . Тело считается полубесконечным, если за время эксперимента фронт диффундирующего вещества не достигает границ (см. рис. 8.2).
. Тело считается полубесконечным, если за время эксперимента фронт диффундирующего вещества не достигает границ (см. рис. 8.2).
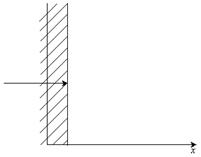
Рис. 8.3.
Выражение для неравновесной концентрации имеет вид:
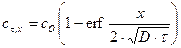 , (8.6)
, (8.6)
erf - функция ошибок Гаусса
Количество поглощенного вещества равно
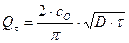 (8.7)
(8.7)
К процессам массопереноса, определяемым диффузией, кроме сорбции, относится также массопроницаемость. Схемы сорбции и проницаемости изображены на рис. 8.4.
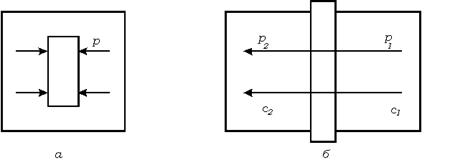
Рис. 8.4. Схеа сорбции ( 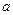 ) и проницаемости (б).
) и проницаемости (б).
Маcсопроницаемостью называется перенос вещества через мембрану за счет разности концентраций или давлений с обеих сторон мембраны. Проницаемость характеризуется коэффициентом проницаемости 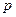 , равным количеству диффундирующего вещества, проходящего через 1 см3 вещества мембраны при разности давлений 1 атм за 1 с.
, равным количеству диффундирующего вещества, проходящего через 1 см3 вещества мембраны при разности давлений 1 атм за 1 с.
Поток вещества равен
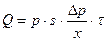 , (8.8)
, (8.8)
где 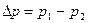 ,
, 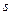 - площадь мембраны,
- площадь мембраны, 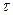 - время.
- время.
Если перенос вещества происходит вследствие разности концентраций, то поток вещества выражается формулой
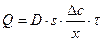 , (8.9)
, (8.9)
где 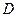 - коэффициент диффузии,
- коэффициент диффузии, 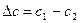 .
.
Существуют два механизма переноса: диффузионный, когда вещество переносится в виде раствора и не образует отдельной фазы, и фазовый, когда вещество образует отдельную фазу. В последнем случае перенос происходит по порам и дефектам. При фазовом переносе различают поток Кнудсена, осуществляемый при малых давлениях и малых размерах пор. Этот тип переноса наблюдается при условии, что длина свободного пробега молекул l больше диаметра поры d (l>d). Молекулы сталкиваются со стенками поры и не сталкиваются друг с другом, так как давление мало. Вторым типом фазового переноса является ламинарный поток Пуайзеля, наблюдаемый при условии (l<d). При этом молекулы газа проходят через пору, не сталкиваясь со стенкой. При дальнейшем увеличении диаметра пор проницаемость определяется истечением газов из отверстий. При промежуточных давлениях осуществляются оба типа фазового переноса. Для реальных пористых тел наблюдается смешанный (диффузионный и фазовый) перенос.
8.4. Седиментация и методы седиментационного анализа
При рассмотрении диффузии мы не учитывали влияния гравитационного поля. Когда масса частиц достаточно велика, происходит оседание частиц дисперсной фазы, называемое седиментацией. Для более мелких частиц в системе устанавливается равновесное распределение частиц по высоте. Способность дисперсной системы сохранять постоянное распределение частиц по объему называют седиментационной устойчивостью.
8.4.1. Гипсометрический закон
Влияние теплового движения и гравитационного поля на распределение частиц можно рассмотреть количественно.
В соответствии с первым законом Фика поток диффузии 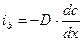 . Поток седиментации
. Поток седиментации 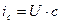 , где
, где 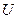 - скорость седиментации,
- скорость седиментации, 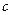 - концентрация.
- концентрация.
При равномерном оседании вес частицы 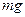 уравновешивается силой трения
уравновешивается силой трения 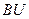 (
( 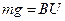 ), где
), где 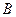 - коэффициент трения. Отсюда:
- коэффициент трения. Отсюда:
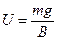 ,
, 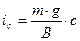 . (8.10)
. (8.10)
Если соотношение 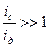 , то системы грубо дисперсны, седиментационно неустойчивы, диффузию для них можно не принимать во внимание. Если
, то системы грубо дисперсны, седиментационно неустойчивы, диффузию для них можно не принимать во внимание. Если 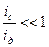 , то системы обладают высокой седиментационной устойчивостью. В расчет можно принимать только диффузию, а седиментация ничтожна. Такое положение характерно для истинных растворов. Если
, то системы обладают высокой седиментационной устойчивостью. В расчет можно принимать только диффузию, а седиментация ничтожна. Такое положение характерно для истинных растворов. Если 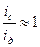 , то есть
, то есть 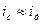 , то следует учитывать оба процесса: седиментацию и диффузию, при этом устанавливается равновесное распределение частиц дисперсной фазы по высоте. Такое положение характерно для коллоидных систем и растворов высокомолекулярных соединений.
, то следует учитывать оба процесса: седиментацию и диффузию, при этом устанавливается равновесное распределение частиц дисперсной фазы по высоте. Такое положение характерно для коллоидных систем и растворов высокомолекулярных соединений.
При условии равновесия 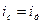 :
:
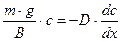 ;
; 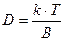 ;
;
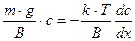 ;
; 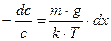
Так как градиент концентрации изменяется по высоте, то 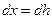 . После интегрирования от
. После интегрирования от 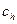 до
до 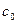 и от нуля до
и от нуля до 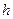 получим:
получим:
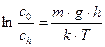 ;
; 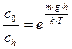 ;
; 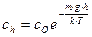 (8.11)
(8.11)
Это частный случай распределения молекул по Больцману.
Если значение 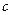 заменить пропорциональным ей значением
заменить пропорциональным ей значением 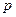 , получим:
, получим:
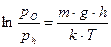 или
или 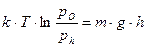 (8.12)
(8.12)
Это выражение известно под названием гипсометрического закона, определяющего распределение молекул газа по высоте (Gypsos-высота (лат)). Согласно формуле (8.12), давление воздуха на высоте 6 км уменьшается вдвое. Левая часть уравнения (8.12) представляет собой работу обратимого изотермического расширения моля газа от давления 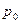 до давления
до давления 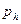 . Правая часть уравнения является работой поднятия моля газа на высоту
. Правая часть уравнения является работой поднятия моля газа на высоту 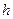 .
.
Таким образом, 1 моль газа можно перевести от давления 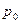 до давления
до давления 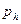 двумя способами: изотермически и обратимо расширить от давления
двумя способами: изотермически и обратимо расширить от давления 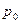 до
до 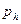 или поднять от поверхности земли на высоту
или поднять от поверхности земли на высоту 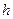 . Такое же действие можно осуществить с коллоидным раствором. Если в длинную трубку поместить раствор, то концентрация частиц у поверхности земли будет равна
. Такое же действие можно осуществить с коллоидным раствором. Если в длинную трубку поместить раствор, то концентрация частиц у поверхности земли будет равна 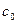 , а на высоте
, а на высоте 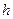 концентрация будет меньше и равна
концентрация будет меньше и равна 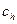 ;
; 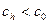 . Работа переноса одного моля вещества от концентрации
. Работа переноса одного моля вещества от концентрации 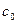 к концентрации
к концентрации 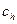 равна работе поднятия одного моля вещества на высоту
равна работе поднятия одного моля вещества на высоту 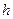 .
.
Гипсометрический закон для золей записывается в следующем виде:
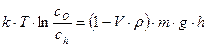 , (8.13)
, (8.13)
где 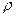 - плотность,
- плотность, 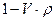 - поправка на плавучесть.
- поправка на плавучесть.
Для получения ощутимых разностей концентраций и определения массы частицы по уравнению (8.13) необходимы настолько длинные трубки (высотой 2÷3 км), что применять их не имеет смысла. Поэтому идут по другому пути, а именно, увеличивают не высоту в уравнении (8.13), а ускорение 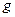 , применяя ускорения, в сотни тысяч раз большие ускорения силы тяжести. Это стало возможным благодаря применению ультрацентрифуги.
, применяя ускорения, в сотни тысяч раз большие ускорения силы тяжести. Это стало возможным благодаря применению ультрацентрифуги.
Гипсометрический закон достаточно точно соблюдается для лиозолей. Так, Перрен микроскопически определил равновесное распределение частиц гуммигута по высоте и рассчитал значение числа Авогадро, которое оказалось близким к значению, определенному другими методами.
8.4.2. Седиментационное уравнение незаряженной частицы
Рассмотрим седиментацию незаряженной частицы, масса которой равна 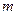 , а объем -
, а объем - 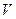 , в жидкости плотностью
, в жидкости плотностью 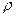 . На частицу действуют направленные в разные стороны сила тяжести
. На частицу действуют направленные в разные стороны сила тяжести 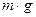 и сила Архимеда
и сила Архимеда 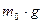 , где
, где 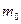 - масса жидкости в объеме частицы, равная
- масса жидкости в объеме частицы, равная 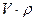 . Седиментационная сила, которая не зависит от формы частицы, равна их разности:
. Седиментационная сила, которая не зависит от формы частицы, равна их разности:
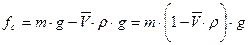 (8.14)
(8.14)
где 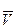 - удельный объем частицы.
- удельный объем частицы.
При оседании частицы действует сила трения, равная 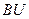 , где
, где 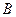 - коэффициент трения,
- коэффициент трения, 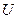 - скорость седиментации.
- скорость седиментации.
При стационарном режиме оседания седиментационная сила уравновешивается силой трения.
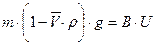 (8.15)
(8.15)
По уравнению (8.15) можно определить массу частицы, но это требует знания коэффициента трения.
8.4.3. Ультрацентрифуга
Под действием силы тяжести оседают только крупные частицы. Коллоидные частицы оседают чрезвычайно медленно. Так, частицы кварца (r=1×10-7 м) проходят путь в 1 см за 86 ч. Поэтому для ускорения седиментации заменяют гравитационное поле центробежным, применяя ультрацентрифуги, дающие мощное силовое поле. Ускорения, создаваемые ультрацентрифугой, достигают 105 g, а число оборотов - 75 тыс. об/мин. При таких ускорениях та же частица кварца проходит путь в 1 см за 3 с.
Существуют два метода определения размеров частиц с использованием ультрацентрифуги: скоростное ультрацентрифугирование и равновесное ультрацентрифугирование.
8.4.4. Скоростное ультрацентрифугирование
В методе скоростного ультрацентрифугирования применяются центробежные ускорения порядка 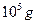 . При центрифугировании частица, удаляясь от оси вращения, двигается со все возрастающей скоростью. Поэтому величину
. При центрифугировании частица, удаляясь от оси вращения, двигается со все возрастающей скоростью. Поэтому величину 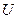 в седиментационном уравнении следует заменить на
в седиментационном уравнении следует заменить на 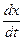 , где
, где 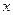 - расстояние частицы от оси вращения,
- расстояние частицы от оси вращения, 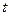 - время. Центробежное ускорение равно
- время. Центробежное ускорение равно 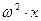 , где
, где 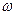 - угловая скорость вращения. Тогда седиментационное уравнение принимает вид:
- угловая скорость вращения. Тогда седиментационное уравнение принимает вид:
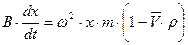 ;
; 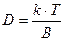 ;
; 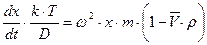 (8.16)
(8.16)
В качестве величины, зависящей только от размера и плотности частиц, вводят отношение скорости оседания частицы к центробежному ускорению, то есть величину 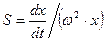 , которую называют константой седиментации. Тогда
, которую называют константой седиментации. Тогда
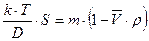 ;
; 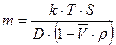 (8.17)
(8.17)
Скорость оседания частицы очень мала, а угловая скорость вращения ротора велика. Поэтому абсолютные значения 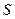 столь малы, что для ее измерения ввели специальную единицу, называемую сведбергом, в честь шведского исследователя. 1 сведберг = 10-13 с. Величина
столь малы, что для ее измерения ввели специальную единицу, называемую сведбергом, в честь шведского исследователя. 1 сведберг = 10-13 с. Величина 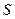 является характеристической константой частицы. Значение
является характеристической константой частицы. Значение 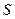 определяют при разных концентрациях и экстраполируют к нулевой концентрации. Для экстраполяции строят зависимость величины, обратной константе седиментации и называемой кинетической седиментационной устойчивостью (КСУ). КСУ обеспечивается гидродинамическими факторами: вязкостью и плотностью среды, плотностью и размером частиц. Необходимость экстраполяции делает метод скоростного ультрацентрифугирования достаточно трудоемким. Этот метод не является абсолютным, так как требует определения коэффициента диффузии независимым методом.
определяют при разных концентрациях и экстраполируют к нулевой концентрации. Для экстраполяции строят зависимость величины, обратной константе седиментации и называемой кинетической седиментационной устойчивостью (КСУ). КСУ обеспечивается гидродинамическими факторами: вязкостью и плотностью среды, плотностью и размером частиц. Необходимость экстраполяции делает метод скоростного ультрацентрифугирования достаточно трудоемким. Этот метод не является абсолютным, так как требует определения коэффициента диффузии независимым методом.
В случае полидисперсных систем с помощью скоростной седиментации можно определить массу разных фракции частиц. Однако, седиментация не всегда позволяет судить о составе дисперсной системы. Так, смесь двух белков - альбумина и гемоглобина - однородна по отношению к скоростной седиментации, так как гидродинамические свойства частиц этих белков одинаковы. Однако, эти белки могут быть разделены методом электрофореза, так как частицы несут на своей поверхности заряд различной величины.
8.4.5. Равновесное ультрацентрифугирование
При равновесном ультрацентрифугировании используют ускорения порядка (103 ¸104) 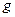 . При установлении равновесия частицы располагаются в виде полосы, ширина которой определяется соотношением процессов седиментации и диффузии. Распределение концентрации вещества в полосе описывается симметричной гауссовой кривой. Количество вещества, переносимого через единицу сечения кюветы, равно
. При установлении равновесия частицы располагаются в виде полосы, ширина которой определяется соотношением процессов седиментации и диффузии. Распределение концентрации вещества в полосе описывается симметричной гауссовой кривой. Количество вещества, переносимого через единицу сечения кюветы, равно 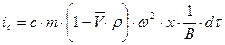 . Обратный поток вещества вследствие диффузии равен
. Обратный поток вещества вследствие диффузии равен 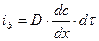 . В условиях равновесия
. В условиях равновесия
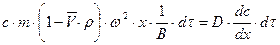 ;
; 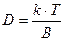 ;
;
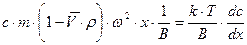 ;
; 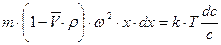 .
.
Интегрируя от 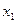 до
до 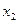 и от
и от 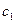 до
до 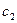 , получим
, получим
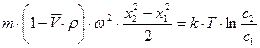 ;
;
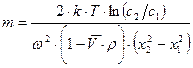 ,
,
где 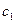 и
и 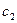 - равновесные концентрации на расстояниях
- равновесные концентрации на расстояниях 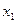 и
и 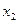 от оси вращения.
от оси вращения.
Равновесное ультрацентрифугирование является абсолютным методом определения масс частиц и макромолекул. Значения масс вычисляются лишь из разности концентраций на расстоянии 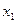 и
и 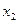 от оси вращения. При работе методом равновесного ультрацентрифугирования необходимо проводить ультрацентрифугирование длительное время.
от оси вращения. При работе методом равновесного ультрацентрифугирования необходимо проводить ультрацентрифугирование длительное время.
Равновесное ультрацентрифугирование связано с термодинамической седиментационной устойчивостью, (ТСУ) измеряемой гипсометрической высотой 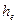 , т.е. высотой, при которой концентрация дисперсной фазы изменяется в
, т.е. высотой, при которой концентрация дисперсной фазы изменяется в 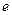 раз. ТСУ не зависит от вязкости и увеличивается с повышением температуры, т.к. усиливается тепловое движение.
раз. ТСУ не зависит от вязкости и увеличивается с повышением температуры, т.к. усиливается тепловое движение.
8.5. Контрольные вопросы
1. Броуновское движение, его причины и общенаучное значение.
2. Как с помощью броуновского движения доказывается статистический характер второго закона термодинамики?
3. Основной постулат теории броуновского движения. Броуновское движение как причина диффузии.
4. Вывод уравнения Эйнштейна - Смолуховского.
5. Что характеризует первый закон Фика? Напишите выражение для этого закона. Что такое коэффициент диффузии, поток диффузии?
6. Что характеризует второй закон Фика? Напишите выражение для этого закона.
7. Напишите выражение для неравновесной концентрации в полубесконечном теле.
8. Дайте определение диффузии.
9. Дайте определение массопроницаемости.
10. Что такое диффузионной и фазовый механизм переноса?
11. Что такое поток Кнудсена и ламинарный поток Пуайзеля?
12. Седиментационное уравнение незаряженной частицы.
13. Ультрацентрифуга. Определение массы частицы методом скоростной седиментации.
14. Можно ли разделить седиментационными методами смесь альбумина и гемоглобина?
15. Определение массы частицы методом седиментационного равновесия.
16. Седиментационный анализ порошков. Построение кривых распределения.
Дата добавления: 2020-11-18; просмотров: 695;











