Смачивание и растекание

Под смачиванием понимают совокупность поверхностных явлений, про­исходящих на границе раздела трех контактирующих фаз, т.е. на линии трехфазного контакта. Оно зависит от взаимодействия молекул внутри каждой из фаз и между фазами и сопровождается убылью свободной энергии. При смачивании рассматриваются систе­мы жидкость - газ - твердое тело или жидкость - жидкость - твердое тело. В последнем случае жидкости должны быть взаимно не смешивающими­ся. Когда конкурируют две жидкости, то смачивание является избирательным. В зависимости от соотношения интенсивности молекулярных сил, действующих между молекулами жидкости и жидкостью и твердым телом, капля жидкости образует с поверхностью твердого тела определенный равновес­ный угол , называемый краевым углом (рис. 5.1), который является характе­ристикой смачивания. Этот угол называется также контактным углом, или углом смачивания. Он образован твердой поверхностью и касатель­ной в точке соприкосновения трех фаз и отсчитывается в сторону более плотной фазы. Установившееся равновесие явля­ется как механическим, так и термодинамическим.

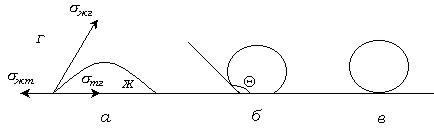
Рис. 5.1. Капля жидкости на поверхности твёрдого тела. ) – смачивание, ) - несмачивание, 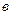) - идеальное несмачивание.

Краевой угол всегда измеряют со стороны жидкости, а при контакте твердо­го тела и двух жидкостей - со стороны более полярной фазы. Если 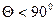, то говорят, что твердое тело смачивается жидкостью. При полном смачи­вании капля растекается на поверхности до образования мономолекуляр­ной пленки и 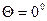. Если 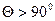, то жидкость не смачивает твердое тело. В случае полного несмачивания капля жидкости имела бы сфериче­скую форму, если бы не действовала сила тяжести и 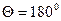. Полное несмачивание реализуется лишь в условиях невесомости. В гравитаци­онном поле Земли максимальное значение угла 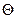достигнуто для капли ртути на поверхности тефлона и равно 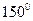. В качестве примеров ниже приведены значения угла смачивания водой различных веществ: кварц - 0°; малахит - 17°; гра­фит - 55°; тальк - 69°; парафин - 106°; тефлон - 108°.

Смачивание зависит от взаимодействия фаз, которое характеризу­ется величиной поверхностного натяжения между фазами. Поверхностная энергия твердого тела стремится уменьшится, что приводит к растека­нию капли по поверхности. Эта энергия равна поверхностному натяжению твердого тела на границе с газом 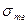. Межфазная энергия на границе твердого тела с жидкостью 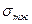стремится сжать каплю, т.к. уменьшение площади поверхности приводит к уменьшению поверхностной энер­гии. Когезионные силы, действующие внутри капли, также препятствуют рас­теканию. Их действие направлено по касательной к поверхности и рав­но 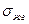. В условиях равновесия, когда капля жидкости перестает рас­текаться, силы поверхностного натяжения уравновешивают друг друга (рис. 5.1 ). Условие равновесия выражается уравнением Юнга:

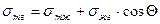
Решив это уравнение относительно 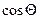, получим:

Поскольку межфазные натяжения на границе с твердым телом не всегда возможно определить экспериментально, то уравнение Юнга чаще используется для решения обратной задачи смачивания, т.е. определения разности межфазных энергий по измеренным величинам краевого угла.

Необходимо отметить, что мениск объемной жидкости образует краевой угол не с сухой подложкой, а с твердой поверхностью, покрытой тонкой смачивающей пленкой.

Подставим в уравнение Дюпре уравнение Юнга:

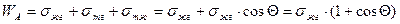
Ранее мы отмечали, что

Поделив правую часть уравнения Дюпре - Юнга на , получим от­ношение работ адгезии и когезии:

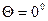
Проанализируем полученное выражение. При 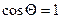, , 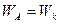что соответствует смачиванию твердого тела жидкостью. При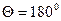 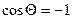, , 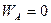что соответствует полному несмачиванию жидкостью твердого тела.

Условие самопроизвольного смачивания, или растекания жидкости, которое выполняется при значени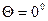и и 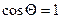, можно записать в виде неравенства: 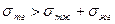или 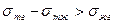. Из уравнения Дюпре следует, что 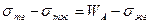. Следовательно 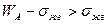или 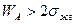, т. е. 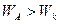. Разность между правой и левой частями неравенств, характеризующих растекание, называется коэффици­ентом растекания по Гаркинсу:

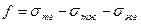
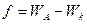
Установление термодинамического и механического равновесия в идеаль­ном случае совпадает. В реальных условиях контактирования жидкостей с твердыми поверхностями термодинамическое равновесие не устанавлива­ется по различным причинам. Среди факторов, влияющих на установление равновесия, следует отметить условия формирования поверхности контакта, порядок соприкосновения жидкости и газа с твердым телом (нанесение капли или подвод воздушного пузырька), а также шероховатость твердой поверхности. Задержка в установлении равновесного значения 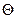называ­ется гистерезисом смачивания. Он выражается также в различии краевых углов натекания и оттекания при перемещении жидкости по поверхности твердого тела. Значение равновесного угла смачивания определяется следующим образом. К капле жидкости, находящейся на поверхности, с помощью микрошприца добавляют жидкость в избытке и измеряют статический угол, являющийся углом натекания (рис. 5.2). Затем отбирают часть жидкости из капли и измеряют статический угол оттекания.

Значение равновесного угла получают как полусумму статических углов натекания и оттекания:

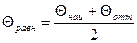
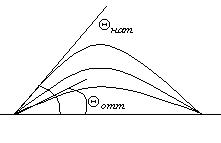
Рис. 5.2. Определение равновесного угла смачивания.

При растекании жидкости с малым поверхностным натяжением по поверхности жидкости с большим поверхностным натяжением проявляется эффект Марангони, т. е. течение жидкости под действием градиента поверхностного натяжения, возникающего из-за локальных неоднородностей состава и температуры в разных участках межфазной поверхности. Жидкость течёт из области малых в область больших поверхностных натяжений вследствие самопроизвольного уменьшения поверхностной энергии Гиббса. При ньютоновском течении напряжение сдвига пропорционально градиенту поверхностного натяжения 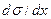, где 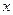- расстояние в направлении движения жидкости, 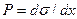. Для раствора ПАВ градиент поверхностного натяжения можно разложить на два множителя:

где первый множитель - поверхностная активность, а второй - градиент концентрации.

Т. к. скорость ньютоновского течения V пропорциональна напряжению сдвига, то

где 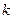- коэффициент пропорциональности, а 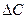- разность концентраций, т. к. градиент концентрации чрезвычайно трудно определить. Следовательно, скорость течения раствора тем выше, чем больше поверхностная активность и чем больше разность концентраций в направлении движения.

Эффект Марангони имеет большое значение в процессах разделения, таких как экстракция, абсорбция и др. Он определяет прочность пенных плёнок. Его можно легко наблюдать на примере разрыва тонкой плёнки воды на ровной поверхности под действием капли спирта. Другой простой опыт состоит в том, что в тарелку с водой помещают спички, собирают их в центре и капают на них мыльную воду. В результате течения поверхностного слоя спички переносятся к краям тарелки.

Поверхностное натяжение на границе твердого тела с газом меньше поверхностного натяжения твердого тела в вакууме 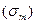из-за адсорбции газа. 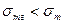. Разность поверхностных натяжений выра­жается через равновесное давление растекания:

где - равновесное давление газа, Г - поверхностная концентрация адсорбированного газа. Запишем уравнение Юнга в виде:

Условие самопроизвольного смачивания может быть записано в виде:

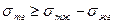или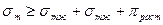

При 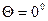жидкость смачивает твердое тело полностью и самопроизвольно растекается по поверхности со скоростью, зависящей от вязкости жидко­сти и от чистоты или рельефа поверхности.

ПАВ увеличивают смачивание, т.к. снижают поверхностное натяжение, и капля лучше растекается на поверхности (рис. 5.3)

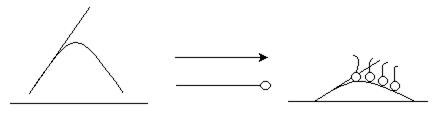
Рис. 5.3. Растекание капли жидкости под действием ПАВ.

По величине краевого угла на границе твердое тело - вода - воз­дух судить о гидрофильности поверхности трудно, т.к. вода хорошо сма­чивает большинство поверхностей. Для разделения поверхностей на гид­рофильные и гидрофобные используют избирательное смачивание водой в присутствии неполярной жидкости, например, гептана. Гидрофильные по­верхности избирательно смачиваются водой, . Для гидрофобных поверхностей углеводород частично вытесняет воду и .