ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМАХ
ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ
СТЕРЖНЕВОЙ СИСТЕМЫ
Любая конструкция при действии внешних сил деформируется. Для проверки жесткости конструкции необходимо определять перемещения, обусловленные деформациями ее элементов.
В основе классических методов строительной механики лежит понятие линейно-деформируемой упругой системы (конструкции). Перемещения в такой системе линейно зависят от внешних обобщенных сил 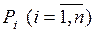 :
:
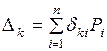 . (1.2.1)
. (1.2.1)
Здесь 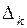 - перемещение точки “k” системы по определенному направлению от внешних сил
- перемещение точки “k” системы по определенному направлению от внешних сил 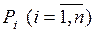 ;
; 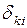 - то же от силы
- то же от силы 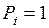 .
.
В процессе деформирования упругой системы внешние и внутренние силы системы совершают работу. При статическом действии внешних сил их работа вычисляется по формуле
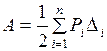 . (1.2.2)
. (1.2.2)
Далее будут рассматриваться только плоские стержневые системы, нагруженные в их плоскости. В стержнях таких систем в общем случае действуют, как известно, три внутренние силы: продольная сила 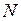 ; поперечная сила
; поперечная сила 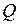 и изгибающий момент
и изгибающий момент 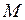 . Их работа определяется по формуле
. Их работа определяется по формуле
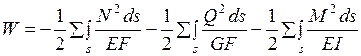 . (1.2.3)
. (1.2.3)
Здесь 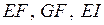 - жесткости стержней соответственно при растяжении-сжатии, сдвиге и изгибе;
- жесткости стержней соответственно при растяжении-сжатии, сдвиге и изгибе; 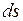 - дифференциал локальной координаты
- дифференциал локальной координаты 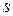 на каждом участке конструкции; суммы берутся по всем участкам конструкции.
на каждом участке конструкции; суммы берутся по всем участкам конструкции.
Потенциальная энергия деформации 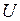 любой упругой системы равна работе
любой упругой системы равна работе 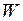 внутренних сил, взятой с обратным знаком:
внутренних сил, взятой с обратным знаком: 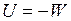 . Для плоской стержневой системы из формулы (1.2.3) следует:
. Для плоской стержневой системы из формулы (1.2.3) следует:
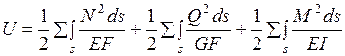 . (1.2.4)
. (1.2.4)
Выражение для 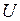 нелинейно зависит от внутренних сил
нелинейно зависит от внутренних сил 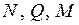 . Поэтому к нему нельзя применить принцип независимости действия сил, т. е. потенциальная энергия деформации
. Поэтому к нему нельзя применить принцип независимости действия сил, т. е. потенциальная энергия деформации 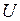 от внешних сил
от внешних сил 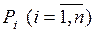 не равна сумме
не равна сумме 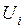 от каждой силы в отдельности.
от каждой силы в отдельности.
Практика расчетов стержневых систем показала, что в таких конструкциях, как балки, рамы и арки, перемещения в основном обусловлены изгибом стержней. Для таких конструкций в формуле (1.2.4) можно учитывать только последнее слагаемое:
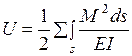 . (1.2.5)
. (1.2.5)
Для ферм следует брать слагаемое, содержащее продольные силы 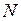 (
( 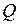 и
и 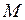 в стержнях ферм согласно общепринятой расчетной схеме считаются равными нулю):
в стержнях ферм согласно общепринятой расчетной схеме считаются равными нулю):
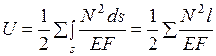 . (1.2.6)
. (1.2.6)
Здесь 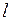 - длина стержня. Сумма берется по всем стержням фермы. Второе слагаемое формулы (1.2.4) (вместе с третьим слагаемым) следует учитывать только при весьма коротких стержнях конструкции:
- длина стержня. Сумма берется по всем стержням фермы. Второе слагаемое формулы (1.2.4) (вместе с третьим слагаемым) следует учитывать только при весьма коротких стержнях конструкции: 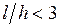 ;
; 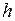 - высота поперечного сечения стержня.
- высота поперечного сечения стержня.
ТЕОРЕМА КАСТИЛИАНО
Формулировка теоремы. Частная производная от потенциальной энергии деформации 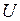 упругой системы по некоторой внешней обобщенной силе
упругой системы по некоторой внешней обобщенной силе 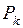 равна обобщенному перемещению
равна обобщенному перемещению 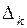 в направлении этой силы:
в направлении этой силы:
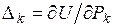 . (1.2.7)
. (1.2.7)
Доказательство теоремы. Пусть 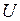 - потенциальная энергия деформации системы от внешних обобщенных сил
- потенциальная энергия деформации системы от внешних обобщенных сил 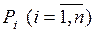 , представленная как функция этих сил:
, представленная как функция этих сил: 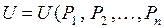 ). Зададим некоторой силе
). Зададим некоторой силе 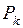 бесконечно малое приращение
бесконечно малое приращение  и найдем потенциальную энергию деформации системы с учетом этого приращения:
и найдем потенциальную энергию деформации системы с учетом этого приращения:
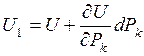 . (1.2.8)
. (1.2.8)
Изменим порядок приложения сил. Сначала к системе приложим только силу  и найдем потенциальную энергию деформации от этой силы:
и найдем потенциальную энергию деформации от этой силы:
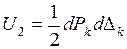 . (1.2.9)
. (1.2.9)
Здесь  - бесконечно малое перемещение от силы
- бесконечно малое перемещение от силы  в направлении этой силы. Затем приложим к системе все остальные силы
в направлении этой силы. Затем приложим к системе все остальные силы 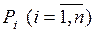 . Потенциальная энергия деформации системы после этого будет такой:
. Потенциальная энергия деформации системы после этого будет такой:
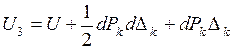 . (1.2.10)
. (1.2.10)
Последнее слагаемое в (1.2.10) представляет работу силы  на перемещении
на перемещении 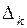 от сил
от сил 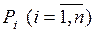 . Так как
. Так как 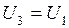 , то
, то
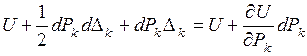 . (1.2.11)
. (1.2.11)
Из выражения (1.2.11) после отбрасывания слагаемого 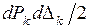 , имеющего второй прядок малости, следует:
, имеющего второй прядок малости, следует:
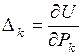 , (1.2.12)
, (1.2.12)
что и требовалось доказать.
Теорема Кастилиано позволяет определить перемещение 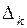 в направлении любой имеющейся силы
в направлении любой имеющейся силы 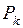 . Если же в направлении искомого перемещения
. Если же в направлении искомого перемещения 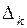 силы
силы 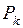 нет, то необходимо в направлении
нет, то необходимо в направлении 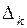 добавить некоторую фиктивную силу
добавить некоторую фиктивную силу 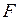 и определить
и определить 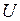 с учетом этой силы. Далее по теореме Кастилиано определяется
с учетом этой силы. Далее по теореме Кастилиано определяется 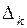 , после чего полагается
, после чего полагается  :
:
 . (1.2.13)
. (1.2.13)
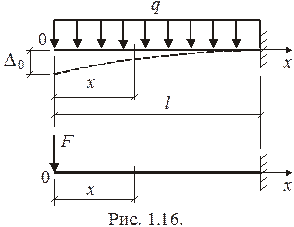
Найдем прогиб 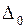 свободного конца консольной балки от распределенной нагрузки
свободного конца консольной балки от распределенной нагрузки 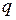 (рис. 1.16) при постоянной жесткости
(рис. 1.16) при постоянной жесткости 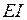 . Так как в направлении
. Так как в направлении 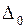 сосредоточенной силы нет, то прикладываем в этом направлении фиктивную силу
сосредоточенной силы нет, то прикладываем в этом направлении фиктивную силу 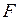 и находим потенциальную энергию деформации балки с учетом этой силы:
и находим потенциальную энергию деформации балки с учетом этой силы:
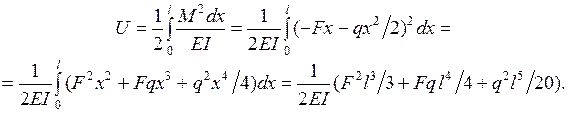
По теореме Кастилиано получаем
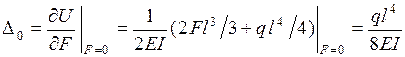 .
.
ФОРМУЛА МОРА
 С помощью теоремы Кастилиано можно получить удобную в практическом использовании формулу для вычисления перемещений в стержневых системах, называемую формулой Мора. Ранее отмечалось, что в таких конструкциях, как балки, рамы и арки, перемещения в основном обусловлены изгибом стержней. В этом случае потенциальную энергию деформации
С помощью теоремы Кастилиано можно получить удобную в практическом использовании формулу для вычисления перемещений в стержневых системах, называемую формулой Мора. Ранее отмечалось, что в таких конструкциях, как балки, рамы и арки, перемещения в основном обусловлены изгибом стержней. В этом случае потенциальную энергию деформации 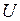 можно определять только с учетом изгибающих моментов
можно определять только с учетом изгибающих моментов 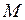 :
:
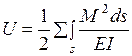 . (1.2.14)
. (1.2.14)
Требуется определить перемещение некоторой точки “k” конструкции по направлению 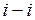 от заданной нагрузки (рис. 1.17). Для этого в направлении искомого перемещения
от заданной нагрузки (рис. 1.17). Для этого в направлении искомого перемещения  добавим фиктивную силу
добавим фиктивную силу 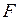 и определим потенциальную энергию деформации конструкции с учетом данной силы:
и определим потенциальную энергию деформации конструкции с учетом данной силы:
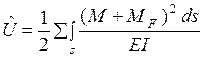 . (1.2.15)
. (1.2.15)
Здесь 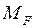 - изгибающие моменты в стержнях конструкции от силы
- изгибающие моменты в стержнях конструкции от силы 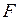 . В упругой конструкции моменты
. В упругой конструкции моменты 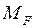 линейно зависят от силы
линейно зависят от силы 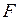 :
: 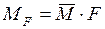 , где
, где 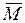 - изгибающие моменты от силы
- изгибающие моменты от силы 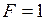 . Выражение (1.2.15) после этого примет вид
. Выражение (1.2.15) после этого примет вид
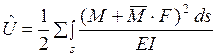 . (1.2.16)
. (1.2.16)
По теореме Кастилиано
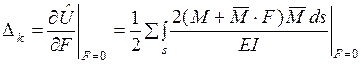 . (1.2.17)
. (1.2.17)
Это дает формулу Мора
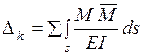 . (1.2.18)
. (1.2.18)
Для нахождения перемещения 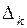 по данной формуле необходимо:
по данной формуле необходимо:
а) определить функции 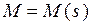 на каждом участке конструкции от заданной нагрузки;
на каждом участке конструкции от заданной нагрузки;
б) определить функции 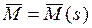 на каждом участке конструкции от силы
на каждом участке конструкции от силы 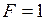 в направлении искомого перемещения
в направлении искомого перемещения 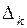 ;
;
в) вычислить интегралы Мора  по участкам конструкции;
по участкам конструкции;
г) просуммировать полученные интегралы.
Примечание. По формуле Мора можно определять как линейные перемещения, так и углы поворота поперечных сечений стержней конструкции. В последнем случае изгибающие моменты 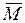 находятся от момента
находятся от момента 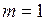 , приложенного в сечении, где определяется угол поворота.
, приложенного в сечении, где определяется угол поворота.
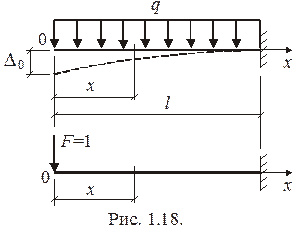 Применим формулу Мора для определения прогиба
Применим формулу Мора для определения прогиба 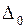 прежней балки (рис. 1.18). Изгибающие моменты
прежней балки (рис. 1.18). Изгибающие моменты 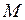 и
и 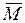 необходимо представить как функции координаты
необходимо представить как функции координаты 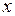 произвольного сечения балки:
произвольного сечения балки: 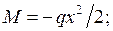
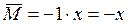 . Определяем прогиб
. Определяем прогиб 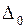 :
:
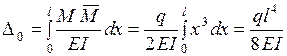 .
.
Полученный результат совпадает с тем, что был найден по теореме Кастилиано.
ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ МОРА
ПО ПРАВИЛУ ВЕРЕЩАГИНА
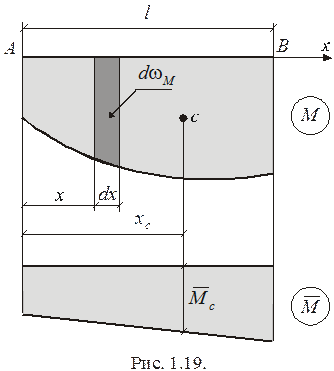
Правило Верещагина применяется для вычисления интегралов Мора на прямолинейных участках конструкции, имеющих постоянную жесткость 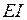 . Рассмотрим прямолинейный участок AB (рис. 1.19). Изгибающий момент
. Рассмотрим прямолинейный участок AB (рис. 1.19). Изгибающий момент 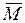 на таком участке является линейной функцией локальной координаты
на таком участке является линейной функцией локальной координаты 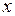 :
: 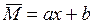 , где
, где 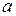 и
и 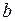 - некоторые постоянные. Вычислим интеграл Мора:
- некоторые постоянные. Вычислим интеграл Мора:
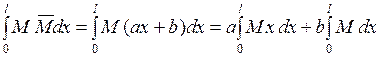
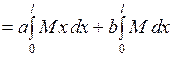 . (1.2.19)
. (1.2.19)
Определенные интегралы в правой части данного выражения имеют известный геометрический смысл: 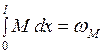 - площадь эпюры
- площадь эпюры 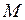 на участке AB;
на участке AB;  - статический момент площади
- статический момент площади 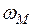 относительно начала участка AB (
относительно начала участка AB ( 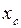 - абсцисса центра тяжести эпюры
- абсцисса центра тяжести эпюры 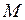 ). С учетом этого получаем
). С учетом этого получаем
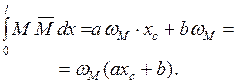
Так как 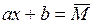 , то
, то 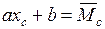 - ордината эпюры
- ордината эпюры 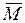 под центром тяжести эпюры
под центром тяжести эпюры 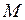 . Таким образом, получаем правило Верещагина для вычисления интегралов Мора:
. Таким образом, получаем правило Верещагина для вычисления интегралов Мора:
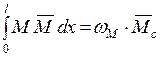 . (1.2.20)
. (1.2.20)
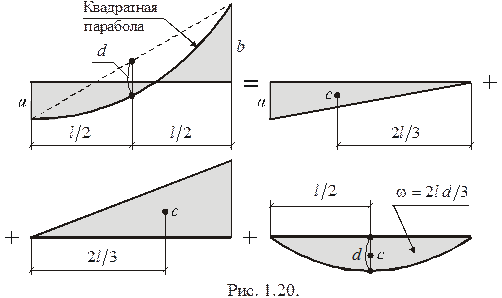
Из выражения (1.2.20) видно, что для вычисления интеграла Мора по правилу Верещагина необходимо иметь площадь эпюры  и положение ее центра тяжести. Эти данные легко определяются только для некоторых простых эпюр. Если эпюра
и положение ее центра тяжести. Эти данные легко определяются только для некоторых простых эпюр. Если эпюра  является сложной, то ее можно разбить на несколько простых эпюр так (рис. 1.20), чтобы площадь и положение центра тяжести каждой из них легко определялись. Тогда правило Верещагина можно применить к каждой простой эпюре, и затем просуммировать полученные результаты.
является сложной, то ее можно разбить на несколько простых эпюр так (рис. 1.20), чтобы площадь и положение центра тяжести каждой из них легко определялись. Тогда правило Верещагина можно применить к каждой простой эпюре, и затем просуммировать полученные результаты.
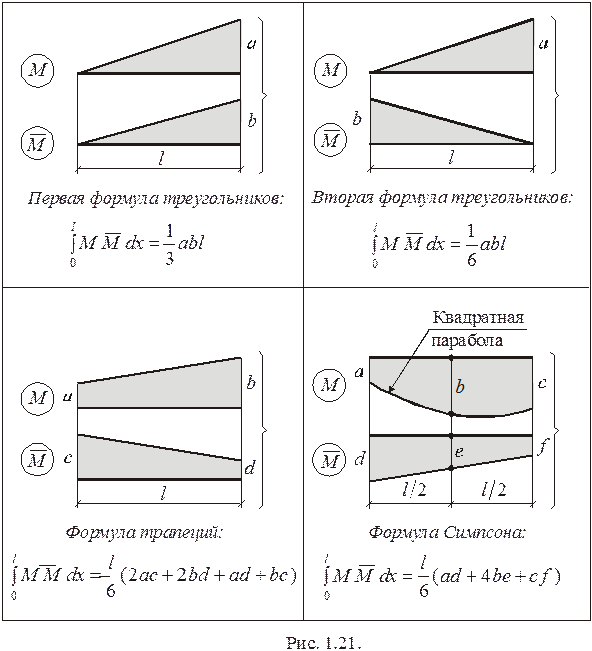
СПРАВОЧНЫЕ ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ
ИНТЕГРАЛОВ МОРА
С помощью правила Верещагина или путем непосредственного интегрирования можно получить формулы для вычисления интегралов Мора от произведения часто встречающихся эпюр  и
и  . Ниже приведены четыре основные справочные формулы (рис. 1.21).
. Ниже приведены четыре основные справочные формулы (рис. 1.21).
Пример. Определить прогиб  статически определимой балки (рис. 1.22а). Исходные данные:
статически определимой балки (рис. 1.22а). Исходные данные: 
Решение.
Определяем реакции опор:
Находим изгибающие моменты на участках балки.
Участок AB: 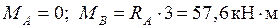 .
.
Участок BC: 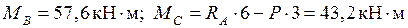 .
.
Участок ED: 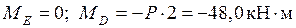 .
.
Участок DC: 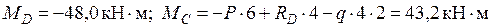 .
.
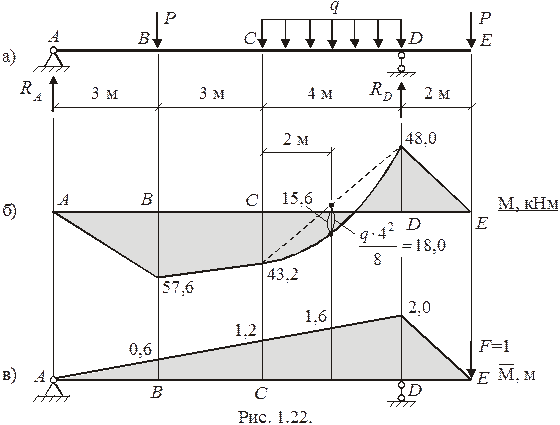
По полученным результатам строим эпюру  (рис. 1.22б). Для определения
(рис. 1.22б). Для определения  прикладываем в точке E силу
прикладываем в точке E силу  и строим от нее эпюру
и строим от нее эпюру  (рис. 1.22в) при движении с правого конца балки (в этом случае реакции опор от силы
(рис. 1.22в) при движении с правого конца балки (в этом случае реакции опор от силы 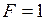 можно не определять). Определяем
можно не определять). Определяем  , вычисляя интегралы Мора на участках балки по приведенным выше справочным формулам:
, вычисляя интегралы Мора на участках балки по приведенным выше справочным формулам:
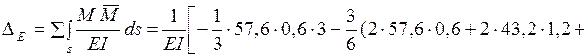
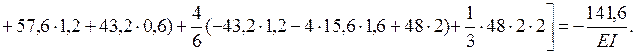
Знак “-“ в результате означает, что точка E балки перемещается противоположно силе 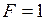 , т.е. вверх.
, т.е. вверх.
Дата добавления: 2016-07-27; просмотров: 2921;











