Искривление пространства и формирование Черных дыр
Закон всемирного тяготения, открытый И. Ньютоном (1687 г.), стимулировал развитие астрономических идей. Вначале Митчелл (1783 г.), затем Лаплас (1796 г.) предсказали возможность существования звезд с таким сильным гравитационным полем, которое задерживает световые фотоны, и поэтому такие звезды становятся невидимыми. Впоследствии их назвали Черными дырами.
В 1916 г. немецкий астроном и физик Карл Шварцшильд предложил формулу для расчета гравитационного радиуса 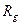 Черной дыры, которая следует из законов Классической механики. С тех пор эта формула и используется в астрономических расчетах, а гравитационный радиус называется Шварцшильдовским радиусом.
Черной дыры, которая следует из законов Классической механики. С тех пор эта формула и используется в астрономических расчетах, а гравитационный радиус называется Шварцшильдовским радиусом.
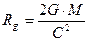 , (342)
, (342)
где 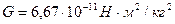 - гравитационная постоянная;
- гравитационная постоянная; 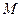 - масса звезды;
- масса звезды; 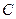 - скорость света.
- скорость света.
Известно, что по мере уменьшения длины волны фотона (от инфракрасного до гамма диапазона) его энергия 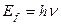 увеличивается примерно на 15 порядков (табл. 4). В такой же последовательности растет и возможность фотона преодолевать силу гравитации, но формула (332) не учитывает этот факт. Поэтому у нас есть основания полагать, что при её выводе была допущена ошибка. В чем её суть?
увеличивается примерно на 15 порядков (табл. 4). В такой же последовательности растет и возможность фотона преодолевать силу гравитации, но формула (332) не учитывает этот факт. Поэтому у нас есть основания полагать, что при её выводе была допущена ошибка. В чем её суть?
Формула (332) была получена следующим образом. За основу было взято математическое соотношение закона всемирного тяготения
 , (343)
, (343)
здесь: 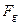 - сила гравитации;
- сила гравитации; 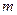 - масса фотона;
- масса фотона;  - расстояние между центрами масс тел, формирующих гравитацию.
- расстояние между центрами масс тел, формирующих гравитацию.
Чтобы найти гравитационный радиус 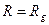 звезды, при котором её гравитационное поле задерживает свет, надо найти равенство между силой гравитации
звезды, при котором её гравитационное поле задерживает свет, надо найти равенство между силой гравитации 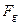 и силой
и силой 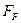 , движущей фотон. Однако, сделать это при полном отсутствии информации об электромагнитной (магнитной) структуре фотона не так просто. Поэтому за основу была взята идея равенства между энергией фотона
, движущей фотон. Однако, сделать это при полном отсутствии информации об электромагнитной (магнитной) структуре фотона не так просто. Поэтому за основу была взята идея равенства между энергией фотона  и потенциальной энергией гравитационного поля
и потенциальной энергией гравитационного поля 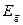 . Если предположить, что сила гравитации
. Если предположить, что сила гравитации 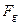 совершает работу на расстоянии, равном гравитационному радиусу
совершает работу на расстоянии, равном гравитационному радиусу 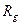 , то эта работа будет равна
, то эта работа будет равна
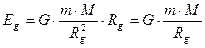 . (344)
. (344)
Связь между энергией фотона 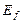 , длиной его волны
, длиной его волны 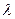 , частотой колебаний
, частотой колебаний 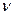 и скоростью
и скоростью 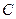 определяется зависимостями:
определяется зависимостями:
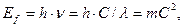 (345)
(345)
где: 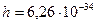 Дж с - постоянная Планка;
Дж с - постоянная Планка; 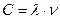 .
.
Далее предполагалось, что фотон будет двигаться в гравитационном поле звезды со скоростью 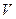 и поэтому его кинетическая энергия должна определяться соотношением
и поэтому его кинетическая энергия должна определяться соотношением 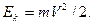 При
При 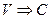 имеем
имеем
 (346)
(346)
Из описанного следует, что гравитационное поле звезды будет задерживать фотон при равенстве между её потенциальной энергией (344) и кинетической энергией фотона (346), то есть
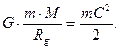 (347)
(347)
Отсюда получаем формулу для расчета гравитационного радиуса, предложенную К. Шварцшильдом
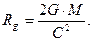 (348)
(348)
Мы уже показали, что скорость центра масс фотона изменяется в интервале длины его волны таким образом, что её средняя величина остаётся постоянной и равной скорости света (рис. 12). Это дает нам основание определить в первом приближении силу 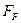 , движущую фотон, путем деления его энергии на длину волны.
, движущую фотон, путем деления его энергии на длину волны.
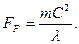 (349)
(349)
Приравнивая силу гравитации (343) 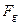 и силу, движущую фотон (349)
и силу, движущую фотон (349) 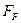 , имеем
, имеем
 (350)
(350)
Отсюда имеем
 . (351)
. (351)
Из изложенного следует, что для определения гравитационного радиуса Черной дыры необходимо использовать равенство между гравитационной силой и силой, движущей фотон, но не равенство энергий. Силу (349), движущую фотон, можно записать так
 , (352)
, (352)
где 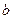 - коэффициент, величина которого зависит от используемого при расчете ускорения центра масс фотона.
- коэффициент, величина которого зависит от используемого при расчете ускорения центра масс фотона.
Для максимального полного ускорения фотона 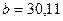 , для максимального касательного ускорения
, для максимального касательного ускорения 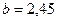 , а для максимального значения проекции полного ускорения на ось
, а для максимального значения проекции полного ускорения на ось 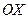 , совпадающей с направлением движения центра масс фотона,
, совпадающей с направлением движения центра масс фотона, 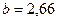 . В прежних наших публикациях мы приняли
. В прежних наших публикациях мы приняли 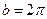 , что соответствует максимальному полному ускорению точки условной окружности радиуса
, что соответствует максимальному полному ускорению точки условной окружности радиуса  (рис. 9). Так как величина указанного коэффициента незначительно влияет на величину ускорения центра масс фотона, то для рассматриваемого нами случая примем
(рис. 9). Так как величина указанного коэффициента незначительно влияет на величину ускорения центра масс фотона, то для рассматриваемого нами случая примем 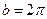 .
.
При равенстве между силой (352) 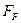 , движущей фотон, и силой гравитации (343)
, движущей фотон, и силой гравитации (343) 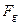 гравитационного поля и учете соотношения (351), гравитационный радиус
гравитационного поля и учете соотношения (351), гравитационный радиус 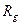 определится по формуле
определится по формуле
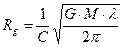 . (353)
. (353)
Тогда сила 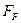 , движущая световой фотон с длиной волны
, движущая световой фотон с длиной волны  м со скоростью
м со скоростью  м/c, будет равна
м/c, будет равна
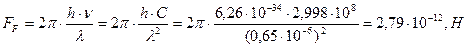 (354)
(354)
Учитывая, что масса Солнца  кг, радиус Солнца
кг, радиус Солнца  м,
м, 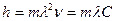 , постоянная гравитации
, постоянная гравитации 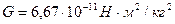 и обозначая массу фотона через
и обозначая массу фотона через 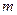 , определим силу
, определим силу 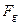 гравитации Солнца, действующую на пролетающий мимо фотон, по формуле
гравитации Солнца, действующую на пролетающий мимо фотон, по формуле
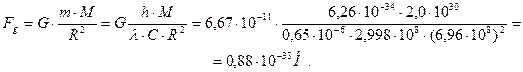 (355)
(355)
Тангенс угла отклонения фотона от прямолинейного движения при его пролете вблизи Солнца будет равен 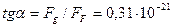 (рис. 186).
(рис. 186).
Известно, неудержимое стремление Артура Эддингтона – руководителя астрофизической экспедиции по наблюдению солнечного затмения (1919г) доказать достоверность эйнштейновской теории об искривлении пространства. Если бы Эддингтон владел, излагаемой нами элементарной информацией, то он, конечно, не поехал бы в Африку, где затмение Солнца было максимально. Ему достаточно было бы рассчитать ожидаемый результат измерений по формуле (356) и убедиться в отсутствии возможности доказать достоверность эйнштейновской теории и понять её ошибочность. Сделаем это за него
Если фотон с длиной волны  пролетает вблизи Солнца по прямой, которая параллельна линии, соединяющей центры масс Солнца и Земли, то величина его отклонения
пролетает вблизи Солнца по прямой, которая параллельна линии, соединяющей центры масс Солнца и Земли, то величина его отклонения  от прямолинейного движения в окрестностях Земли будет равна
от прямолинейного движения в окрестностях Земли будет равна
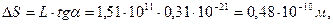 (356)
(356)
где 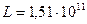 м - расстояние от Земли до Солнца.
м - расстояние от Земли до Солнца.
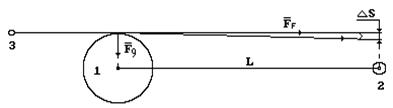
Рис. 186. Схема к анализу искривления траектории фотона гравитационным полем Солнца:
1-Солнце; 2- Земля; 3- звезда
Наука пока не располагает приборами, способными зафиксировать величину 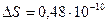 м (рис. 186). Даже если бы удалось измерить её, то она доказала бы искривление траектории фотона, летящего от звезды, гравитационным полем Солнца, но не искривление пространства.
м (рис. 186). Даже если бы удалось измерить её, то она доказала бы искривление траектории фотона, летящего от звезды, гравитационным полем Солнца, но не искривление пространства.
Гравитационный радиус 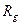 Солнца, при котором оно превращается в Черную дыру, сейчас определяется по формуле (348), не учитывающей длину волны фотона
Солнца, при котором оно превращается в Черную дыру, сейчас определяется по формуле (348), не учитывающей длину волны фотона
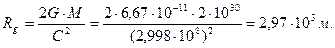 (357)
(357)
Определим гравитационные радиусы Солнца для инфракрасного, светового и гамма фотонов со следующими длинами волн соответственно: 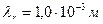 ,
, 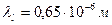 и
и 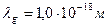 по формуле (353).
по формуле (353).
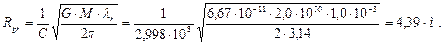 (358)
(358)
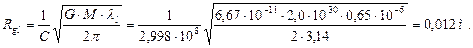 (359)
(359)
 (360)
(360)
В обычном состоянии плотность  вещества Солнца равна 1,4 кг/
вещества Солнца равна 1,4 кг/  . После сжатияплотность вещества Солнца будет зависеть от гравитационного радиуса, определяемого по формулам (357), (358), (359) и (360) соответственно
. После сжатияплотность вещества Солнца будет зависеть от гравитационного радиуса, определяемого по формулам (357), (358), (359) и (360) соответственно
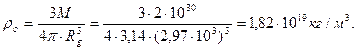
(361)
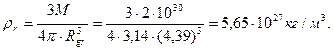 (362)
(362)
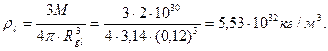 (363)
(363)
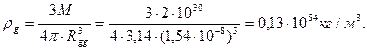 (364)
(364)
Напомним, что плотность ядер атомов оценивается величиной 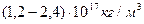 .
.
Теперь видно, что если Солнце сожмется до гравитационного радиуса 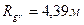 (358), то его поле гравитации будет задерживать только излучение далекой инфракрасной области спектра. Фотоны с меньшей длиной волны оно будет пропускать свободно. Чтобы задерживались фотоны всех частот, гравитационный радиус Солнца должен быть равен
(358), то его поле гравитации будет задерживать только излучение далекой инфракрасной области спектра. Фотоны с меньшей длиной волны оно будет пропускать свободно. Чтобы задерживались фотоны всех частот, гравитационный радиус Солнца должен быть равен 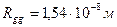 (360), что вряд ли возможно, так как в этом случае плотность вещества Солнца (364) должна быть на 37 порядков больше плотности ядер атомов.
(360), что вряд ли возможно, так как в этом случае плотность вещества Солнца (364) должна быть на 37 порядков больше плотности ядер атомов.
Таким образом, ошибка в определении гравитационного радиуса Солнца, как Черной дыры по формуле (360), не учитывающей длину волны электромагнитного излучения, составляет одиннадцать порядков, но астрономы до сих пор не знают этого.
Если в Природе есть объекты с такой сильной гравитацией, которая задерживает фотоны всех частот, то они не могут быть все черными. Их цвета должны меняться в полном соответствии с изменением цветов фотонов, которые эти объекты не могут задержать. Первыми будут задерживаться фотоны инфракрасной области спектра, затем, по мере уменьшения гравитационного радиуса, фотоны светового, ультрафиолетового, рентгеновского и гамма диапазонов. Дыра становится черной только при гравитационном радиусе, соответствующем гамма фотону с минимальной длиной волны.
Астрофизики зафиксировали, что орбитальный период объекта Лебедь Х-1 совпадает с периодом рентгеновского затмения от этого объекта. Это интересный результат, но он имеет и другие варианты интерпретации. Например, излучение рентгеновских фотонов лишь одной стороной этого объекта. В этом случае указанные периоды тоже будут совпадать.
Дата добавления: 2020-11-18; просмотров: 422;











