Представим формализованное решение предлагаемой задачи.

Модель будет содержать следующие параметры:

Хi — привлекательность дестинации по оценке i-го эксперта, i = 1, 2, …, I, где I — количество экспертов;

Yj — выбранные показатели, j = 1, 2, …, J, где J — количество показателей;

Yjp — признаки показателей, j = 1, 2, …, J — соответствует номеру показателя, p = 1, 2, …, d(m) — количество признаков у данного показателя;

Yjpq — уровни оценок признаков, q = 1, 2, …, Q, где Q — количество уровней оценок;

Rj, rp — весовые коэффициенты.

Модель позволяет найти F(Xi) — неотрицательное число, которое будет тем больше, чем более привлекательна дестинация.

Составляющими Хi являются выбранные показатели Yj, которые и определяют привлекательность дестинации. В качестве показателей могут выступать наличие туристских ресурсов, инфраструктуры, доступность дестинации, лояльное отношение к туристам местного населения и пр. Каждому из показателей приписывается весовой коэффициент Rj, который определяется экспертным путем. Для более точного определения индивидуальных характеристик показателя и объективной его оценки каждый из составляющих показателей подразделяется на несколько признаков Yjp, для которых также устанавливаются весовые коэффициенты rp и разрабатывается шкала оценки (уровни).

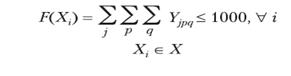В результате решения по данной модели определяется сумма баллов конкретной дестинации, которая соответствует сумме баллов, определенных уровнем оценок признаков, взятых из оценочной шкалы. Причем эта величина будет стремиться (ограничена сверху) к общей сумме баллов, которые может набрать «идеальная» дестинация. Для удобства расчетов эта величина определяется в 1000 баллов:

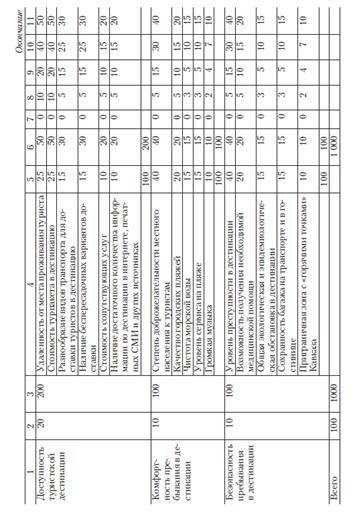
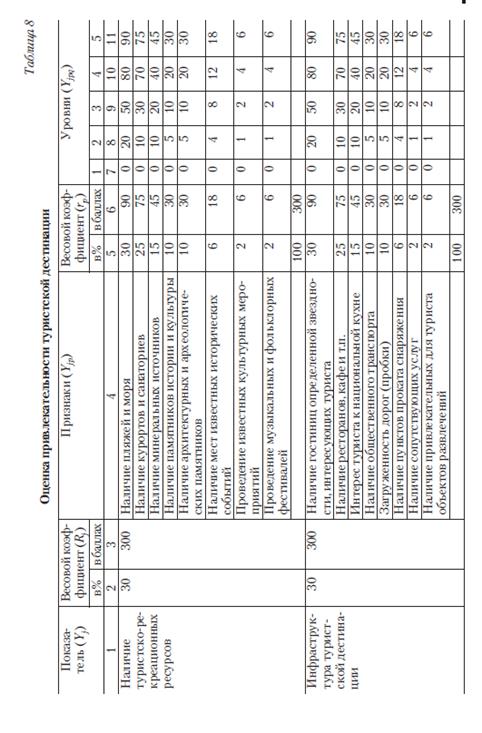Для оценки привлекательности туристской дестинации модель представлена в виде таблицы 8, в которой отображаются те показатели, по которым требуется оценить дестинацию с точки зрения ее привлекательности.

3.