Волновая теория фотона
Тут уместно обратить внимание на интересную особенность шестигранной механической модели (рис. 6, b). Если взять несколько шестигранников разных размеров и разместить их на наклонной плоскости, то все они будут скатываться вниз с одной и той же постоянной скоростью 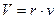 , но с разной частотой (табл. 5).
, но с разной частотой (табл. 5).
Таблица 5. Кинематические параметры движения тел
| Форма тел | 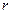 , м , м
| t, с | V, м/с | 
|
| Цилиндрические | 0,008 0,010 0,0!3 | 2,43 2,30 2,05 | 0,83 0,89 0,99 | - - - |
| Шестигранные | 0,0065 0,0080 0,0130 | 5,68 5,67 5,67 | 0,18 0,18 0,18 | 27,69 22,50 13,85 |
Обратим внимание на то, что при увеличении радиуса 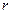 шестигранника частота
шестигранника частота 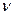 его движения уменьшается так же, как и у фотона. Конечно, у фотона нет плоскости, по которой он мог бы перемещаться, как тела, представленные в табл. 5. Однако, мы уже показали, что центр масс электромагнитной (магнитной) модели фотона описывает укороченную циклоиду, осью симметрии которой является прямолинейная ось ОХ, лежащая в плоскости его поляризации.
его движения уменьшается так же, как и у фотона. Конечно, у фотона нет плоскости, по которой он мог бы перемещаться, как тела, представленные в табл. 5. Однако, мы уже показали, что центр масс электромагнитной (магнитной) модели фотона описывает укороченную циклоиду, осью симметрии которой является прямолинейная ось ОХ, лежащая в плоскости его поляризации.
Начнем с вывода уравнений движения центра масс 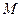 фотона. Поскольку центр масс фотона движется в плоскости поляризации и в рамках аксиомы Единства пространства – материи – времени, то для описания его движения по волновой траектории необходимо иметь два параметрических уравнения.
фотона. Поскольку центр масс фотона движется в плоскости поляризации и в рамках аксиомы Единства пространства – материи – времени, то для описания его движения по волновой траектории необходимо иметь два параметрических уравнения.
Так как центр масс 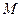 фотона движется относительно наблюдателя и относительно геометрического центра
фотона движется относительно наблюдателя и относительно геометрического центра 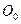 , который движется прямолинейно со скоростью
, который движется прямолинейно со скоростью 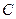 , то для полного описания такого движения необходимо иметь две системы отсчета (рис. 4 и 10): неподвижную
, то для полного описания такого движения необходимо иметь две системы отсчета (рис. 4 и 10): неподвижную 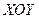 и подвижную
и подвижную  .
.
Амплитуда 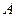 колебаний центра масс
колебаний центра масс 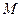 фотона будет равна радиусу
фотона будет равна радиусу 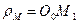 его вращения относительно геометрического центра
его вращения относительно геометрического центра 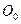 фотона. Из рис. 9 имеем
фотона. Из рис. 9 имеем
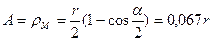 . (37)
. (37)
Обратим внимание на небольшую величину амплитуды 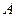 колебаний центра масс фотона в долях длины его волны или радиуса вращения
колебаний центра масс фотона в долях длины его волны или радиуса вращения 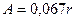 .
.
Уравнения движения центра масс 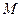 фотона относительно подвижной системы
фотона относительно подвижной системы  имеют вид параметрических уравнений окружности (рис. 4 и 9):
имеют вид параметрических уравнений окружности (рис. 4 и 9):
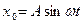 ; (38)
; (38)
 . (39)
. (39)
Если фотон движется относительно неподвижной системы отсчета ХОУ со скоростью  , то уравнения такого движения становятся уравнениями циклоиды:
, то уравнения такого движения становятся уравнениями циклоиды:
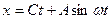 ; (40)
; (40)
 . (41)
. (41)
Обратим внимание на то, что в уравнениях (40) и (41)  и
и 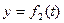 . Это значит, что они описывают движение центра масс фотона по волновой траектории в рамках аксиомы Единства пространства – материи – времени. Отметим, что уравнения Луи Де Бройля и Шредингера этим свойством не обладают. Учитывая соотношения (20), (21) и (37), получим:
. Это значит, что они описывают движение центра масс фотона по волновой траектории в рамках аксиомы Единства пространства – материи – времени. Отметим, что уравнения Луи Де Бройля и Шредингера этим свойством не обладают. Учитывая соотношения (20), (21) и (37), получим:
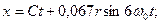 (42)
(42)
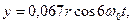 (43)
(43)
где  .
.
На рис. 10 представлены траектории точек  , показанные на (рис. 4). Обратим внимание на важные особенности. Радиус кольца равен
, показанные на (рис. 4). Обратим внимание на важные особенности. Радиус кольца равен 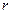 и точка
и точка 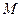 , лежащая на кольце (рис. 4), описывает обыкновенную циклоиду М (рис. 10).
, лежащая на кольце (рис. 4), описывает обыкновенную циклоиду М (рис. 10).
Радиус окружности, описываемой точкой 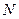 (рис. 4 и 10), -
(рис. 4 и 10), - 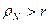 и эта точка описывает удлинённую циклоиду
и эта точка описывает удлинённую циклоиду 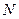 (рис. 10).
(рис. 10).
Радиус окружности, описываемой точкой 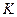 (рис. 4 и 10),
(рис. 4 и 10),  , и она описывает укороченную циклоиду
, и она описывает укороченную циклоиду 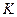 (рис. 10).
(рис. 10).

Рис. 10. Траектории движения точек  , представленных на рис. 4:
, представленных на рис. 4:
М – обыкновенная циклоида; N – удлинённая циклоида; К – укороченная циклоида
Так как у модели фотона амплитуда 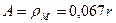 , то его центр масс движется по укороченной циклоиде (42), (43).
, то его центр масс движется по укороченной циклоиде (42), (43).
Результаты табл. 5 требуют, чтобы математическая модель, описывающая скорость центра масс шестигранника, а значит и фотона, не зависела бы от его радиуса 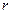 вращения. Уравнения (42) и (43) автоматически дают такой результат
вращения. Уравнения (42) и (43) автоматически дают такой результат
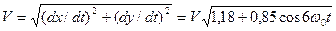 . (44)
. (44)
Если считать, что движение фотона эквивалентно движению шестигранника, то  и получаем закономерность изменения скорости центра масс фотона
и получаем закономерность изменения скорости центра масс фотона
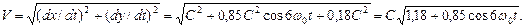 (45)
(45)
График изменения скорости (45) центра масс фотона показан на рис. 11. Как видно, скорость центра масс 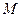 фотона действительно изменяется в интервале длины волны или периода колебаний таким образом, что её средняя величина остается постоянной и равной
фотона действительно изменяется в интервале длины волны или периода колебаний таким образом, что её средняя величина остается постоянной и равной  .
.

Рис. 11. а) - график скорости центра масс фотона;
b) - зависимость изменения касательной 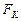 силы инерции, действующей на центр масс
силы инерции, действующей на центр масс
светового фотона в интервале одного колебания 
Поскольку сила инерции направлена противоположно ускорению, то касательная сила инерции 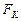 , действующая на центр масс фотона, запишется так
, действующая на центр масс фотона, запишется так
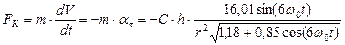 . (46)
. (46)
Несмотря на сложность переменной составляющей математической модели (46), касательная сила инерции, действующая на центр масс фотона, изменяется синусоидально (рис 11, b). Это значит, что она и генерирует прямолинейное движение фотона.
Нормальная составляющая силы инерции, действующей на центр масс фотона (центробежная сила инерции) определиться по формуле
 (47)
(47)
Результирующая сила инерции 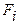 , действующая на центр масс фотона, будет равна
, действующая на центр масс фотона, будет равна
 (48)
(48)
Таким же образом определяются силы, действующие на центры масс каждого из шести магнитных полей фотона.
Уравнения движения центра масс 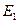 одного из магнитных полей фотона относительно подвижной системы отсчета
одного из магнитных полей фотона относительно подвижной системы отсчета  будут иметь вид (рис. 9):
будут иметь вид (рис. 9):
 ; (49)
; (49)
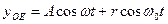 . (50)
. (50)
Уравнения абсолютного движения центра масс одного электромагнитного или магнитного поля фотона, то есть движения относительно неподвижной системы отсчета  принимают вид:
принимают вид:
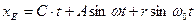 ; (51)
; (51)
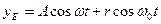 . (52)
. (52)
Это – уравнения волнистой циклоиды. Они позволяют легко определить все кинематические характеристики центров масс магнитных полей фотона.
Таким образом, выведены, постулированные раннее математические модели квантовой механики (1, 3, 4, 5, 6, 7, 8, 9, 11, 12 и 15, 16), описывающие поведение фотона. Далее, при анализе других физических явлений, в которых явно проявляется поведение фотонов, мы получим аналитически остальные и многие другие, в том числе и новые математические модели.
Итак, мы оставляем в покое почти все математические формулы, которые давно применяют для описания поведения фотона в различных экспериментах. В этом смысле у нас нет ничего нового, мы только подтвердили достоверность этих формул и дополнили их уравнениями (42) и (43), описывающими движение центра масс фотона в рамках аксиомы Единства пространства – материи – времени. Теперь у нас есть основания утверждать, что гипотезы индийского физика Бозе и английского Алана Холдена уверенно идут к пьедесталу научных постулатов.
Поскольку основные математические модели, описывающие главные характеристики фотона, выведены аналитически из анализа движения его модели, то это является веским основанием для использования этой модели при интерпретации результатов всех экспериментов, в которых участвуют фотоны. Количество таких экспериментов неисчислимо, поэтому мы будем рассматривать лишь те из них, которые носят обобщающий характер. Самая большая совокупность экспериментальных данных, в которых зафиксировано поведение фотонов – шкала электромагнитных излучений, представленная в таблицах 2, 3, 4.
Мы будем обращаться к этим таблицам при интерпретации почти всей совокупности экспериментов с участием фотонов, а сейчас определим лишь интервал изменения длины волны фотонов.
Длина волны электромагнитного излучения изменяется в интервале  (табл. 2-4). Минимальная величина этого интервала принадлежит гамма фотону, а максимальная - низкочастотному диапазону излучения. Величины эти установлены экспериментально и у нас нет оснований сомневаться в их достоверности. Но, как мы уже отметили, у нас есть основания сомневаться в том, что самый большой фотон имеет длину волны
(табл. 2-4). Минимальная величина этого интервала принадлежит гамма фотону, а максимальная - низкочастотному диапазону излучения. Величины эти установлены экспериментально и у нас нет оснований сомневаться в их достоверности. Но, как мы уже отметили, у нас есть основания сомневаться в том, что самый большой фотон имеет длину волны 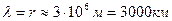 .
.
Материальная плотность базового кольца  фотона, соответствующего минимальной длине волны
фотона, соответствующего минимальной длине волны 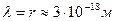 (табл. 2), равна
(табл. 2), равна
 (53)
(53)
Материальная плотность базового кольца фотона, соответствующего максимальной длине волны электромагнитного излучения  , равна
, равна
 (54)
(54)
Трудно представить фотон (с базовым радиусом  ), движущийся со скоростью света, имея материальную плотность кольца
), движущийся со скоростью света, имея материальную плотность кольца  (54).
(54).
Вряд ли возможно формирование ньютоновских и магнитных сил при такой небольшой материальной плотности базового кольца фотона (54). Поэтому должен существовать предел максимальной длины волны 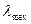 или максимального радиуса
или максимального радиуса 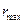 и минимальной массы
и минимальной массы  фотона.
фотона.
Поскольку температура Вселенной близка к абсолютному нулю, то её формирует максимальная совокупность фотонов с максимальной длиной волны. Мы убедимся в этом при анализе спектра Вселенной. А сейчас отметим ещё раз, поскольку тепловую энергию и температуру формируют фотоны, то 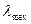 соответствует самой низкой температуре, существующей в Природе, экспериментальное значение которой равно, примерно,
соответствует самой низкой температуре, существующей в Природе, экспериментальное значение которой равно, примерно, 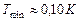 . Длина волны совокупности фотонов, формирующих эту температуру, определяется по формуле Вина (14).
. Длина волны совокупности фотонов, формирующих эту температуру, определяется по формуле Вина (14).
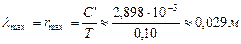 . (55)
. (55)
Фотоны с такой длиной волны соответствуют реликтовому диапазону (табл. 2-4). Их масса равна
 . (56)
. (56)
Плотность материального кольца такого фотона будет равна
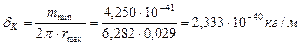 (57)
(57)
Таким образом, в Природе нет фотонов с длиной волны или радиусом, намного большим 0,029м. Конечно, эта величина будет ещё уточняться, но в любом случае она будет иметь значения, близкие к 0,029м.
Итак, фотонная шкала, так называемых, электромагнитных излучений (табл. 2, 3, 4) начинается с реликтового диапазона. Минимальную энергию  , минимальную массу
, минимальную массу  и минимальную частоту
и минимальную частоту  , но максимальную длину волны
, но максимальную длину волны 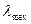 (или радиус
(или радиус  ) имеет инфракрасный фотон в реликтовом диапазоне:
) имеет инфракрасный фотон в реликтовом диапазоне:
 ; (58)
; (58)
 ; (59)
; (59)
 (60)
(60)
 (61)
(61)
Максимальную энергию  , максимальную массу
, максимальную массу  и максимальную частоту
и максимальную частоту  , но минимальную длину волны
, но минимальную длину волны  (или радиус
(или радиус  ), имеет гамма-фотон:
), имеет гамма-фотон:
 ; (62)
; (62)
 ; (63)
; (63)
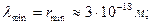 (64)
(64)
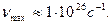 (65)
(65)
Как видно, самый маленький фотон - гамма-фотон, а самый большой фотон - инфракрасный фотон реликтового диапазона.
Таким образом, максимальная длина волны единичных фотонов соответствует реликтовому диапазону, а минимальная - гамма диапазону (табл. 2, 3, 4). От реликтового диапазона до гамма диапазона длина волны фотона уменьшается, примерно, на 15 порядков, а частота увеличивается на столько же.
Сразу возникает вопрос: какое электромагнитное образование формирует электромагнитное излучение с длиной волны, больше длины волны реликтового диапазона? Ответ на этот вопрос следует из гипотез индийского ученого Бозе и английского физика Алана Холдена, представленных на рис. 3.
Как видно (рис. 3), фотоны могут двигаться в виде отделённых друг от друга совокупностей, которые проявляют свойства, присущие волнам. Поэтому у нас есть основания назвать импульсы совокупностей фотонов фотонными волнами (рис. 3). Шарики - это фотоны. Расстояние между импульсами фотонов (шариков) равно длине волны 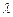 , так называемого, электромагнитного излучения, а длина волны каждого отдельного фотона значительно меньше. Она, как мы уже показали, определяет область его локализации в пространстве.
, так называемого, электромагнитного излучения, а длина волны каждого отдельного фотона значительно меньше. Она, как мы уже показали, определяет область его локализации в пространстве.
Так как фотоны всех диапазонов движутся с одной и той же скоростью  и так как они же формируют и волны, правильно называемого фотонного излучения (рис. 3), то скорость фотонного излучения всех диапазонов одна и та же. Сразу обратим внимание на то, что понятие «шкала электромагнитных излучений» не соответствует физическому содержанию её структуры (рис. 3), поэтому у нас есть все основания заменить название «шкала электромагнитных излучений» названием «шкала фотонных излучений» или просто «фотонная шкала».
и так как они же формируют и волны, правильно называемого фотонного излучения (рис. 3), то скорость фотонного излучения всех диапазонов одна и та же. Сразу обратим внимание на то, что понятие «шкала электромагнитных излучений» не соответствует физическому содержанию её структуры (рис. 3), поэтому у нас есть все основания заменить название «шкала электромагнитных излучений» названием «шкала фотонных излучений» или просто «фотонная шкала».
Полученная информация делит фотонную шкалу на два класса: фотонный и волновой. Фотоны - единичные магнитные образования, излучаются электронами атомов и протонами ядер. Совокупность фотонов, излученных электронами атомов или протонами ядер, формирует фотонное поле. Оно может быть непрерывным или импульсным, то есть волновым (рис. 3). Мы живём в этом поле, как рыбы в воде и не замечаем этого.
Информация о фотоне проясняет причину сходимости результатов решений уравнений Максвелла с рядом экспериментальных данных. Дело в том, что электроны любой антенны возбуждаются фотонами среды непрерывно, формируя её температуру и фоновый шум. Управляемое воздействие на этот процесс заставляет эти же электроны излучать импульсы фотонов с другими радиусами в виде волн (рис. 3), которые возбуждают у антенны приемника импульсы тока, такие же, какие ошибочно приписываются действию максвелловской электромагнитной волны (рис. 2). Если волна, излученная антенной или любым другим источником, состоит из фотонов (рис. 3), то величина генерируемого тока будет зависеть от количества фотонов, попавших на неё, и от их индивидуальной энергии, но не от напряженности, выдуманного для этого случая электрического и магнитного полей. Это доказывает прибор ИГА-1 (рис. 12). Имея чувствительность 100 пико вольт, он принимает естественные излучения с частотой 5 кГц и длиной волны 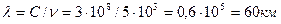 на антенну диаметром 30 мм. Уравнения Максвелла работают лишь в условиях, когда длина волны излучения соизмерима с размером антенны приёмника. Это - убедительное доказательство того, что электромагнитные волны Максвелла (рис. 2) не являются носителями излучений.
на антенну диаметром 30 мм. Уравнения Максвелла работают лишь в условиях, когда длина волны излучения соизмерима с размером антенны приёмника. Это - убедительное доказательство того, что электромагнитные волны Максвелла (рис. 2) не являются носителями излучений.

Рис. 12. Прибор ИГА – 1. Разработчик: Кравченко Ю. П.
При поиске ответа на вопрос: почему уравнения Максвелла в ряде случаев дают результат, близкий к экспериментальному, надо учесть, что при численном решении этих уравнений используется процедура разложения в ряд Фурье. Однако, если учесть, что уравнения Максвелла описывают процессы, близкие к синусоидальным, то их можно заменить уравнением синусоиды с соответствующими параметрами и привести результат эксперимента, разложенный в ряд Фурье, к результату, описываемому синусоидой с такими же параметрами, какие дают уравнения Максвелла.
Таким образом, сходимость результатов решения уравнений Максвелла с экспериментальными данными – следствие синусоидального характера фотонной волны (рис. 3). Туманный физический смысл уравнений Максвелла надёжно прикрывал ошибочную интерпретацию структуры, так называемого, электромагнитного излучения более 100 лет.
Дата добавления: 2020-11-18; просмотров: 434;











