Корпускулярная теория фотона

Фотон – локализованное (ограниченное) в пространстве образование, которое переносит энергию и информацию. Всё, что мы видим на этой странице, приносят в наши глаза фотоны. Мы хорошо различаем контуры букв, запятые, точки. Это значит, что каждый фотон из их совокупности, несущей в наши глаза образы, например, точек, должен иметь размер значительно меньше точки. Тогда их совокупность передаст чёткую информацию об объекте, от которого они отразились.

Известно, что длина волны световых фотонов изменяется в интервале . Это значит, что размер каждого светового фотона, примерно, в 10000 раз меньше миллиметра. Он остаётся пока самым загадочным творением Природы. Долго не удавалось раскрыть структуру фотона путем анализа необозримой экспериментальной информации о его поведении с помощью физических теорий, существовавших в ХХ веке. Главная причина такого состояния, как мы сейчас увидим, заключалась в том, что в реальной действительности фотон ведет себя в рамках аксиомы Единства пространства - материи - времени, а физики пытались анализировать его поведение с помощью теорий, которые работают за рамками этой аксиомы.

Начнем с анализа математических моделей, которые описывают основные характеристики фотонов, установленные экспериментально. Первыми из них являются математические модели, определяющие их энергию. В математическую модель для определения энергии фотона 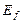, входят: масса 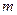фотона и постоянная скорость его прямолинейного движения в пространстве, равная скорости света 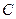- первой константе, описывающей поведение фотонов.

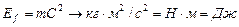. (1)

В соответствии с законами классической физики, а точнее, классической механики, кинетическая энергия тела, движущегося прямолинейно с постоянной скоростью 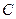, равна

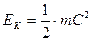. (2)

Причина различий в математических моделях (1) и (2) проясняется, если предположить, что фотон имеет форму кольца, которое движется прямолинейно и вращается так, что поступательные и окружные скорости его точек равны 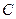(рис. 4, а).

Рис. 4. Схемы: а) качения кольца; b) волны

Так как в прямолинейном движении кольца с радиусом относительно системы отсчета ХОУ (рис. 4) со скоростью 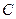и во вращательном движении относительно геометрического центра 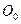с угловой скоростью (частотой) скорость любой точки 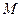кольца равна 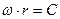, то сумма кинетических энергий прямолинейного и вращательного движений кольца равна

. (3)

Обращаем внимание на тот факт, что в формуле (3) - момент инерции кольца, а - угловая скорость или угловая частота вращения кольца (рис. 4, а).

Следующее важное уточнение заключается в том, что - момент инерции кольца, не имеющего размера в поперечном сечении. Фактически это момент инерции окружности. Но так как окружность имеет только геометрический размер и не является материальным телом, то окружность, имеющую массу, назвали кольцом. Поэтому, в дальнейшем под понятием материальная окружность мы будем понимать кольцо, имеющее радиус, но не имеющее размера в поперечном сечении, и назовём его базовым кольцом.

Итак, первый этап анализа показывает, что фотон представляет собой в первом приближении кольцо. Однако, этого мало, чтобы такую информацию считать соответствующей реальности. Нужны дополнительные доказательства. Они следуют из второй математической модели, определяющей энергию фотона. Она постулирована Максом Планком в 1900г.

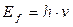, (4)

где 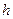- постоянная Планка – вторая константа, определяющая энергию единичного фотона; 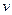- линейная частота фотона.

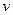Известно, что угловая и линейная частоты, связаны зависимостью

. (5)

Линейная частота 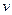следует из периода 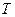волны и связана с ним зависимостью (рис. 4, b)

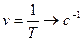. (6)

На рис. 4, b видно, что если фотон – волна длиною , то скорость его прямолинейного движения определяется зависимостью

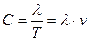. (7)

Таким образом, из приведенного анализа следует, что фотон - это частица и волна одновременно. Эту совокупность свойств фотоны проявляют и в явлениях дифракции и интерференции, формируя у нас загадочные представления об их поведении. Дальше мы раскроем эту загадку, а сейчас обратим внимание на то, что формулы (1), (3) и (4) отражают явные корпускулярные свойства фотона, но присутствие в формуле (4) линейной частоты 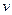, вместо угловой - , указывает на то, что фотон, являясь частицей, описывает в движении волну (рис. 4, b). Для нас это пока странное движение, но дальше мы познакомимся с ним в деталях.

Анализируя соотношения (1) и (4), видим, что:

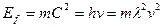; (8)

. (9)

Обратим внимание на размерность константы Планка (9). Строго говоря, эта размерность не содержит ясного физического смысла. Если бы она была такой 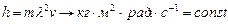, то в классической механике она имеет названия: момент количества движения и кинетический момент. В классической физике эту размерность называют момент импульса или угловой момент. Дальше мы увидим, что в размерности формулы (9) присутствует и радиан, но он спрятан очень глубоко. Из этого автоматически следует, что постоянная Планка описывает вращательные процессы, но присутствие в её выражении (9) длины волны указывает на то, что она описывает волновой процесс. Это фундаментальное противоречие – главный источник заблуждений физиков ХХ века о структурах элементарных частиц.

Указанное противоречие сформировало представление о том, что законы классической физики не работают в микромире. Там господствует так называемая квантовая теория, основы которой заложил Макс Планк в начале ХХ века, введя в описание излучения абсолютно черного тела знаменитую константу 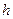(9), которая была названа его именем. С тех пор она вошла во все математические модели, описывающие поведение всех обитателей микромира.

Поскольку в то время господствовали волновые представления об излучении, то Макс Планк, опасаясь обвинений в механицизме, назвал свою константу квантом наименьшего действия. Отсутствие физической сути размерности (9) в названии «квант наименьшего действия» сдерживало понимание физики процессов и явлений, которые описываются с помощью постоянной Планка.

Присутствие в формуле (9) длины волны излучения 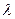спасало идею его волновой природы, но явно противоречило размерности постоянной Планка, из которой следовало, что она описывает вращательный процесс. Чтобы избавиться от этого противоречия, достаточно было поставить элементарный вопрос: какой закон управляет постоянством константы Планка? Она ж ведь не может быть постоянной без причины? Ответ на этот вопрос можно получить лишь при одном условии: длины волн 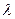всех элементарных образований микромира, описываемых с помощью постоянной Планка, равны радиусам их вращения. Эта гипотеза, как мы увидим, быстро завоёвывает статус научного постулата.

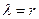. (10)

При этом сразу раскрывается закон, управляющий постоянством константы Планка в её новой записи

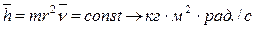. (11)

Прежде всего, - момент инерции кольца. Мы уже условились называть его базовым кольцом элементарных частиц. Поскольку момент инерции базового кольца умножается не на угловую частоту , а на линейную 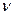, то это означает, что кольцо совершает такие импульсные вращения в интервале каждой длины волны 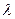, при которых сумма моментов сил, действующих на него, равна нулю. Поэтому кинетический момент базового кольца остаётся постоянным. Это и есть закон, управляющий постоянством константы Планка. Он гласит: если сумма моментов внешних сил, действующих на вращающееся тело равна нулю, то его Кинетический момент (момент импульса) остаётся постоянным по величине и направлению. Из этого автоматически следует, что постоянная Планка 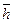- величина векторная. Дальше мы увидим, что это фундаментальное следствие раскрывает практически все загадки микромира и, самое главное, позволяет описывать процессы формирования структур фотонов всей шкалы излучений, процессы формирования электрона, протона и нейтрона, а также процессы формирования, ядер, атомов, молекул и кластеров.

Вектор 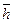направлен вдоль оси вращения базового кольца так, что если смотреть с его острия, то вращение будет направлено против хода часовой стрелки (рис. 5).

Если постоянная Планка 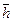имеет размерность кинетического момента и если с ее помощью описывать поведение элементарных частиц, то они обязательно должны вращаться вокруг своих осей. Вектор константы Планка 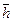в этом случае называют спином.

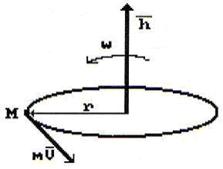
Рис. 5. Схема к определению понятия кинетический момент 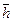кольца

Дальше мы увидим, что большая часть математических моделей, описывающих поведение фотонов, выводится из законов классической физики, а точнее – из законов классической механики. Поэтому в дальнейшем размерность постоянной Планка мы будем называть «кинетический момент».

Обратим внимание ещё раз на то, что момент инерции кольца в формуле (11) умножается не на угловую частоту его вращения, а на линейную частоту 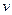. Наиболее близкое понятие для характеристики произведения момента инерции базового кольца на линейную частоту - импульс момента инерции базового кольца. Из этого следует, что фотон имеет такую структуру, которая совершает импульсные вращения в интервале каждой длины волны. Это возможно, если фотон имеет не форму кольца, а форму вписанного в него многоугольника. Из равенства (10) следует, что это - шестигранный многоугольник (рис. 6, b).

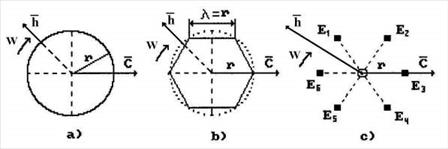
Рис. 6. К выявлению структуры фотона

Поскольку длина волны 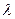импульса момента инерции базового кольца равна радиусу его вращения 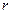, то угловой интервал каждого импульса шестигранника (рис. 6, b) равен 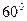и он делает за один оборот шесть импульсов. Так как 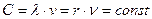, то из автоматически следует третья константа

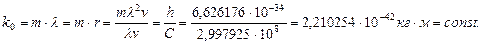(12)

Из размерности константы (12) следует физический закон: произведение масс фотонов на длины их волн или радиусы – величина постоянная. В системе СИ нет названия константе с такой размерностью, поэтому назовем её константой локализации элементарных частиц.

Легко представить реализацию константы локализации (12), если фотон – кольцо (рис. 4, а, 5) и невозможно это сделать, если фотон – волна (рис. 2, 4, b).

Обратим внимание на то, что в технической системе единиц константа (12) имеет другой физический смысл – момент 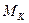силы. Это означает, что момент сил, действующих во внутренней структуре фотона, - величина постоянная для фотонов всех диапазонов излучений

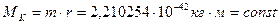. (13)

Отметим, что появление постоянного момента сил, вращающего фотон, возможно лишь только в том случае, если векторы сил, генерирующих этот момент, не будут пересекать геометрический центр модели фотона, то есть - будут нецентральными силами.

Итак, формированием электромагнитной структуры фотона управляют пока три константы: скорость их движения 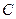, кинетический момент 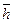и константа локализации 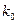или постоянный момент силы 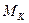, вращающий фотон. Вполне естественно, что этот момент генерируют внутренние силы фотона и у нас появляются основания предположить, что эти силы и обеспечивают его прямолинейное движение с постоянной скоростью .

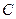При анализе существующих математических моделей, описывающих поведение фотонов в рамках классических законов, мы пришли в первом приближении к кольцевой модели фотона (рис. 6, а), а во втором – к его шестигранной модели (рис. 6, b). В третьем приближении мы должны получить магнитную модель фотона.