Растяжение (сжатие)

К стержню (бруску) длиной l и площадью поперечного сечения S прикладывается сила F, направленная перпендикулярно сечению (рис. 11.1). В результате этого в теле возникает механическое напряжение о, которое в данном случае характеризуется отношением силы к площади поперечного сечения стержня (малое изменение площади поперечного сечения не учитывается):

В СИ механическое напряжение измеряется в паскалях (Па).

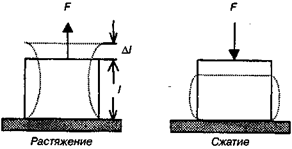
Рис. 11.1.Деформации растяжения и сжатия

Под действием приложенной силы длина стержня изменяется на некоторую величину ∆l, которая называется абсолютной деформацией. Величина абсолютной деформации зависит от первоначальной длины стержня, поэтому степень деформации выражают через отношение абсолютной деформации к первоначальной длине. Это отношение называется относительной деформацией (ε):

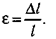
Относительная деформация — величина безразмерная. Иногда

ее выражают в процентах: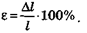

При небольшой величине относительной деформации связь между деформацией и механическим напряжением выражается законом Гука:

где Е — модуль Юнга, Па (модуль продольной упругости).

При упругой деформации напряжение прямо пропорционально величине деформации.

Модуль Юнга численно равен напряжению, увеличивающему длину образца в два раза (практически разрушение образцов наступает при значительно меньших напряжениях). В табл. 11.1 представлены значения модулей упругости некоторых материалов.

В большинстве случаев при растяжении или сжатии степень деформации в различных сечениях стержня различна. Это можно увидеть, если на поверхность тела нанести квадратную сетку. После деформирования сетка исказится. По характеру и величине этого искажения можно судить о распределении напряжения вдоль образца (рис. 11.2).

Таблица 11.1