Промежутки знакопостоянства функции. Нули функции
Числовые промежутки, на которых функция сохраняет свой знак (т.е. 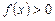 или
или 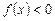 ) называются промежутками знакопостоянства.
) называются промежутками знакопостоянства.
Значения аргумента 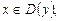 при которых
при которых 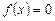 , называются нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.
, называются нулями функции. Нули функции – это точки пересечения графика функции с осью Ох.
Пример 1.Найти область определения функции
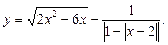
Решение.
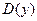 :
: 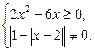 (1)
(1)
Найдем соответствующее 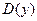 множество точек.
множество точек.
Неравенство 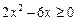 равносильно неравенству
равносильно неравенству
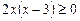 . Решая его, получаем (рис.1)
. Решая его, получаем (рис.1)

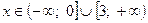 .
.
Условие
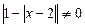 Рис.1
Рис.1
означает, что
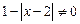 , т.е.
, т.е. 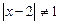 .
.
Приходим к заключению, что
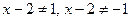 . Получаем
. Получаем 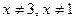 .
.
Таким образом система (1) равносильна системе
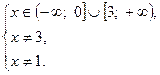
Значит 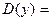
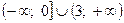 .
.
Пример 2.Найти множество значений функции
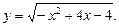
Решение.
Найдем область определения функции.
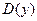 :
: 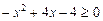 ;
;
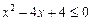 ;
;
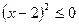 .
.
Последнее условие выполняется только для 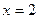 . Вычисляем значение функции в этой точке:
. Вычисляем значение функции в этой точке: 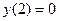 .
.
Значит 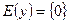 .
.
Пример 3.Исследовать функцию на четность:
1) 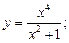 2)
2) 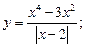 3)
3) 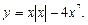
Решение.
1. Замечаем, что для функция 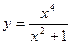 имеет
имеет 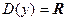 . Значит, функция определена на симметричном множестве.
. Значит, функция определена на симметричном множестве.
Рассмотрим ее значение для 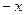 :
:
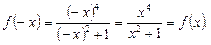
Поскольку выполняются оба условия четной функции, заключаем, что функция 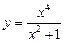 – четная.
– четная.
2. Функция 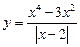 имеет
имеет 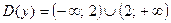 .
.
Так как 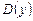 не является симметричным множеством, второе условие проверять нет необходимости. Эта функция не обладает свойством четности.
не является симметричным множеством, второе условие проверять нет необходимости. Эта функция не обладает свойством четности.
3. Очевидно, что функция  имеет
имеет 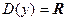 , т.е. определена на симметричном множестве и для нее
, т.е. определена на симметричном множестве и для нее
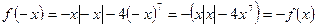 .
.
Оба условия нечетной функции выполняются, а потому данная функция является нечетной.
Пример 4.Пусть 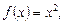 где
где 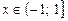 . Причем, функция имеет период 2. Построить ее график.
. Причем, функция имеет период 2. Построить ее график.
Решение.
Построим график данной функции на 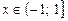 (рис. 2).
(рис. 2).
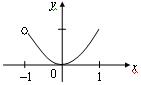
Рис. 2
Исходя из определения периодической функции должно выполняться условие: 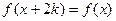 , где
, где 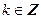 .
.
Строим ее график, продолжая по периоду (рис. 3).
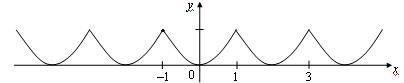
Рис. 3
Пример 5.Используя определение монотонной функции, найти значения а, при которых функция 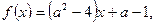 где
где 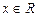 монотонно возрастает.
монотонно возрастает.
Решение.Пусть 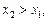
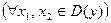 . Функция монотонно возрастает, если выполняется
. Функция монотонно возрастает, если выполняется 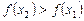 или
или 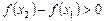 . Это означает, что
. Это означает, что
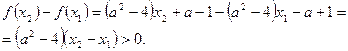
Поскольку 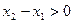 , последнее неравенство выполняется, если
, последнее неравенство выполняется, если 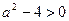 , т.е
, т.е 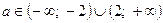 .
.
Таким образом, функция возрастает для 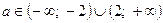 .
.
Пример 6.Дана функция
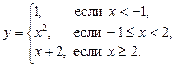
Определить промежутки знакопостоянства функции, нули функции. Построить график данной функции.
Решение. Так как на каждом из данных промежутков аналитические выражения, задающие функцию, определены в каждой точке, следовательно 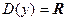 .
.
1. Исследуем функцию при 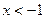 . На данном промежутке функция принимает значение равное 1, т.е. она знакоположительна и нулей функции нет.
. На данном промежутке функция принимает значение равное 1, т.е. она знакоположительна и нулей функции нет.
2. Пусть 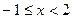 .
.
При таком условии функция задается формулой 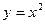 и
и 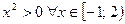 . Функция знакоположительна. Здесь она имеет нуль
. Функция знакоположительна. Здесь она имеет нуль 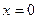 .
.
3. Пусть 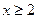 .
.
Очевидно, что при этом условии 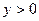 , т.к.
, т.к. 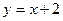 . Нулей функции на этом промежутке нет.
. Нулей функции на этом промежутке нет.
Построим график:
Если 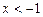 , строим часть прямой линии
, строим часть прямой линии 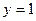 ;
;
Если 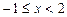 – часть параболы
– часть параболы 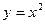 ;
;
Если 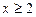 – часть прямой
– часть прямой 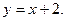
Получили график заданной функции (рис.4).
 |
Рис. 4
Таким образом, функция знакоположительна 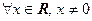 ; имеет нуль
; имеет нуль 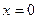 .
.
Задания
I уровень
1.1. Найдите область определения функции:
1) 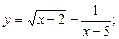 2)
2) 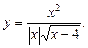
1.2. Исследуйте функцию на свойство четности:
1) 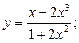 2)
2) 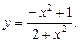
1.3. Найдите множество значений функции 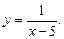
1.4. Для функции 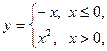 определите промежутки монотонности, нули, промежутки знакопостоянства. Постройте график функции.
определите промежутки монотонности, нули, промежутки знакопостоянства. Постройте график функции.
II уровень
2.1. Найдите ОДЗ функции:
1) 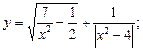 2)
2) 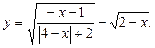
2.2. Найдите множество значений функции:
1) 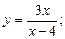 2)
2) 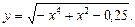
2.3. Задайте функцию аналитически:
1) линейную, если 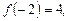
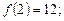
2) квадратичную, если 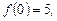
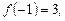
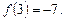
2.4. Исследуйте функцию на четность:
1) 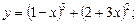 2)
2) 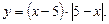
2.5. Докажите, что функция:
1) 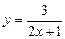 убывает на
убывает на 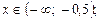
2) 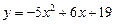 возрастает на
возрастает на 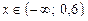
2.6. Исследуйте функцию 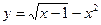 на монотонность.
на монотонность.
2.7. Пусть 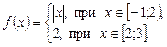
Известно, что 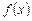 имеет период Т = 4. Постройте график функции.
имеет период Т = 4. Постройте график функции.
III уровень
3.1. Исследуйте функцию на четность. Найдите ее нули:
1) 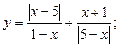 2)
2) 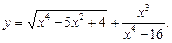
3.2. Найдите нули функции, промежутки знакопостоянства, промежутки монотонности:
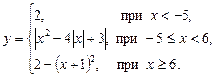
Постройте график.
3.3. Дана функция 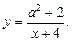 Найдите промежуток на котором она убывает.
Найдите промежуток на котором она убывает.
3.4. Определите, при каком а функция 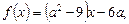
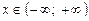 является периодической.
является периодической.
3.5. Найдите 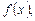 если:
если:
1) 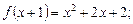 2)
2) 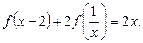
3.6. Определите, при каком значении аргумента значение функции 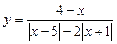 равно –1.
равно –1.
3.7. Определите при каких значениях х график функции 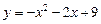 расположен выше графика функции
расположен выше графика функции 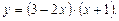
Дата добавления: 2016-07-27; просмотров: 11761;











