ПЛИН В'ЯЗКИХ РІДИН У БІОЛОГІЧНИХ СИСТЕМАХ

<2 3 456 7 8 >

Рух рідких середовищ (крові, лімфи, інтерстиціальних та клітинних рідин) у біологічних системах відіграє важливу роль, забезпечуючи умови нормальної життєдіяльності різних фізіологічних систем. Задача біофізики полягає у вивченні фізичних властивостей рідких середовищ і фізичних основ їх руху. Плин рідин відбувається під дією сил, з'ясування природи яких також є однією з важливих задач біофізики.

Рідкі середовища мають ряд специфічних властивостей, зумовлених особливостями їх молекулярної будови. Однією з найважливіших властивостей рідини є в'язкість.

В'язкість рідини

У реальних рідких середовищах на границях шарів, що рухаються, діють сили внутрішнього тертя. Можна навести чимало прикладів дії цих сил: вони є причиною падіння

тиску вздовж судини при плині крові, саме вони визначають поведінку рідини у судині, що обертається, перешкоджують рухові тіл у рідинах тощо.

Досліди свідчать про те, що сили тертя між шарами рідини, які рухаються з різними швидкостями, діють по дотичній до поверхонь цих шарів (мал. 1.7) і спрямовані таким чином, що прискорюють шар, що рухається більш повільно, і гальмують шар, який рухається швидше.

Розглянемо поведінку рідини, що знаходиться між двома пластинами, одна з яких нерухома, а інша під дією прикладеної до неї сили F рівномірно рухається зі швидкістю υ (мал. 1.7). Дія дотичного зсуваючого напруження σ_τ= - F_T /S викликає деформацію зсуву, причому відносний зсув за одиницю часу γ = dv/dy , який називають градієнтом швидкості, виявляється пропорційним до прикладеного зсувного напруження:

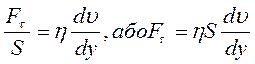. (1.8)

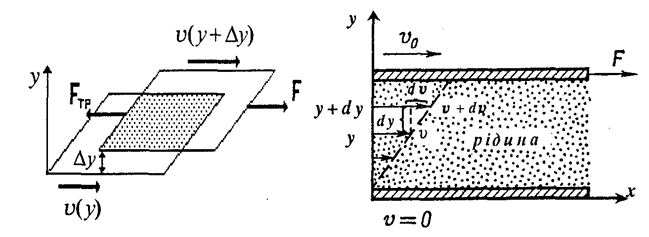
Мал. 1.7. Сила тертя між шарами рідини. Мал. 1.8. Профіль швидкостей.

Рівняння (1.8), відоме як рівняння Ньютона, описує явище внутрішнього тертя. Таким чином, профіль швидкостей, який ми спостерігаємо у цьому випадку (мал. 1.8), обумовлений тим, що між шарами реальної рідини, що тече, діють сили внутрішнього тертя F, які пропорційні до площі S шарів, що дотикаються, та градієнта швидкості dυ/dy у напрямку, перпендикулярному до напрямку плину рідини. Коефіцієнт пропорційності η в рівнянні Ньютона зветься коефіцієнтом в'язкості (точніше кажучи, зсувної в'язкості) і дорівнює силі внутрішнього тертя, що діє на одиницю площі поверхні шару при градієнті швидкості, який дорівнює одиниці.

Розмірність коефіцієнта в'язкості η у системі СІ [Па*с]. Досить часто використовується ще й позасистемна одиниця в'язкості Пуаз (П), яка зв'язана з Па*с співвідношенням 1П= 0.1 Па*с. Так, в'язкість дистильованої води при кімнатній температурі дорівнює приблизно 10^-3 Па*с = 10^-2 П, тобто Цводи ≈ 1 мПа*с = 1сП.

Зручно користуватися безрозмірним коефіцієнтом в'язкості, що зветься відносною в'язкістю η_відн . Відносна в'язкість дорівнює відношенню коефіцієнта в'язкості даної рідини до коефіцієнта в'язкості дистильованої води при одній і тій самій температурі:

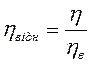(1.9)

У гідродинаміці користуються також і кінематичною в'язкістю v рідини, що являє собою відношення коефіцієнта в'язкості до густини

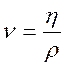(1.10)

Кінематична в'язкість v має розмірність [v] = м²/с. В'язкість рідини є динамічна властивість, залежить від природи рідини, температури і для багатьох рідин також від умов плину.

Моделі рідин. Описуючи рух рідких середовищ, використовують різні моделі рідин. Найбільш простою є модель ідеальної рідини, яка не підлягає стисненню (ρ= const) і в ній відсутні сили внутрішнього тертя (η= 0). Ця модель використовується для отримання найбільш простих рівнянь руху рідини. Неідеальні рідини, в яких сили внутрішнього тертя описуються рівнянням Ньютона, звуться ньютонівсь-

кими. Для ньютонівських рідин коефіцієнт в'язкості η залежить лише від температури та природи рідини і не залежить від умов плину. До ньютонівських рідин можна віднести воду, розчини електролітів, ртуть, гліцерин, спирти. Існують рідини, коефіцієнт в'язкості яких залежить від умов плину, а саме, змінюється із зміною швидкості деформації зсуву dυ/dy внаслідок перебудови внутрішньої структури, обумовленої напруженням зсуву при плині рідини. Такі рідини звуться неньютонівськими. До них відносять розчини білків, полімерів, деякі суспензії.

Описуючи динаміку руху біологічних рідин, розглядають умови їх плину і, залежно від них, обирають ту чи іншу модель рідини - від ідеальної до реальної.

1.2.2. В'язкість крові

Кров являє собою приклад складної за своїм вмістом рідини. Вона є суспензією форменних елементів (еритроцитів, лейкоцитів, тромбоцитів) у водному колоїдному розчині - плазмі, сумарна концентрація білків у якій становить 6-9%. Експеримент виявив суттєву залежність в'язкості крові від її складу, що визначається показником гематокриту Не (мал. 1.9а), який дорівнює відношенню об'єму форменних елементів V_ф до об'єму плазми крові V_пл:

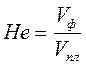(1.11)

Оскільки об'єм форменних елементів в основному припадає на еритроцити, показник гематокриту характеризує вміст еритроцитів у крові.

Як свідчить наведена на малюнку залежність η_відн = = f(Не), в'язкість крові змінюється у досить широкому діапазоні по відношенню до норми (N). Вона зростає при поліцитемії і зменшується при анемії.

Відомо декілька емпіричних формул, що зв'язують коефіцієнт в'язкості крові з показником гематокриту:

1 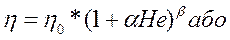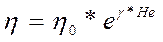(1.12)

де η_о - в'язкість плазми, α, β, γ- емпіричні константи, значення яких залежить від концентрації та форми суспен-зованих елементів.

Дослідження залежності в'язкості крові від швидкості деформації зсуву (градієнта швидкості) свідчать про те, що кров не є ньютонівською рідиною. При великих градієнтах швидкості (наприклад, в артеріальних судинах) в'язкість крові наближається до в'язкості води, у той час як при малих значеннях швидкості деформації зсуву в'язкість у п'ять і більше разів перевищує в'язкість води (мал. 1.9б).

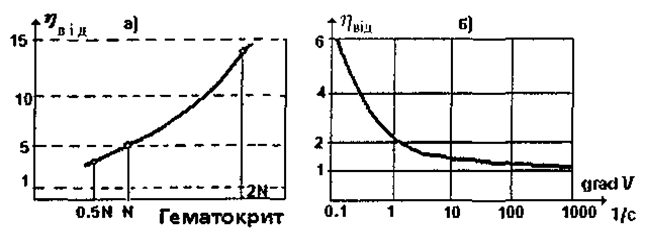
Мал. 1.9. Зміна в'язкості крові при зміні: а) форменного складу крові, б) швидкості деформації зсуву.

Величина відносної в'язкості крові може бути використана у діагностиці захворювань (див. табл. 1.1). Залежність коефіцієнта в'язкості від градієнта швидкості dυ/dy обумовлена здатністю еритроцитів до агрегації - утворенню "монетних стовпчиків" та їх конгломератів. Із збільшенням градієнта швидкості стовпчики руйнуються, і коефіцієнт в'язкості зменшується внаслідок дезагрегації та деформації еритроцитів.

Таблиця 1.1.

Відносна в'язкість крові Результат

4.2-6.0 Норма

<2.0 Анемія

>10.0 Поліцитимія

Зменшення в'язкості крові при її переході з венозного русла в артеріальне фізіологічне виправдане. У цьому випадку значно зменшуються витрати м'язової енергії міокарду на просування крові вздовж артеріального русла, в якому величини швидкостей деформації зсуву (а отже і сили внутрішнього тертя) досить значні (вони у сотні разів перебільшують значення останніх у венозній ділянці судинної системи).

1.2.3. В'язко-пружні властивості біологічних тканин

Біологічні структури (м'язи, судини, сухожилля, тканини легенів, шкіра тощо) являють собою в'язко-пружні системи, їх поведінка вивчається на моделях, що вміщують пружні (Е) та в'язкі (η) елементи, у деяких випадках до них додають і елементи зовнішнього тертя (К).

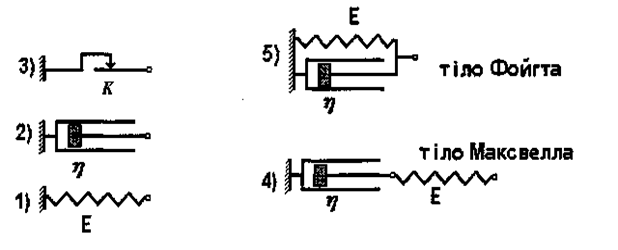
Мал. 1.10. Механічні моделі тканин: 1) пружний елемент; 2) в'язкий елемент; 3) елемент внутрішнього тертя; 4) послідовне з'єднання в'язкого та пружного елементів; 5) паралельне з'єднання в'язкого та пружного елементів.

Пружний елемент являє собою ідеальну пружину, для якої виконується закон Гука. В'язкий елемент може бути поданий у вигляді циліндра, який заповнений в'язкою рідиною з нещільним поршнем. Для витягування поршня необхідно прикласти деяку зовнішню силу, яка компенсує сили в'язкого тертя, що виникають при плині рідини крізь зазор.

Напруження, що створюються цими елементами під дією зовнішніх сил, дорівнюють:

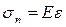· для пружного елементу;

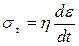· для в’язкого елементу;

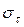· ~ KF_n для елементу зовнішнього тертя при силі нормального тиску F_n і коефіцієнті тертя К.

Для відтворення механічних властивостей біологічних тканин використовують моделі, що складаються з цих елементів. Найпростішими моделями є тіло Максвелла і тіло Фойгта, що являють собою послідовне і паралельне з'єднання пружного та в'язкого елементів (див. мал. 1.10). Ці моделі дозволяють відтворити такі динамічні властивості тканин, як повзучість та релаксація напруження.

Повзучість - це явище зміни з часом розмірів зразка в умовах дії постійного напруження. Якщо у біологічних тканинах швидко створити, а потім підтримувати постійним деяке напруження, то з часом відбувається поступове подовження зразка аж до розриву тканин, навіть при умові, що постійне напруження має менше значення, ніж межа міцності матеріалу. Динаміку повзучості подано на мал. 1.1 la. Зміна розмірів відбувається тим швидше, чим більше напруження, що підтримується у зразку (порівняйте криві 1, 2 та 3, для яких (σ₁ > σ₂ > σ₃).

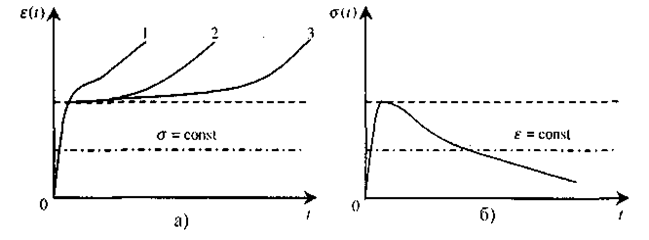
Мал. 1.11. Динамічні властивості біологічних тканин: а) повзучість - зміна деформації тіла за умови постійного напруження σ (σ₁ > σ₂ > σ₃); б) релаксація напруження - зменшення σ в умовах постійної деформації.

Релаксація напруження - явище зменшення з часом величини напруження у зразку при підтримці постійної величини деформації. Якщо швидко розтягнути зразок і, підтримуючи постійною отриману деформацію, вимірювати напруження в ньому протягом деякого часу, помітним стане його зменшення з часом (мал. 1.116). Пунктирними лініями на обох мал. 1.11 відтворено поведінку чисто пружних тіл. Релаксація напруження і повзучість суто динамічні процеси - час їх існування вимірюється секундами або хвилинами. Наприклад, для м'язів час зменшення напруження на 40% становить близько 10 секунд.

Ці процеси легко пояснюються механічними моделями, наведеними на мал. 1.10 (позиція 4). Спочатку під дією зовнішніх сил деформується пружний елемент, а потім починається "плин" в'язкого елементу, змінюється його розмір, що викликає зміну як довжини, так і напруження. За допомогою моделі Максвелла легко отримати експоненціальний закон релаксації напруження

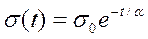, (1.13)

де α- постійна часу релаксації, σ₀ = Еε- початкове напруження.

Явище повзучості також можна описати експоненціальним законом

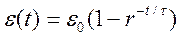(1.14)

де ε₀= σ₀/Е - початкова деформація, τ- характерний час процесу повзучості, що дорівнює відношенню коефіцієнта в'язкості і модуля Юнга. Формулу τ= η/Е легко отримати з міркувань розмірності. Дійсно, розмірність η є Па*с, a розмірність Е дорівнює Н/м² = Па. Тому єдина комбінація величин ηі Е, що має розмірність часу [τ] = с, є їх відношення η/е.

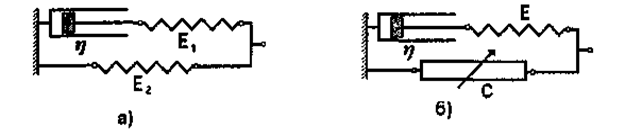
Мал. 1.12. Приклади механічних моделей біологічних тканин: а) трьохелементна модель для дослідження механічних властивостей 1в'язко-пружних тканин; б) трьохелементна модель м'язів, що включає скорочувальний елемент С.

Модель Фойгта дозволяє пояснити поступове зростання з часом напруження у зразку, якщо до тіла прикласти зусилля, що змінюється стрибкоподібне. Динаміка експоненціального зменшення напруження чи деформації відрізняється від експерименту. Кращих результатів можна досягти, якщо розглядати моделі, що включають до себе кілька пружних та в'язких елементів. Приклад однієї з таких моделей наведено на мал. 1.12. На цьому ж малюнку наведено одну з найпростіших моделей м'язів, що включає скорочувальний елемент С, котрий являє собою механохімічний конвертор, який перетворює енергію хімічних реакцій на механічну енергію. Ця механічна енергія витрачається на створення напруження і здійснення роботи по скороченню м'язів.

Наявність в'язко-пружних елементів, з'єднаних зі скорочувальними елементами, забезпечують ті гнучкі функціональні властивості, які притаманні цілому ряду фізіологічних систем (наприклад, серцево-судинній, м'язовій і ряду інших) для виконання призначених їм функцій в умовах зміни як властивостей самої системи, так і зовнішних навантажень. Це явище притаманне системам, які адаптуються. Так, зміна тонусу судин еласто-м'язового типу дозволяє реалізувати таке явище, як депонування крові, при якому значне збільшення об'єму судини можливе лише при повній релаксації стінки судини і зменшенні її пружності. Навпаки, при необхідності вигнання крові з депо об'єм судин зменшується, релаксація напруження

відбувається при інших розмірах судини, у цьому випадку зростає і модуль об'ємної пружності судин (їх тонус).

1.2.4. Основні рівняння руху рідини

Рух рідких середовищ підпорядковується тим самим законам механіки, що і рух твердих тіл та газів. У суцільному середовищі можна виділити елементарний об'єм рідини dV (чи елемент маси dm=pdV, p - густина середовища), розглянути сили, що діють на нього і записати рівняння статики (рівноваги) чи динаміки. При русі у просторі кожний такий елементарний об'єм рухається вздовж деякої траєкторії - лінії струму (мал. 1.13а,б). Дотична до будь-якої точки лінії струму збігається з напрямом вектора швидкості частинки у цій точці. Виділимо у просторі замкнений контур S. Всі лінії струму, що проходять крізь цей контур, утворюють трубку струму. Таким чином, трубка струму являє собою частину потоку рідини, обмежену лініями струму (мал. 1.1.3в).

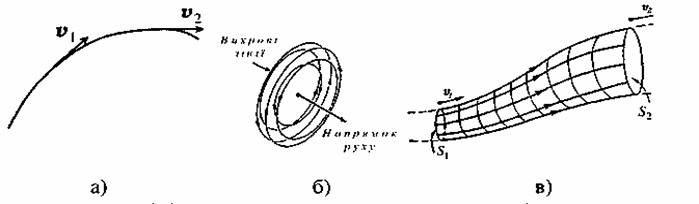
Мал. 1.13. Лінії струму при стаціонарному (а) і турбулентному плині (б), трубка струму (в).

Описуючи потік рідини, часто використовують терміни - поле швидкостей і профіль швидкостей, що являють собою відповідно значення швидкостей у всіх точках простору і точках перерізу трубки струму у фіксований момент часу. Якщо лінії струму і поле швидкостей не змінюються з часом, то рух рідини зветься стаціонарним. При стаціонарному плині траєкторії частинок залишаються незмінними. Швидкість частинки може змінюватися при її русі вздовж лінії струму, але у кожній точці лінії струму вона зберігається за величиною і напрямком. Якщо поле швидкостей і лінії струму змінюються з часом, то такий плин зветься нестаціонарним. У цьому випадку лінії струму під час плину зникають і знову з'являються, у деяких випадках за формою вони нагадують вихори (мал. 1.136), такий плин рідини зветься турбулентним або вихровим.

Рівняння нерозривності струменя. Розглянемо стаціонарний плин рідини. Позначимо через и середню швидкість плину рідини для довільно вибраного перерізу S трубки струму. Маса рідини, що протікає через цей переріз за одиницю часу, залишається постійною через те, що рідина не розривається і не стискається в звичайних умовах, тобто

dm/dt = const. (1.15)

(Якщо б ця умова не виконувалася, то тубка струму не зберігалася б постійною у просторі). Оскільки dm = Sdl = = S*υ*dt, з рівняння (1.15) отримаємо:

p*S*υ= const. (1.16)

Для нестисливої рідини (ρ = const) рівняння нерозривності струменю дає зв'язок між площиною перерізу трубки струменю і середньою швидкістю плину рідини:

S*υ - const, або для різних перерізів трубки струму (див. мал. 1.14)

S₁-υ₁=S₂-υ₂. (1.17)

Величина Q = dV/dt = S*υ [м³/с], що дорівнює об'єму рідини, який протікає через переріз трубки струму за одиницю часу, зветься об'ємною швидкістю плину рідини. При стаціонарному плині вона залишається величиною сталою. Аналогами цієї величини у фізіології є витрата крові або хвилинний об'єм крові (ХОК). Виходячи з визначення об'ємної швидкості плину рідини, хвилинний об'єм крові можна обчислити як відношення ударного об'єму крові V_y_ддо періоду скорочення серця Т, або добуток V_y_дначастоту серцевих скорочень ЧСС -1/Т:

XOK=V_y_д/T=V_y_д*ЧCC.

Коли кров рухається по еластичних судинах, внаслідок їх деформації при зміні тиску лінії струму не залишаються постійними. У цьому випадку рівняння нерозривності струменю може бути подано таким чином:

dV/dt = Q₁(t) - Q₂(t), або 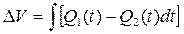, (1.18)

де Q₁(t) та Q₂(t) - відповідно приплив та відток крові для ділянки судини. Ці рівняння будуть в подальшому використані при вивченні фізичних основ реографи.

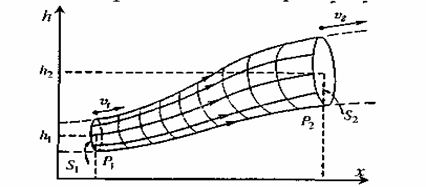
Мал. 1.14. Трубка струму.

Рівняння Бернуллі. Розглянемо стаціонарний плин ідеальної рідини. Виділимо у просторі трубку струму (мал. 1.14) і розглянемо енергію малого елемента об'єму рідини з масою Δm = ρΔV, що протікає через переріз трубки струму за деякий час. Оскільки рідина є ідеальною і робота сил тертя дорівнює нулю, то повна енергія деякого елементу об'єму рідини у цьому випадку буде залишатися величиною сталою при русі вздовж трубки струму:

Е = Е_к+ Е_п + Е_ст = const, (1.19)

де Е_к = Δm*υ²/2 - кінетична енергія, Е_п = Δmgh - потенціальна енергія, а Е_ст = P-ΔV - потенціальна енергія виділеного об'єму рідини. Підставляючи ці вирази у формулу (1.19) і вводячи об'ємну густину енергії w = E/ΔV, отримаємо рівняння Бернуллі, котре являє собою закон збереження енергії для одиниці об'єму рідини, що рухається

w = 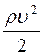+ pgh + P = const. (1.20)

Таким чином, фізичний зміст рівняння Бернуллі полягає в тому, що об'ємна густина енергії w ідеальної рідини при її стаціонарному плині залишається величиною сталою. Зауважимо, що розмірність об'ємної густини енергії дорівнює [w] = [E]/[ΔV] - Дж/м³- Н/м², тобто вона збігається з розмірністю тиску [ρ] = Па = Н/м². Тому в гідравліці компоненти об'ємної густини енергії w називають: ρυ²/2 - динамічним, ρgh - гідростатичним та Р - статичним тисками. У цьому випадку рівняння Бернуллі свідчить про те, що сумарний тиск залишається постійним вздовж трубки струму при стаціонарному плині ідеальної рідини.

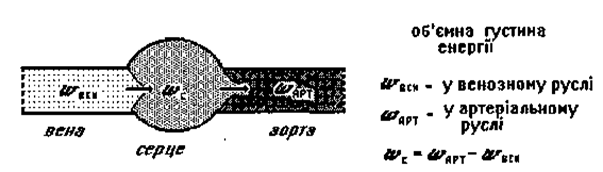
Мал. 1.15. Об'ємна енергія крові: w_вен-yвенозному руслі; w_арт -y артеріальному руслі; їх різниця w_c= w_арт- w_вен .

Коли кров рухається по судинному руслу, величина об'ємної густини енергії різко змінюється при переході з венозного русла до артеріального (мал. 1.15). Ця зміна обумовлена діяльністю серця як насоса. Насосна функція серця полягає у зміні об'ємної густини енергії крові. Насосну функцію серця можна характеризувати різницею об'ємних густин енергії на вході та виході серця, тобто величиною

w_c= w_арт- w_вен .

Розрахунок цих величин за формулою (1.20) свідчить про те, що більш як 95% від величини w_c припадає на потенціальну енергію стисненої рідини в аорті, яка, в свою чергу, визначається величиною середнього артеріального тиску. Отже, величина артеріального тиску дозволяє судити про насосну функцію серця й енергію крові на виході серця, за рахунок якої відбувається її подальший рух по судинному руслу. Зауважимо, що у всіх теплокровних середнє значення артеріального тиску одне і те ж, порядку 90-100ммHg, у той час, як інші найважливіші показники системи кровообігу (такі, як хвилинний об'єм, частота серцевих скорочень) значно відрізняються. Більш того, в організмі існує спеціальна система слідкування за артеріальним тиском, а точніше - за об'ємною густиною енергії крові. Саме її підтримка на певному рівні дозволяє забезпечити рух крові крізь капіляри з оптимальною швидкістю, при якій відбувається рівномірна віддача кисню оточуючим тканинам (незалежно від того, яка їх кількість включена до роботи і який хвилинний об'єм протікає крізь них).

З наведеного вище можна зробити висновок, що кількість енергії, що її передає серце одиниці об'єму крові, є однією з найважливіших констант організму. Спеціальні регуляторні механізми серця забезпечують саме такий режим скорочення міокарда, за якого при різних навантаженнях серце було б здатне підтримувати на певному рівні об'ємну густину енергії потоку крові, витрачаючи при цьому мінімум хімічної енергії при скороченні міокарда.

Рівняння руху і рівноваги рідини. Виділимо у рідині елементарний об'єм ΔV циліндричної форми з перерізом S і довжиною Δх (мал. 1.16). За другим законом Ньютона:

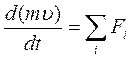
або для об'ємних сил:

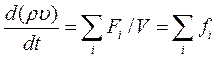(1.21)

Розглянемо сили, що діють на елемент об'єму рідини. Результуюча сила тиску дорівнює

F = S[P(x) - Р(х + dx)] = -SdP,

тоді як об'ємна сила тиску (сила, що діє на одиницю об'єму) є

.

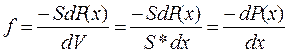Проводячи аналогічний розгляд для у, z-компонент сил, отримаємо:

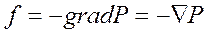, (1.22)

де 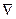- символ градієнта (так званий "оператор набла"). З рівняння (1.22) випливає, що об'ємна результуюча сила тиску за модулем дорівнює градієнту тиску.

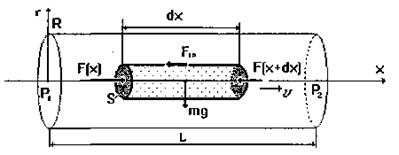
Мал. 1.16. Сили, що діють на елемент об'єму рідини.

Рівняння руху рідини (1.4) з урахуванням інших об'ємних сил, а саме, сили тертя f_mp, сили тяжіння ρg, інших зовнішніх сил f_зовн можна записати у вигляді:

ρ*dv/dt = -VP +f_mp + pg + f_зовн. (1.23)

Якщо сила тиску врівноважується іншими силами за умови, що dv/dl = 0, то

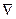P+f_mp+ρg+ f_зовн = 0. (1.24)

Аналогічним рівнянням описують і рівноважний стан рідини, коли рідина знаходиться у спокої, тобто швидкість υ = 0.

Плин ньютонівської рідини по горизонтальній трубці

Формула Пуазейля. Плин в'язких рідин по циліндричних трубках має для медицини особливий інтерес. Судинна система може бути представлена сіткою циліндричних трубок різного діаметра, лінійна й об'ємна швидкості плину рідини по яких залежить не лише від властивостей рідини, а й від геометричних розмірів судин. Визначимо лінійну й об'ємну швидкості плину для стаціонарного потоку в'язкої

рідини крізь судину радіусом R, довжиною L, з перепадом тиску на його кінцях Р₁-Р₂ (мал. 1.16).

Запишемо рівняння руху (1.24) для стаціонарного плину ньютонівської рідини, коли зовнішні сили дорівнюють нулеві, і сила тяжіння не впливає на плин рідини:

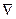-P+f_mp = 0 або P = f_mp. (1.25)

Припустимо, що градієнт тиску вздовж трубки струму є постійна величина: 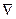P=(Р₂- Р₁)/L. Об'ємна сила тертя f_mp дорівнює (1.8):

,

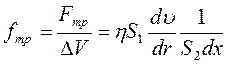де S₁ = 2πrdx – площа бічної поверхні циліндра, S₂ = πr² – площа перерізу циліндра радіуса г. Підставивши ці вирази у рівняння (1.25), отримаємо диференційне рівняння, що визначає зміну швидкості рідини вздовж радіуса трубки:

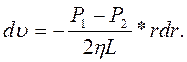
Проінтегруємо це рівняння

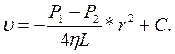
де сталу інтегрування С знаходимо з умови υ = 0 на границі судини, тобто при r = R. Це дає 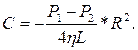. В результаті тримуємо формулу Пуазейля, яка визначає профіль швидкості ньютонівської рідини в циліндричній трубці

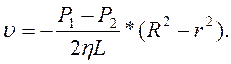
(1.26)

З цієї формули випливає, що профіль швидкостей ньютонівської рідини в циліндричній трубці описується параболічним законом (мал. 1.17а).

Формула Пуазейля дозволяє визначити об'ємну швидкість плину ньютонівської рідини. Виділимо у перерізі трубки шар рідини товщиною dr і площею dS = 2πrdr (мал. 1.17б). Об'єм рідини, що протікає крізь цю площу за одиницю часу, дорівнює

dQ = v(r)dS = v(r)-2πrdr.

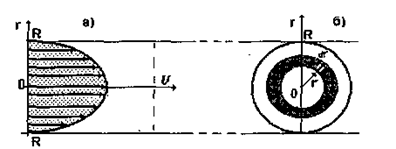
Мал. 1.17. Характеристики плину ньютонівської рідини по циліндричній трубці: а) профіль швидкостей; б) переріз трубки

струму.

Підставивши в цю формулу вираз (1.26) для швидкості і інтегруючи отримане рівняння, дістанемо формулу, що дозволяє визначити об'ємну швидкість рідини:

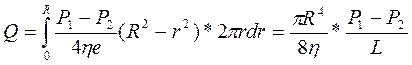. (1.27)

Помноживши об'ємну швидкість рідини на час плину, отримаємо формулу для визначення об'єму рідини V, що протікає через переріз судини за час t:

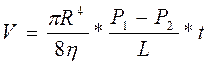(1.28)

З формул (1.27) та (1.28), які звуться формулами Гагена-Пуазейля, випливає, що кількість рідини, яка протікає крізь судину, найбільш суттєво залежить від його радіуса і зменшується із зростанням в'язкості рідини.

Формула (1.27), що зв'язує між собою об'ємну швидкість рідини і різницю тисків на кінцях судини, має вигляд, аналогічний закону Ома:

Q= (P₁-P₂)/W, (1.29)

тому величину W = 8ηL/(πR⁴) називають гідравлічним опором.

Графічні зображення зв'язку Q-ΔР називають діаграмами "витрата-тиск". їх вигляд для ньютонівської рідини і рідини, в'язкість якої залежить від градієнта швидкості (наприклад, для крові), подані на мал. 1.18.

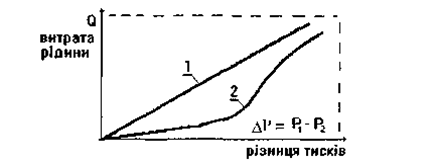
Мал. 1.18. Діаграми ''витрата-тиск" для ньютонівської (1) та неньютонівської (2) рідин.

1.2.5. Критерії механічної подібності рідин, що рухаються

Незважаючи на різноманітність руху рідин у природі, можна поставити питання: яким умовам повинні відповідати параметри потоку і параметри рідин (густина, в'язкість тощо), щоб рухи рідин були механічно подібні? Якщо подібність має місце, то, знаючи картину плину рідини в одній системі, можна передбачити і характер плину рідини в іншій, геометричне подібній системі. Це має важливе значення не лише у техніці (випробування моделей літаків, кораблів тощо), айв експериментальній медицині (наприклад, при дослідженні процесів обтікання кров'ю різних моделей серцевих клапанів, особливостей плину рідин по штучних судинах, криволінійному ложеві насоса апарату штучного кровообігу тощо).

Розглядаючи будь-який плин рідин і рівняння його руху, можна виділити деякі важливі параметри рідини (η -в'язкість, ρ — густина, χ -модуль об'ємної пружності) і характеристики її руху (υ - швидкість, L - характерні розміри, τ - деякий характерний час, протягом якого відбуваються помітні зміни плину тощо). У гідродинаміці відомі декілька безрозмірних величин, що являють собою комбінацію цих параметрів. Це числа Рейнольдса (Re), Фруда (F), Маха (М), Струхаля (S). Кожне з цих чисел має певний фізичний зміст. Так, число Маха є відношенням швидкостей руху тіла і звука у даному середовищі (М= υ/c). Число Струхаля - відношення деякого характерного розміру потоку рідини і розмірів тіла (S = υ*τ/L). Число Фруда (Ф = υ²lgL) визначає відношення кінетичної енергії рідин до її приросту, обумовленого роботою сили тяжіння на деякій характерній відстані (чим більше число Фруда, тим більша роль інерції у порівнянні з дією сили тяжіння).

Одним з найважливіших критеріїв подібності є число Рейнольдса. За порядком величини воно дорівнює відношенню кінетичної енергії рідини до витрати її, обумовленої роботою сил в'язкого тертя на характерній довжині. Дійсно, кінетична енергія рідини Е_к ~ ρL³υ², робота сил в'язкості А = = F_m*L. Силу в'язкого тертя знайдемо за

формулою Ньютона F_m ~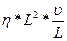. Відношення кінетичної енергії Е_к до роботи А і становить число Рейнольдса:

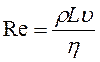(1.30)

Число Рейнольдса, таким чином, визначає відносну роль інерції і в'язкості рідини при її плині. При великих числах Рейнольдса головну роль відіграє інерція, при малих - в'язкість. При плині рідини по циліндричних трубках у ролі характерного розміру L часто використовують радіус чи діаметр судини. Потоки рідин вважаються подібними, якщо для них числа Рейнольдса і Фруда збігаються. При малих числах Рейнольдса плин в'язких рідин є ламінарним, при зростанні швидкості ламінарний плин стає нестійким і перетворюється в турбулентний. Турбулентний плин - це такий плин, гідродинамічні характеристики якого (швидкість, тиск) різко та нерегулярно змінюються з часом і у просторі. Частинки рідини рухаються по складних траєкторіях, рідина інтенсивно перемішується. Прикладом такого

руху є рух крові при її вигнанні з шлуночків серця, її плині по аорті тощо.

Слід зауважити, що при турбулентному русі рідини не діють звичайні формули гідродинаміки (гемодинаміки). Так, на відміну від закону Гагена-Пуазейля і формули Пуазейля, згідно з якими при ламінарному плині об'ємна швидкість Q чи лінійна швидкість v пропорційні різниці тисків υ ~ ~ Р₁-Р₂ У першому степені, при турбулентній течії рідини за певними умовами має місце закон Шезі, згідно з яким лінійна швидкість υ~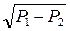. Для рідини, що тече по певній судині, можна визначити значення швидкості υ_к_p, при якій рух із ламінарного перетворюється у турбулентний. Число Рейнольдса, при якому відбувається це явище, зветься критичним:

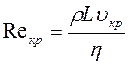. (1.31)

У геометричне подібних системах перехід від ламінарного до турбулентного плину відбувається завжди при одних і тих самих значеннях числа Рейнольдса. Так, згідно (1.31) критичне значення числа Re для в'язкої рідини, що тече по довгій циліндричній трубці, становить 2300. Значення чисел Рейнольдса для крові в різних ділянках судинного русла подані у табл. 1.2.

Зауважимо, що зміна величини в'язкості крові (наприклад, при анемії) може діагностуватися завдяки виникненню турбулентних шумів. Це пояснюється тим фактом, що при анемії коефіцієнт в'язкості зменшується у 2-3 і більше разів. Відповідно число Рейнольдса збільшується, оскільки Re ~ 1/η\. Як наслідок, число Рейнольдса стає більшим за своє критичне значення і виникає перехід від ламінарного плину крові до турбулентного.

Ще одне медичне застосування переходу між ламінарною і турбулентною течією крові пов'язане з вимірюванням кров'яного тиску методом Короткова. У цьому методі систолічний (верхній) тиск вимірюється у момент, коли кров починає протискуватися через отвір в артерії, стиснутій за допомогою манжети. Саме у цей момент виникають шуми, обумовлені появою турбулентної течії крові. Діастолічний (нижній) тиск фіксується у момент, коли ці шуми зникають внаслідок послаблення манжети і переходу течії від ламінарної до турбулентної.

1.2.6. Пульсові хвилі

Існування пульсових хвиль легко виявити. Для цього достатньо притиснути пальцем променеву або сонну артерії і відчути "биття" стінки артеріальної судини. Чутливі пристрої можуть зареєструвати коливання стінок і венозних судин, які значно слабкіші за коливання артеріальних судин. Як виникають пульсові коливання, у чому полягає їх фізична природа? Проблема ця досить складна і вирішена лише частково. Плин крові по судинному руслу супроводжується різноманітними коливаннями: це і поздовжні хвилі тиску, що поширюються у рідкому середовищі зі швидкістю звуку, це і періодичні зміни швидкості руху рідини, пов'язані з переривчастим викидом крові серцем в судинне русло, це і періодична зміна просвіту судини при зміні його кровонаповнення. Всі ці процеси взаємопов'язані, вони характеризують єдине явище - рух крові по складному дереву судинного русла.

Розглянемо спрощену модель виникнення пульсових хвиль в еластичній судині. Зрозуміло, що їх походження пов'язане з діяльністю серця. Коли б на виході серця плин крові був сталим, то ніяких пульсацій не виникало б. З іншого боку, коли б стінки судин були дуже жорсткими, то навіть при пульсуючому кровотоці рух стінок був би практично непомітним. Отже, походження пульсових хвиль пов'язане з реакцією пружних стінок судини на пульсуючий плин крові, що виникає при періодичній роботі серця.

Виділимо невелику ділянку еластичної судини (мал. 1.19), на одному з кінців якого знаходиться поршень. На

поршень короткочасно діє сила F. Рідина біля поршня внаслідок її інерції не встигає переміститися вздовж судини, дія сили викликає зростання тиску на стінки -ділянка розширюється доти, доки напруження стінки не компенсує зростання тиску всередині судини. Оскільки натяг стінки у цій області буде більшим, ніж у сусідніх, рідина буде переміщуватися далі по судині. Переміщення рідини приведе до зменшення тиску на цій ділянці, судина почне відновлювати первісний об'єм у той час, як об'єм сусідньої ділянки буде зростати. Процес повторюється після нового поштовху поршня. По еластичній стінці буде поширюватися пульсова хвиля.

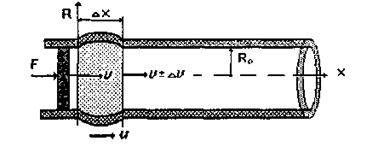
Мал. 1.19. Модель ділянки еластичної судини.

Запишемо рівняння пульсової хвилі. Для цього розглянемо рух ідеальної рідини по еластичній трубці під дією одних лише сил тиску. Виділимо ділянку завдовжки Ах і об'ємом V. Позначимо зміну радіуса ділянки трубки при розширенні через £, тоді поточне значення радіуса дорівнюватиме

R(x,t) = R₀ + e(x,t). (1.32)

Рівняння пульсової хвилі, яке характеризує процес розповсюдження зміни радіуса судини є вздовж її осі, має такий вигляд:

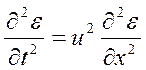, (1.33)

де и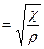— - швидкість поширення пульсової хвилі.

За умови відсутності поздовжнього натягу (так, що трубка буде скорочуватись при розширенні) модуль об'ємної пружності χ для тонкої циліндричної судини радіусом R і товщиною стінки h визначається за формулою (1.7) без множника 1 - μ². Після підстановки маємо формулу Моєнса-Кортевега для швидкості:

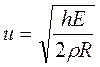(1.34)

Таким чином, швидкість поширення пульсової хвилі залежить як від геометричних параметрів судини (радіуса і товщини), так і від пружних властивостей судинної стінки.

Коефіцієнт Пуассона для судини є величина постійна і дорівнює приблизно 0.5. Модуль Юнга, як було показано вище, не залишається величиною сталою для судини, тому швидкість поширення пульсових хвиль може значно змінюватися. Деякі приклади зміни швидкостей розповсюдження пульсових хвиль наведено на мал. 1.20. Швидкість пульсової хвилі значно змінюється при різних судинних захворюваннях, у зв'язку з цим її клінічне визначення дозволяє одержати додаткову інформацію для оцінки функціонального стану стінок судин.

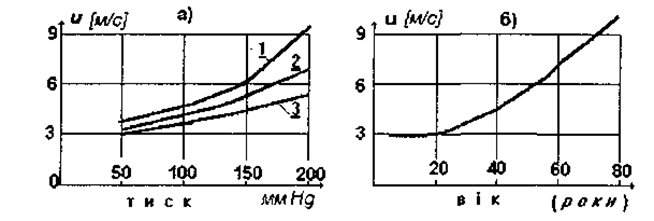
Мал. 1.20. а) зміна швидкості з ростом тиску (1, 2, 3 - відповідно для похилого, середнього та молодого віку), б) зміна швидкості з

віком.

Рух крові по серцево-судинній системі досить складне явище. Складну будову має кровоносне русло, що являє собою розгалужену систему еластичних судин різного типу. Сама рідина - кров - є складна суспензія, реологічні характ

<2 3 456 7 8 >

Дата добавления: 2020-11-18; просмотров: 966;