Расчет емкости СПС с коммутацией каналов
При проектировании сетей сотовой мобильной связи необходимо оцени
вать трафик (интенсивность нагрузки) системы связи, позволяющей, в свою
очередь, оценить число обслуживаемых абонентов в соте и во всей сети в целом.
Основными величинами, необходимыми для построения математических моделей трафика, являются:
- средняя частота поступления вызовов ‹λ›, измеряемая числом вызовов в единицу времени ([λ] = вызов/ч, вызов/с); поток вызовов достаточно полно можно характеризовать средней частотой поступления вызовов (интенсивностью поступления вызовов) λ;
- средняя продолжительность обслуживания одного вызова (средняя продолжительность одного разговора) ‹Т›, измеряемая в единицах времени;
- средняя интенсивность нагрузки (интенсивность трафика), равная произведению А = ‹λ›·‹Т›, измеряемая в эрлангах (Эрл).
Поступление вызовов, как и продолжительность обслуживания T(t), являются случайными величинами, зависящими от времени. Соотношения между предполагаемой нагрузкой, числом каналов и показателем качества обслуживания описываются вероятностными характеристиками.
Вероятность поступления вызовов описывается распределением Пуассона, определяющим вероятность поступления k-вызовов (дискретная случайная величина) за время t:
 |
при [‹λ›t] >0, k ≥ 0. При этом среднее число вызовов на интервале времени t:
 |
а дисперсия числа вызовов на том же интервале:
где ‹λ› - средняя частота поступления вызовов.
Продолжительность обслуживания одного вызова (длительность занятости канала связи) является непрерывной случайной величиной τ(t), плотность распределения вероятностей которой описывается экспоненциальным законом распределения:
 |
которому соответствует среднее значение (математическое ожидание) и дисперсия: τ = ‹Т›, ∆τ =‹Т›2, то есть среднее значение совпадает со средней продолжительностью обслуживания одного вызова ‹Т›.
В математических моделях трафика выполняются следующие условия:
- поток вызовов подчиняется распределению Пуассона;
- продолжительность обслуживания вызовов подчиняется экспоненциальному распределению, при этом различные модели отличаются одна от другой тем, какая участь постигает вызовы, поступающие в моменты времени, когда все каналы системы заняты. Эти вызовы могут аннулироваться (модель системы с отказами), либо становиться в очередь и ждать освобождения канала неопределенно долгое время, после чего обслуживаться в течение необходимого интервала времени (модель системы с ожиданием (очередями));
- возможны промежуточные случаи, например, модели с ожиданием, нов течение ограниченных временных интервалов времени.
При расчетах емкости систем сотовой мобильной связи обычно используется модель системы с отказами(lost-calls-cleared conditions – условия сброса вызовов, получивших отказ), называемая моделью Эрланга В. В данной модели вероятность отказа (то есть вероятность поступления вызовов в момент, когда все каналы заняты) определяется выражением:
 |
где N – число каналов;
А = ‹λ›·‹Т› - трафик.
Вероятность того, что все каналы свободны, для данной модели определяется выражением:
Вероятность того, что занято «к» каналов, определяется выражением:
 |
 |
Среднее число занятых каналов:
 |
При вероятности отказа РВ > 0,1 сравнительно небольшое возрастание трафика (А > 40) приводит к резкому росту вероятности отказа, то есть к резкому ухудшению качества обслуживания. Поэтому расчет емкости системы сотовой мобильной связи проводится для значений РВ в пределах от 0, 01 до 0,05.
На практике обычно пользуются табличным представлением вероятности блокирования вызова в системе с отказами (модель Эрланга В) – таблица 3.1.
Таблица 3.1.
| Число каналов N | Вероятность отказа РВ = ψ(А,N) | ||||
| 0,002 | 0,01 | 0,02 | 0,05 | 0,1 | |
| А – трафик (эрланг) | |||||
| 0,002 | 0,01 | 0,02 | 0,05 | 0,11 | |
| 0,07 | 0,15 | 0,22 | 0,38 | 0,6 | |
| 0,9 | 1,36 | 1,66 | 2,22 | 2,88 | |
| 3,4 | 4,5 | 5,1 | 6,2 | 7,5 | |
| 10,1 | 12,0 | 13,2 | 15,2 | 17,6 | |
| 17,6 | 20,3 | 21,9 | 24,8 | 28,11 | |
| 25,6 | 29,0 | 31,0 | 34,6 | 38,8 | |
| 33,9 | 37,9 | 40,3 | 44,5 | 49,6 | |
| 77,5 | 84,1 | 88,0 | 95,2 | 104,1 | |
| 122,9 | 131,6 | 136,8 | 146,7 | 159,1 | |
| 169,2 | 179,7 | 186,2 | 198,5 | 214,3 |
После определения величины трафика А из таблицы 3.1 (после проведения оценки числа вызовов абонентов сотовой сети в среднем в час ‹λl›, а также средней продолжительности разговора ‹Тl›), рассчитывается число абонентов в одной соте:
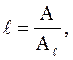
где Аl – трафик для одного абонента (Аl = ‹λl›·‹Тl›).
Число абонентов в «m» сотах:
 |
Дата добавления: 2020-10-25; просмотров: 620;











