Лабораторный практикум

Лабораторная работа № 1

Определение периода колебания маятника

Задание 1

На длинной нити подвешивается магнит, а в качестве датчика магнитного поля используется геркон (герметичный контакт). Для проведения компьютерного эксперимента геркон подключается к контактам 15 (D3) и 25 (GND). Геркон устанавливается в точке покоя маятника. Под действием магнитного поля ферромагнитные пластинки геркона соединяются, замыкая цепь.

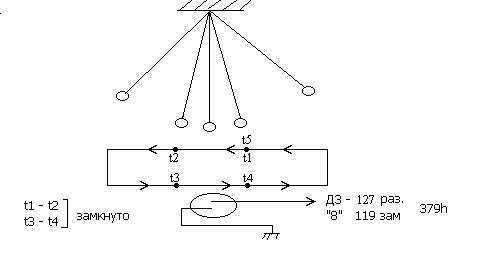
Отклоним магнит в крайнее правое положение, запустим программу и отпустим маятник. В момент замыкания геркона программа выходит из цикла строк 20-30 и фиксирует в t1 начало периода колебания. В момент времени t2 фиксируется размыкание геркона после прохождения магнита. В момент t3 магнит возвращается и вновь замыкает геркон и в t4 фиксирует его размыкание. Отклоняясь вправо и возвращаясь в исходную точку, фиксируется вновь время t5. Период колебания маятника Т = t5 – t1

10 cls очистка экрана

20 a=inp ( &h 379) чтение состояния порта

30 if =127 then go to 20 проверка замкнутого состояния геркона

40 t1=timer запись времени начала падения (точность 0,05 с)

50 a= inp ( &h 379)

60 if a=119 then go to 50 проверка замкнутого состояния геркона

70 t2= timer

80 a= inp ( &h 379)

90 if a =127 then go to 80

100 t3= timer

110 a= inp ( &h 379)

120 if a= =119 then go to 110

130 t4= timer

140 a= inp ( &h 379)

150 if a =127 then go to 140

160 t5= timer

170 t= t5 – t1

180 print t

185 sleep 1

190 goto 20

Задание № 2

Построить на экране монитора график зависимости периода колебания маятника от времени Т=F(t).

Лабораторная работа № 2

Определение ускорения свободного падения

Задание № 1

Измерение ускорения свободного падения производится по определению времени падения стального шарика с высоты 2 метра. При точности системных часов компьютера 0,05 сек. ошибка измерения ускорения свободного падения составляет 7-10 %. Схема лабораторной установки показана на рис 5.

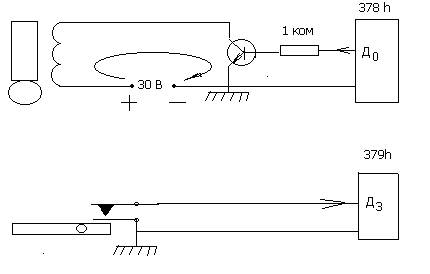
рис 5

Программа, при ее запуске, удерживает стальной шарик поднесенный к соленоиду в течении 5 секунд. Время падения тела определяется как t2–t1 внутренним таймером компьютера и далее вычисляется ускорение свободного падения

10 out &h378,1 магнит удерживает стальной шарик

20 sleep5 удержание шарика 5 сек.

30 out &h 378,0 начало падения шарика

40 t1= timer t1 начальный момент падения

50 а= inp ( &h 379) опрос контакта на размыкание

60 if a=127 then go to 50

70 t2= timer t2 момент касания нижней платформы

80 print 2/ (t2 – t1) * (t2 – t1) печать величины ускорения

Задание № 2

Более точные результаты можно получить если использовать эталонный генератор частотой 10 КГц, и несколько изменить схему на Рис.5 подключенный к биту D3 порта 379h. В новой постановке, после начала падения стального шара, компьютер будет считать количество импульсов эталонного генератора до касания шара рычага и замыкания контакта К1.

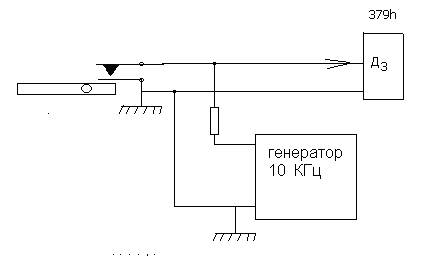
Программа эксперимента в этом случае имеет следующий вид:

10 out &h378,1 магнит удерживает стальной шарик

20 sleep5 удержание шарика 5 сек.

30 out &h 378,0 начало падения шарика

40 а= inp ( &h 379) опрос контакта на размыкание

50 if a=127 then goto 40

60 a=inp (&h 379)

70 if a=119 then goto 60

80 n= n +1 счет импульсов

90 t2=timer

100 t=t2-t1

110 if t>3 then goto 130

120 goto 30

130 print n

Задание 3

В предыдущем эксперименте необходим генератор на 10 КГц. Можно в программе организовать циклы и в относительных единицах определить время падения шара.

10 out &h378,1 магнит удерживает стальной шарик

20 sleep5 удержание шарика 5 сек.

30 out &h 378,0 начало падения шарика

35 for n=0 to 200000

40 а= inp ( &h 379) опрос контакта на размыкание

50 if a=119 then goto 60

55 next n

60 print n

Затем с помощью отдельной программы, определим время выполнения этого цикла и абсолютное время падения шара.

t1 = timer

for n=0 to 200000

next

t2= timer

t=t2-t1

print t