Пересечение гранных поверхностей
При пересечении двух многогранников общим геометрическим элементом является замкнутая ломаная линия, состоящая из участков прямой, так как многогранники образованы из плоскостей, а линия пересечения плоскостей представляет собой прямую. Точки излома получаются в местах пересечения граней одного многогранника с ребрами другого.
В том случае, когда один из многогранников занимает частное положение (т.е. его боковые грани проецируются на одну из плоскостей проекций в многоугольник), задача построения линии их пересечения решается достаточно просто. Ввиду того, что одна из проекций многогранника – многоугольник, проекция линии пересечения на эту плоскость проекций совпадает с ним. Поскольку линия пересечения многогранников принадлежит каждому из них, то задача сводится к построению отсутствующих проекций ломаной линии, а следовательно, к построению проекций точек на поверхности многогранника и соединению из отрезками прямой. Заметим, что частное положение может занимать лишь призма, так как только ее можно расположить таким образом, чтобы боковые ребра, а значит, и грани были перпендикулярны плоскости проекций.
Рассмотрим описанные приемы построения на примере.
Пусть пересекаются пирамида и призма частного положения (рис. 6.1). Требуется построить проекции линии их пересечения.
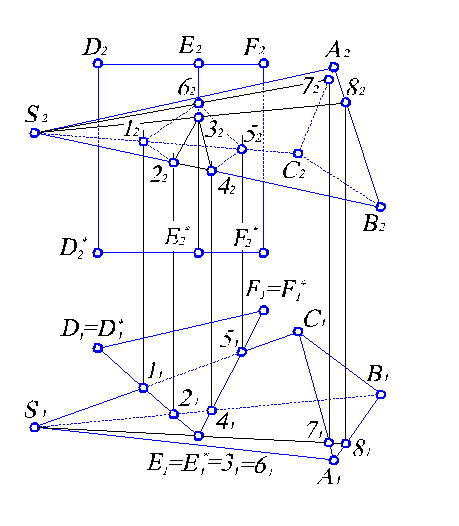
Рис. 6.1. Построение линии пересечения пирамиды и призмы частного положения.
Поскольку призма расположена так, что все ее боковые грани перпендикулярны П1, то на П1 ее боковая поверхность проецируется в линию, точнее в треугольник D1E1F1. И горизонтальной проекцией линии пересечения призмы DEFD*E*F* и пирамиды SABC является ломаная линия 11Е151. Таким образом, горизонтальная проекция линии пересечения призмы и пирамиды получена без каких бы то ни было дополнительных построений. Следует учитывать, что грани призмы пересекают не только грань SAC, но и грани SBC и SAB пирамиды, что очевидно из рассмотрения чертежа (рис. 5.10) на П1. Следовательно, можно отметить все точки излома линии пересечения 11Е151, расположенные на пересечении ее с ребрами пирамиды. А именно, точки 11, 21, 31, 41, 51, 61. Очевидно, что 31=61, так как ребро ЕЕ* призмы пересекает две грани SAB и SAС пирамиды.
Линия пересечения на каждой из проекций должна быть замкнутой. Причем ясно, что можно соединять отрезками прямой лишь точки, лежащие на одной и той же грани. Эти правила универсальны, и относятся к любой задаче о пересечении многогранников.
Тогда на П1 получаем горизонтальную проекцию линии пересечения призмы и пирамиды в виде ломаной 11213141516111, лежащей на гранях пирамиды (вместе с тем и призмы).
Для нахождения фронтальной проекции этой линии необходимо решить задачу построения проекций ломаной линии на поверхность пирамиды. Достаточно построить фронтальные проекции указанных точек. Так как точки 1, 2, 4, 5 лежат на ребрах пирамиды, то их фронтальные проекции 12, 22, 42, 52 легко получить по линиям связи. Для нахождения фронтальных проекций 32 и 62 точек 3 и 6, лежащих на гранях SAB и SAС соответственно, необходимо через точки 31 и 61 провести образующие S171 и S181. Точки 7 и 8 лежат на основании пирамиды, поэтому по линиям связи можно найти фронтальные проекции 72 и 82 на соответствующих ребрах основания А2С2 и А2В2 пирамиды. Построив фронтальные проекции S272 и S282 образующих, по линиям связи отметим на них точки 32 и 62. Соединив точки, получим замкнутую ломаную 12223242526212. Последовательность соединения определяется по горизонтальной проекции на основании правила принадлежности соседних точек пересечения одной и той же грани. Например, ошибочным было бы соединение точек 12 и 32, так как одна из них лежит на ребре S2С2, а другая на грани S2A2B2.
Видимость точек и линий на П2 определяется по принадлежности граням пирамиды, так как обе грани D2E2E2*D2* и Е2F2F2*E2* являются видимыми. Поскольку грани S2A2С2 и S2В2С2 невидимые, то и точки, и прямые, лежащие на них, также невидимые. Проведя невидимые линии пунктиром, получим решение в окончательном виде.
Рассмотрим случай, когда оба многогранника занимают общее положение в пространстве, решение задачи о нахождении линии их пересечения усложняется, поскольку нужно строить все проекции этой линии. Линия пересечения многогранников проходит через точки пересечения ребер первого многогранника с гранями второго и граней первого с ребрами второго.
Для решения применим метод секущих вспомогательных плоскостей. Чтобы получить какую-либо точку пересечения многогранников, необходимо найти линию пересечения вспомогательной плоскости с одним из них, затем с другим, далее – точку пересечения этих линий.
Рассмотрим пример.
Пусть пересекаются четырехгранная пирамида SABCD и трехгранная призма EFGE*F*G* (рис. 6.2). Необходимо определить проекции точек пересечения: ребер призмы с гранями пирамиды; ребер пирамиды с гранями призмы.
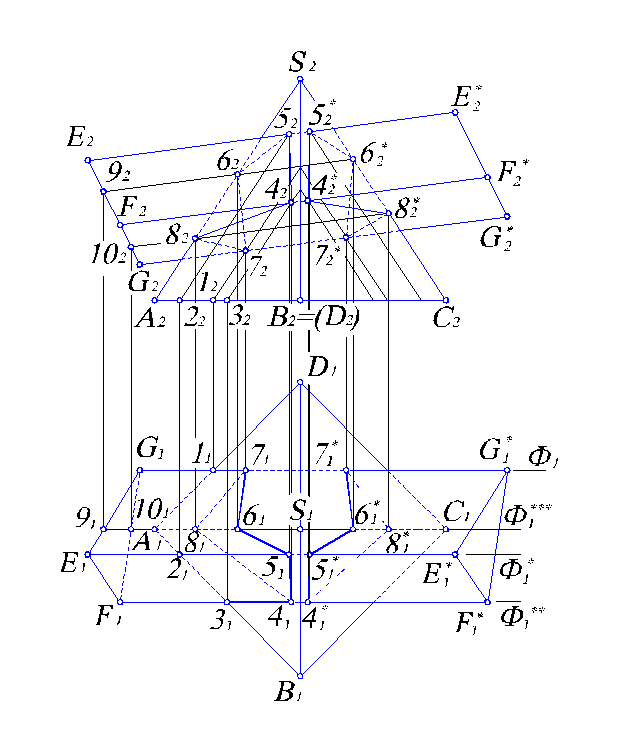
Рис. 6.2. Построения линии пересечения пирамиды и призмы общего положения.
Через ребра призмы ЕЕ*,FF*, GG* проведем вспомогательные фронтальные плоскости уровня Ф, Ф*,Ф**. При выборе положения вспомогательной секущей плоскости в каждом конкретном случае руководствуемся правилом: вспомогательная плоскость должна быть плоскостью частного положения и пересекать многогранники по линиям, проекции которых построить несложно. В данном случае линии пересечения с призмой плоскостей Ф, Ф*,Ф**, проходят по ее ребрам, значит, ее проекции совпадают с проекциями ребер призмы.
Рассмотрим одну из вспомогательных плоскостей Ф. Ее горизонтальная проекция Ф1 проходит по ребру G1G1*. Линия пересечения с пирамидой проходит через точку основания 11 и параллельна ребру S1А1. По линии связи находим фронтальную проекцию 12 и через нее проводим прямую, параллельную A2S2, которая является фронтальной проекцией линии пересечения плоскости Ф и пирамиды. Очевидно, что там, где эта линия пересекает ребра G2G2* и лежит фронтальная проекция 72 точки пересечения ребра GG* и грани пирамиды SAD. По линии связи найдем 71. Аналогично строятся точки 42, 52, а по ним 41, 51.
Проведем вспомогательную плоскость Ф*** теперь по ребру SA пирамиды. Тогда горизонтальная проекция линий пересечения плоскости Ф*** и граней EGG*E* и FGG*F* призмы проходит вдоль А1С1, через точки 91 и 101 соответственно основания призмы. По линиям связи найдем положение 92 и 102, через которые проведем образующие призмы, параллельные ее боковым ребрам. На пересечении с ребрами S2A2 получим точки 62 и 82. Далее по линиям связи – точки 61 и 81.
Соединив одноименные проекции точек, получим фронтальную 425262728242 и горизонтальную 415161718141 проекции замкнутой ломаной линии пересечения призмы и пирамиды. Видимость отдельных участков определяется по принципу (уже нашедшему применение в предыдущей задаче) – отрезок линии пересечения многогранников является видимым в проекции на какую-либо плоскость, если обе грани, на которых он лежит, видимые. В связи с этим невидимые участки изображены, как показано на рис. 6.1.
Для упрощения чертежа точки линии пересечения на правой стороне пирамиды (на гранях SBC и SDC) не обозначены, так как их построение ничем не отличается от рассмотренного выше.
Дата добавления: 2016-07-27; просмотров: 3030;











