Понятие коалиционных игр.
Ситуация значительно усложняется, когда в игре принимают участие более двух игроков. Водится понятие коалицииигроков, которые пользуются согласованной стратегией против интересов игроков, не входящих в их коалицию. Тогда могут быть вычислены ожидаемые выигрыши (значения игры) для каждой коалиции. В частности, вычисляются значения игры для каждого игрока в предположении, что он играет против коалиции всех других игроков. Обозначим эти значения g1,g2,…,gn. Нормальный выигрыш игрока должен быть не меньше соответствующего значения игры, назовем такой выигрыш обязательством. Таким образом, (s1,s2,…,sn) – обязательство, если si≥gi для i=1,2,…,n и ∑isi=G, где G – значение игры (суммарный выигрыш всех игроков, не обязательно равный нулю). Тогда решением для игры n лиц будет такое множество обязательств, что ни одно обязательство этого множества не доминирует над другими обязательствами того же множества и для любого обязательства, не принадлежащего этому множеству, найдется обязательство нашего множества, доминирующее над ним. (Теорема фон Неймана и Моргенштейна). Отношение доминирования используется только для двух игроков или больше и заключается в превышении выигрышей этих игроков в одном обязательстве по отношению к выигрышам этих же игроков в другом обязательстве.
В заключение приведем оценку теории игр, данную Вильямсом: «…хотя в настоящее время уже выяснены, несмотря на множество ограничений теории, многие ее специфические приложения, ее наибольший, пока неявный, вклад состоит в том, что она дает людям, имеющим дело со сверхсложными проблемами, самую общую ориентацию. Даже если эти проблемы не подаются строгому решению, она дает основу для работы над ними. Идея стратегии, различия между игроками, роль случайных событий, понятие матрицы выигрышей, идеи чистой и смешанной стратегии и т.д. дают драгоценную ориентацию лицам, которым необходимо обдумывать сложные конфликтные ситуации».
Практический блок
Примеры
Пример 1. ЗАО «ПК Элина» продает свой товар в основном бюджетным организациям. Объём продаж зависит от финансирования организаций. Распределение объемов продаж различного вида товара от степени финансирования представлено в таблице 2.7.10.
Таблица 2.7.10 – Распределение объёмов продаж от степени финансирования
| Наименование товара | Финансирование | Прибыль, руб./шт. | Затраты на хранение, руб./шт. | |
| «Хорошее» | «Плохое» | |||
| «Южный Урал» | ||||
| «Патриот» | ||||
| «Смерч-100» | ||||
| «Смерч-200» |
Необходимо определить оптимальный объем производства каждого вида товара, обеспечивающий максимальную прибыль.
Решение: Для решения задачи воспользуемся теорией игр.
На основании исходных данных строим платежную матрицу, где 1-я стратегия: объем производства, рассчитанный на хорошее финансирование, 2-я стратегия: объём производства, рассчитанный на плохое финансирование.
Таблица 2.7.11 – Платежная матрица
| «хорошее» | «плохое» | |
| 1-я стратегия | ||
| 2-я стратегия |
Элементы платежной матрицы вычисляются следующим образом:
а11 = 200 * 100 + 400 * 300 + 150 * 200 + 100 * 300 = 200000
а12 = 200 * 100 + 70 * 300 + 150 * 200 + 20*300 – 330*10 – 80*5= 73300
а21 = 200 * 100 + 70 * 300 + 150 * 200 + 20*300 – 200*10 – 50*5= 74750
а22 = 400 * 100 + 70 * 300 + 200 * 200 + 20 * 300 = 107000
Преобразуем платежную матрицу следующим образом:

|
|
74750 107000 1450 33700 1 23,24
Тогда система уравнений запишется в виде:


 87,38 х1 + х2 ≥ 1 х1 = 0,011
87,38 х1 + х2 ≥ 1 х1 = 0,011
х2 ≥ 1 х2 = 0,043
Целевая функция F* = х1 + х2 = 0,011 + 0,043 = 0,054
 Частота использования стратегий определяется как pi=xi *g=xi/F*, т.е для наших данных р1 = 0,011/0,054 = 0,2
Частота использования стратегий определяется как pi=xi *g=xi/F*, т.е для наших данных р1 = 0,011/0,054 = 0,2
р2 = 0,043/0,054 = 0,8
Произведем противоположные действия преобразованию платежной матрицы и получим минимальную прибыль (цену игры):
υ = (1/ F* ) * 1450 + 73300 = (1/0,054) * 1450 + 73300 = 100152 руб.
Теперь определим объём производства каждого вида товара:
«Южный Урал»: 200 * 0,2 + 400 * 0,8 = 360 штук,
«Патриот»: 400 * 0,2 + 70 * 0,8 = 136 штук,
«Смерч-100»: 150 * 0,2 + 200 * 0,8 = 190 штук,
«Смерч-200»: 100 * 0,2 + 20 * 0,8 = 36 штук.
Пример 2
Решить игру
 .
.
Чтобы гарантировать v > 0, прибавим ко всем элементам матрицы Н константу +1. Тогда получим матрицу
 .
.
Пара двойственных задач линейного программирования будет в данном случае выглядеть следующим образом:
Минимизировать
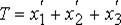
при условиях
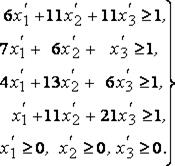
Максимизировать
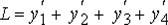
при условиях
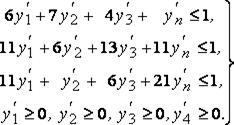
После применения симплексного метода получим оптимальное решение второй задачи:
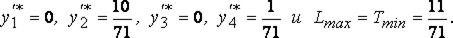
Отсюда
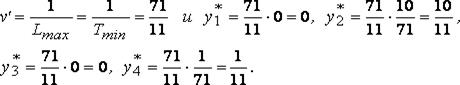
Таким образом, оптимальная стратегия игрока II есть
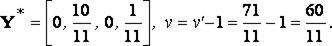
Оптимальное решение первой задачи:
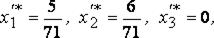
откуда
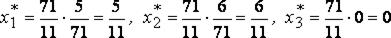
и
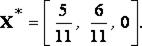
Итак,
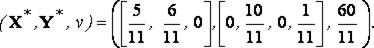
Пример 3
Пусть ежедневный спрос на булочки в магазине задается следующим распределением вероятностей:
| спрос | |||||
| Вероятность спроса | 0.20 | 0.25 | 0.30 | 0.15 | 0.10 |
Магазин закупает булочки по 2.5 руб. и продает по 4.9 руб. за штуку. Если булочка не продана в тот же день, то она реализовывается по 1.5 руб. Какое наибольшее число булочек необходимо заказывать ежедневно, если величина заказа может принимать одно из возможных значений спроса?
Прибыль от продажи «свежей» булочки составляет 4.9–2.5=2.4 руб.
Потеря от продажи «черствой» составляет 2.5–1.5=1 руб.
Представим модель данной задачи в виде игры магазина со спросом. Стратегия магазина – ежедневный объем заказа, при этом спрос может принимать одно из своих возможных значений. Составим платежную матрицу игры для магазина:
| Заказ магазина | Возможный ежедневный спрос | Ожид. прибыль | ||||
| 240-50 | ||||||
| 240-100 | 360-50 | 369.5 | ||||
| 240-150 | 360-100 | 480-50 | ||||
| 240-200 | 360-150 | 480-100 | 600-50 |
На пересечении строки с некоторым объемом заказа и столбца с возможным спросом находится элемент aij – ожидаемая прибыль магазина в этой ситуации. В последней колонке вычислена ожидаемая (средняя) прибыль в случае распределения вероятностей спроса в соответствии с условиями примера. Например, для третьей строки имеем 140*0.2+310*0.25+480*0.3+480*0.15+480*0.1=369.5. Кстати, выбор этой стратегии (ежедневный заказ – 200 булочек) и будет оптимальным, т.к. обеспечивает максимальную прибыль (правило Байеса).
Тесты
1. Платежной матрицей называется матрица, элементами которой являются:
а) годовые прибыли отраслевых предприятий;
б) выигрыши, соответствующие стратегиям игроков;
в) налоговые платежи предприятий.
2. Возможно ли привести матричную игру к задаче линейного программирования:
а) возможно;
б) невозможно;
в) возможно, если платежная матрица единичная.
3. Матричная игра –это:
а) игра двух лиц с несовпадающими интересами (неантагонистическая);
б) игра двух лиц с противоположными интересами;
в) игра многих (более двух) лиц.
4. Биматричная игра –это:
а) игра двух лиц с несовпадающими интересами;
б) игра двух лиц с противоположными интересами;
в) игра многих (более двух) лиц.
5. Чистые стратегии игры соответствуют:
а) однозначно принимаемым решениям;
б) решениям, принимаемым с определенной вероятностью;
в) произвольным решениям.
6. Смешанные стратегии игры соответствуют:
а) однозначно принимаемым решениям;
б) решениям, принимаемым с определенной вероятностью;
в) произвольным решениям.
7. Всегда ли матричная игра имеет решение?
а) да, в чистых стратегиях;
б) да, в смешанных стратегиях;
в) не всегда.
8. В чем заключается задача теории игр?
а) обеспечить минимальный средний выигрыш;
б) выявление оптимальных стратегий игроков;
в) выявление стратегий игроков;
г) содержание п.п.а-в;
д) содержимое п.п. а,б.
9. Какие классы состязательных задач Вы знаете?
а) когда с полной определенностью можно считать действия конкурента (выбор или метод, которым он пользуется при выборе своих действий) известными заранее;
б) выбор, сделанный конкурентом, не известен точно, но его можно предсказать с некоторой ошибкой. Следовательно, существует риск ошибиться, ибо выбор, произведенный конкурентами, точно не известен;
в) заранее ничего не известно о действительном или вероятном поведении конкурента. Такая ситуация возникает перед руководством промышленной фирмы при оценке реакции конкурентов в случае подготовки выпуска на рынок совершенно новой продукции;
г) заранее ничего не известно о действительном или вероятном поведении конкурента при составлении планов войны против предполагаемого противника, когда не известны ни место, ни время ее вспышки;
д) все вышеназванное.
10. Где эффективно используется теория состязаний?
а) в промышленности для разработки тактики торгов;
б) для разработки политики цен;
в) для разработки стратегии рекламы;
г) для выбора момента выпуска новых товаров на рынок;
д) все вышеназванное.
Ответы к тестам
| 1) б | 6) б |
| 2) а | 7) б |
| 3) б | 8) б |
| 4) а | 9) б |
| 5) а | 10) д |
Контрольные вопросы
1. Назовите виды игр и приведите их определения.
2. Как составляется платежная матрица?
3. Как определить верхнюю и нижнюю цену игры? Что такое седловая точка игры?
4. Что означает решение игры в смешанных стратегиях.
5. Каковы основные термины и определение теории игр?
6. Определите и запишите антагонистическую матричную игру.
7. Каков принцип минимакса?
8. Когда следует использовать смешанные стратегии и как их найти?
9. Понятие и примеры матричных антагонистических игр с нулевой суммой.
10. Задача определения оптимальной смешанной стратегии в антагонистической матричной игре с нулевой суммой и её экономическая интерпретация.
11. Понятие и экономическая интерпретация цены игры. Определение цены матричной антагонистической игры с нулевой суммой.
12. Оптимальные смешанные стратегии: понятие, причины использования, приёмы практической реализации.
13. Подготовка исходных данных для анализа матричной антагонистической игры с нулевой суммой в целях подготовки управленческого решения.
Задания и задачи
Задача 1. Коммерческое предприятие заключило договор на централизованную поставку овощей из теплиц на сумму 10 000 руб. ежедневно. Если в течение дня овощи не поступают, магазин имеет убытки в размере 20 000 руб. от невыполнения плана товарооборота. Магазин может осуществить самовывоз овощей фермера. Для этого он может сделать заказ в транспортном предприятии, что вызовет дополнительные расходы в размере 500 руб. Однако опыт показывает, что в половине случаев посланные машины возвращаются без овощей. Можно увеличить вероятность получения овощей от фермера до 80%, если предварительно посылать туда своего представителя, что требует дополнительных расходов в размере 400 руб. Существует возможность заказать дневную норму овощей у другого надежного поставщика – плодоовощной базы по повышенной на 50% цене. Однако в этом случае, кроме расходов на транспорт (500 руб.), возможны дополнительные издержки в размере 300 руб., связанные с трудностями реализации товара, если в тот же день поступит и централизованная поставка от фермера. Построить игровую модель этой задачи. Какой стратегии надлежит придерживаться магазину, если заранее неизвестно, поступит или не поступит централизованная поставка.
Задача 2. Определить верхнюю и нижнюю цену игры и, если возможно, седловую точку.
| -1 | |||
| -4 | |||
| -2 | -3 | -4 |
Задача 3. Зная платежную матрицу
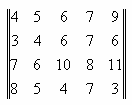
определить нижнюю и верхнюю цены игры и найти решение игры.
Задача 4. Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Однако можно предположить, что его величина характеризуется тремя возможными состояниями (I II III). С учетом этих состояний анализируются три возможных варианта выпуска данной модели (А, Б, В). Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счете различный эффект. Прибыль (тыс. руб.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей
I II III
A= 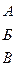
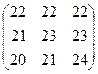

Требуется найти объем выпуска модели одежды, обеспечивающий максимальную величину прибыли при любом состоянии спроса.
Задача 5. Обувная фабрика планирует выпуск двух моделей обуви А и В. Спрос на эти модели не определен, однако можно предположить, что он может принимать одно из двух состояний (I и II). В зависимости от этих состояний прибыль предприятия различна и определяйся матрицей
А= 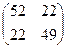
Найдите оптимальное соотношение между объемами выпуска каждой из моделей, при котором предприятию гарантируется максимальная величина прибыли при любом состоянии спроса.
Задача 6. Найти наилучшие стратегии по критериям: максимакса, Вальда, Сэвиджа, Гурвица (коэффициент пессимизма равен 0,2), Лапласа для следующей таблицы возможных доходов.
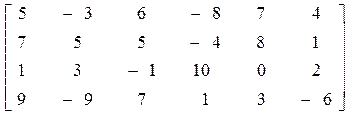
Задача 7. Найдите решение биматричной игры:
а) А= 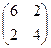 , В=
, В= 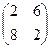 .
.
б) А= 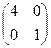 , В=
, В= 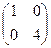 .
.
в) А= 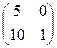 , В=
, В= 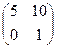 .
.
Дата добавления: 2020-10-25; просмотров: 592;











