Реализация конечных функциональных преобразователей
В данной главе рассматриваются проблемы построения преобразователей информации. Пусть А - некоторое множество элементов информации, представленных тем или иным образом, В - другое множество элементов информации, а Ф - функция преобразования. Преобразователь информации можно представить себе схематически как устройство, реализующее отображение Ф:A®B одного множества на другое (рис.1.1, а). Мы рассмотрим систематические методы построения таких преобразователей. Трудно предложить какое-то решение в общем случае, когда множества А и В имеют произвольную природу, а о самом отображении Ф ничего не известно. Однако, если множества А и В являются конечными (т.е. преобразователь, который мы хотим построить, является “конечным функциональным преобразователем”), существует систематический метод решения этой проблемы, состоящий в том, что элементы множеств А и В предварительно кодируют двоичными кодами и строят преобразование одного множества двоичных векторов в другое (рис.1.1, б).
Двоичное кодирование состоит просто во взаимно однозначном сопоставлении всем элементам конечного множества некоторых двоичных векторов одной и той же длины. При таком подходе проблема реализации преобразователя Ф сводится к построению трех преобразователей: кодировщика К:А®Х, собственно функционального преобразователя F:Х®У и декодировщика D:Y®B, причем эти отображения должны быть выбраны так, что К·F·D=Ф (рис.1.1, б). Рассмотрим проблемы построения этих трех преобразователей поочередно.
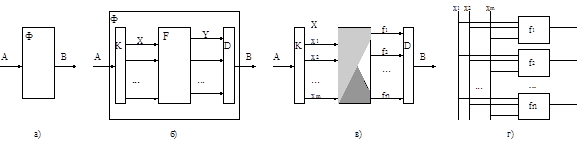
Рис 1.1. Реализация конечного функционального преобразователя
Число двоичных векторов длины n равно 2n, и если все элементы множества S закодировать двоичными векторами одной и той же длины n, то для однозначности кодирования n должно быть не меньше, чем log2|S|. Пусть m и n - длины двоичных векторов для кодирования соответственно множеств А и В входных и выходных информационных элементов конечного функционального преобразователя Ф. Тогда кодирование - это построение некоторого отображения К:А®{0, 1}m, декодирование - построение отображения D:{0, 1}n®B, а функциональное отображение F сопоставляет каждому вектору из :{0, 1}m некоторый вектор из {0, 1}n, причем так, чтобы К·F·D=Ф.
Пример 1.1. Пусть множество А={a1, a2, a3, a4, a5}, a множество B={b1, b2, b3 }, и отображение Ф задается таблицей 1.1.
Тaблица 1.1
Ф:A®B
| А | В |
| a1 | b2 |
| a2 | b3 |
| a3 | b2 |
| a4 | b1 |
| a5 | b2 |
Понятно, что в данном примере m должно быть не меньше 3, n должно быть не меньше 2. Мы можем выбрать произвольно функции кодирования и декодирования (например, Таблицы 1.2 и 1.4). Отображение F строим таким образом, чтобы соотношение К·F·D=Ф выполнялось:
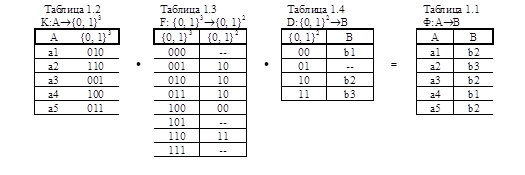
Устройство кодирования должно преобразовать элементы информации множества А заданной природы в двоичные вектора (представленные тем или иным удобным нам способом), причем преобразование это должно быть взаимно однозначно. Аналогично, устройство декодирования должно преобразовать двоичные вектора (представленные тем или иным способом) в элементы информации множества В. Проблема построения конечного функционального преобразователя теперь сводится к реализации произвольного преобразователя F:{0, 1}m®{0, 1}n, который может быть задан, например, таблично, поскольку исходное множество А конечно.
Проблема построения произвольного преобразователя F:{0, 1}m®{0, 1}n имеет более четкую математическую формулировку, однако решить ее непросто. Для упрощения решения этой проблемы удобен следующий простой прием: вместо одной функции F:{0, 1}m®{0, 1}n построить n функций fi:{0,1}m®{0,1} так, что реализация совокупности этих более простых функций даст искомый преобразователь F. Этот прием представлен на рис.1.1, в). На рис. 1.1, г) функции fi выделены явно.
Определение 1.1 Функции вида f:{0, 1}m®{0, 1}, сопоставляющие двоичным векторам двоичные значения, называются двоичными (или булевыми) функциями.ÿ
Если мы сумеем реализовывать любые двоичные функции, в проблеме построения конечных функциональных преобразователей останутся нерешенными только проблемы кодирования и декодирования, которые должны решаться каждый раз по своему при каждом специфическом представлении входной и выходной информации.
1.2. Булевы функции
Несмотря на то, что булевых функций от любого заданного числа m двоичных переменных конечное число (какое?), их слишком много, чтобы иметь запас преобразователей для любых встретившихся отображений. Поэтому основной задачей теории булевых функций является разработка систематического метода построения сложных функций из более простых. Этот метод основан на изучении свойств булевых функций. Рассмотрим сначала все возможные функции от одной двоичной переменной. Их четыре, две из них - константы (0 и 1), одна - тождественная функция, и только одна - функция отрицания (функция НЕ) -является нетривиальной:
НЕ
| p | Øp |
Очевидно, что число различных булевых функций от m переменных равно 2 в степени 2m. При m=2 это число 16, т.е. всего функций от двух переменных 16, однако интересных из них меньше:
Таблица 1.5
| p | q | pÙq | pÚq | pÞq | pÅq | pÛq | p|q | p¯q |
Функция pÙq называется функцией И, или конъюнкцией своих аргументов. Знак конъюнкции часто опускают, иногда в качестве знака конъюнкции используют точку или &. Функция pÚq называется функцией ИЛИ, или дизъюнкцией. Функцию pÞq называют импликацией, или функцией логического следования. Функция pÅq - это функция сложения по модулю два. Функция pÛq называется функцией эквивалентности. Знак эквивалентности иногда обозначают º. Функция p¯q имеет название стрелка Пирсаили функция НЕ-ИЛИ. Функцию p|q называют функцией штрих Шеффера, или функцией НЕ-И.
Суперпозиция двоичных функций может быть записана как формула, которую называют логической формулой.
Пример 1.2. Логическая формула f=((Øp)Úq)Å(rÙqÙ(pÚr)) задает функцию от трех переменных как суперпозицию функций одного и двух переменных.
Для уменьшения числа скобок вводятся приоритеты операций. Наиболее приоритетна функция отрицания. Затем идет конъюнкция, затем дизъюнкция. Все другие функции имеют равный приоритет, меньший, чем у дизъюнкции. Очевидно, что скобками можно установить желаемый порядок операций. Вышеприведенная формула может быть эквивалентно записана так: f=ØpÚqÅrq(pÚr). Отметим, что используют и другое распределение приоритетов, в частности, полагая импликацию менее приоритетной, чем все другие функции.
Логическая формула дает возможность построить соответствующий функциональный преобразователь, если мы имеем “элементарные” или “базисные” преобразователи. Для реализации преобразователя f примера 1.2 необходимо иметь элементы, реализующие отрицание, дизъюнкцию, конъюнкцию и сложение по модулю два.
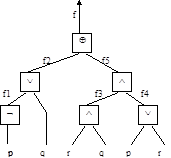
Рис. 1.2. Синтаксическая структура формулы f=ØpÚqÅrq(pÚr) примера 1.2
Очевидным образом по формуле можно построить табличное представление функции f:
Таблица 1.6
| p | q | r | f1=Øp | f2=f1Úq | f3=rÙq | f4=pÚr | f5=f3Ùf4 | f=f2Åf5 |
Очевидно, что суперпозицией нескольких простых функций можно построить более сложную функцию, в частности, функцию от большего числа переменных. Поставим вопрос: можно ли суперпозицией фиксированного набора функций представить любую булеву функцию от любого числа переменных? Удивительно, но ответ на этот вопрос положителен.
Теорема 1.1. Любая двоичная функция может быть представлена как суперпозиция только трех функций: И, ИЛИ и НЕ.
Доказательство этой основной теоремы теории булевых функций основано на свойствах функций И, ИЛИ и НЕ. Их мы сейчас и рассмотрим.
1.3 Свойства булевых функций
Ниже приводятся несколько полезных свойств булевых функций, которые можно легко проверить с помощью таблиц. Две функции Ф и F равны (или эквивалентны), если их значения совпадают на всех наборах их аргументов (обозначать это будем Ф=F).Очевидно, что если Ф и F равны, то ФÛF принимает единичные значения на всех наборах аргументов.
Таблица 1.7
| pÚq = qÚp | pq = qp | коммутативность |
| (pÚq)Úr = pÚ(qÚr) | (pq)r = p(qr) | ассоциативность |
| (pÚq)r = prÚqr | (pq) Úr = (pÚr)(qÚr) | дистрибутивность |
| Ø(pÚq) = ØpØq | Ø(pq) = ØpÚØq | законы де Моргана |
| рØp=0 | рÚØp=1 | законы исключенного третьего |
| (pÚq)p=p | (pq)Úp=p | законы поглощения |
| pÙ0=0 | pÚ0=p | свойства нуля |
| pÙ1=p | pÚ1=1 | свойства единицы |
| ØØp = p | Ø1=0; Ø0=1 | свойства отрицания |
| pÛq=(pÞq) (qÞp) | pÞq=ØpÚq | свойства импликации |
| pÅq=Øpq Ú pØq | 1Åp=Øp | свойства сложения по модулю два |
Доказательство теоремы 1.1 основано на следующей Лемме:
Лемма 1.1. “О дизъюнктивном разложении”. Любая булева функция f(x1, ... хm) от m переменных может быть представлена так: f(x1, ...,хi,...,хm)=Øхif(x1, ...,0,...,хm) Ú хif(x1, ...,1,...,хm)
Доказательство. При хi = 0 правая часть принимает значение Ø0Ùf(x1, ...,0,...,хm) Ú 0Ùf(x1, ...,1,...,хm), что после использования свойств булевых функций элементарно приводится к f(x1, ...,0,...,хm). Аналогично, при хi=1 правая часть приводится к f(x1, ...,1,...,хm).ÿ
Доказательство Теоремы 1.1.Разложим функцию f(x1,...,хm) последовательно по переменным x1, x2,...,хm:
f(x1,...,хm) = Øх1f(0,x2,...,хm) Ú х1f(1,x2,...,хm) = Øх1Øх1f(0, 0, x3,...,хm) Ú Øх1х2f(0, 1, x3,...,хm) Ú х1Øх2f(1,0,x3,...,хm) Ú х1х2f(1,1,...,хm) = ... = Øх1Øх1... Øхmf(0,0,...,0) Ú Øх1Øх1... хmf(0,0,...,1) Ú ... Ú х1х2... хmf(1,1,...,1).
Таким образом, любую булеву функцию можно представить как дизъюнкцию термов, каждый из которых представляет собой конъюнкцию всех переменных (с отрицаниями или без них) и значения этой функции на соответствующем конкретном наборе значений переменных. Обозначим для sÎ{0,1}, xs= Øx при s=0 и xs=x при s=1. Тогда окончательная форма представления любой булевой функции будет иметь вид:
f(x1,...,хm) =ÚsiÎ{0,1} х1s1х2s2...хmsmf(s1,s2,...,sm).
Поскольку значения функции на каждом конкретном наборе равны либо 0, либо 1, то в формуле останутся, очевидно, только такие термы, которые соответствуют наборам переменных, на которых функция равна 1: f(x1,...,хm) = Úf(s1, s2,..., sm)=1х1s1х2s2...хmsm. ÿ
В соответствии с этой теоремой, функция f(p,q,r) = ØpÚqÅrq(pÚr) примера 1.2 на основании ее табличного представления (Таблица 1.6) имеет следующий вид (как суперпозиция функций И, ИЛИ, НЕ): f(p,q,r) = ØpØqØr Ú ØpØqr Ú ØpqØr Ú pqØr.
Хотя эта запись чуть более сложна, чем запись исходной функции, ее неоспоримое преимущество в том, что она выражена через суперпозицию только функцийИ, ИЛИ, НЕ.Более того, такое представление для двоичных функций единственно (с точностью до перестановок термов).
Определение 1.2Функционально полным набором (или базисом) будем называть такое множество двоичных функций, суперпозицией которых могут быть выражены любые булевы функции.
Очевидно, множество булевых функций{И, ИЛИ, НЕ} является базисом: теорема 1.1 говорит о том, что их суперпозицией можно представить любую булеву функцию от любого числа аргументов. Базис{И, ИЛИ, НЕ}называется базисом Буля.
1.4 Нормальные формы представления булевых функций
Определение 1.3. Представление булевой функции в форме дизъюнкции: f(x1,...,хm) = К1Ú К2Ú ...Ú Кn, n³1, где каждый терм Кi (или конъюнкт) представляет собой конъюнкцию (взятых с отрицаниями или без них) двоичных переменных функции, называется дизъюнктивной нормальной формой этой функции (или ДНФ).Если каждый конъюнкт содержит в точности по одной все (взятые с отрицаниями или без них) двоичные переменные функции, ДНФ называется совершенной дизъюнктивной нормальной формой этой функции (или СДНФ).ÿ
Теорема 1.1 гарантирует, что в СДНФ может быть представлена любая булева функция за исключением тождественного нуля.
Теорема 1.2. Представление булевых функций в СДНФ единственно.ÿ
Фактически, две функции можно сравнивать по их СДНФ.
Пример 1.3. Примерами ДНФ функций являются:
Ф1(p,q,r) = ØpØqØr Ú ØpØqr Ú ØpqØr Ú pqØr,
Ф2(p,q,r) = ØpØq Ú pØpØq Ú ØpØr Ú Øpq ,
Ф3(p,q,r) = ØpØq ÚØpØqr Ú qØr.
Первая функция - это СДНФ (и, следовательно, ДНФ) функции f(p,q,r) примера 1.2, вторая содержит терм, куда p входит дважды: с отрицанием и без него. Все три функции равны: все эти формулы представляют одну и ту же функцию, заданную первоначально формулой ØpÚqÅrq(pÚr).ÿ
Существуют другие нормальные представления булевой функции в виде конъюнкции дизъюнкций, полностью симметричные СДНФ и ДНФ.
Определение 1.4. Представление булевой функции в форме конъюнкции: f(x1,...,хm) = D1ÙD2Ù...ÙDn, n ³1, где каждый терм Di представляет собой дизъюнкцию (взятых с отрицаниями или без них) каких-либо двоичных переменных функции (дизъюнктов), называется конъюнктивной нормальной формой этой функции (или КНФ). Если каждый дизъюнкт КНФ содержит в точности по одной все (взятые с отрицаниями или без них) двоичные переменные функции, то такая КНФ называется совершенной конъюнктивной нормальной формой этой функции (или СКНФ).ÿ
Теорема 1.3. Любая булева функция (не равная 1) может быть представлена в CКНФ, причем представление любой функции в СКНФ единственно.
Доказательство теоремы может быть проведено аналогично доказательству теоремы 1.1 на основании следующей леммы Шеннона о конъюнктивном разложении:
Лемма 1.2.(Клод Шеннон, 1938). Любая булева функция f(x1, ...,хi, ... хm) от m переменных может быть представлена так: f(x1, ...,хi,...,хm)=(Øхi Ú f(x1, ...,1,...,хm) ) Ù ( хi Ú f(x1, ...,0,...,хm) ).
Проверить справедливость леммы 1.2 можно простой подстановкой возможных значений переменной хi.Доказательство леммы и теоремы остается для самостоятельной работы читателя.ÿ
Преобразование в нормальную форму.Всякая аналитическая запись функции может быть преобразована в нормальную форму. Приведем систематическую процедуру преобразования функции в нормальную форму с использованием свойств двоичных функций из табл. 1.7.
Шаг 1. Используем свойства pÛq=(pÞq)(qÞp), pÞq=ØpÚq, pÅq=Øpq Ú pØq для того, чтобы устранить операции Û, Þ, Å, оставив только операцииИ, ИЛИ, НЕ.
Шаг 2. Используем свойства отрицания и законы де Моргана: Ø(pÚq) = ØpØq, Ø(pq) = ØpÚØq, чтобы операция отрицания стояла непосредственно перед переменными.
Шаг 3. Используем свойства дистрибутивности и другие свойства, чтобы получить нормальную форму.Заметим, что для получения СКНФ часто нужно использовать следующее свойство дистрибутивности: (pq) Úr = (pÚr)(qÚr)ÿ
Пример 1.4. Преобразуем аналитически функцию f(p,q,r) = ØpÚqÅrq(pÚr) примера 1.2 в СКНФ.
Применяя шаги процедуры, получим:
f(p,q,r) = ØpÚqÅrq(pÚr) = (Ø(ØpÚq)rq(pÚr))Ú(ØpÚq)Ø(rq(pÚr)) = pØqrq(pÚr)Ú(ØpÚq)(ØrÚØqÚ(ØpØr)) = (ØpÚq)(ØrÚØqÚ(ØpØr)) = (ØpÚq)(ØrÚØqÚØp)(ØrÚØqÚØr) = (ØpÚq)(ØqÚØr).
Таким образом, мы получили КНФ функции f(p,q,r). Чтобы получить ее СКНФ, нужно каждый дизъюнкт, в котором не хватает какой-либо переменной, повторить дважды: с этой переменной и с ее отрицанием: f(p,q,r) = (ØpÚqÚr)(ØpÚqÚØr)(pÚØqÚØr)(ØpÚØqÚØr).ÿ
1.5Реализация двоичных функций
Основная проблема в реализации двоичных функций - это проблема адекватного представления дискретных значений 0 и 1 с помощью физических величин, имеющих обычно непрерывный диапазон изменений. В электрической цепи значения 0 и 1 удобно представлять соответственно низким и высоким уровнями тока или напряжения. Наиболее естественно использовать для этого ключ-реле. Следующий рисунок показывает, как с помощью электромеханического реле представить все три базовые двоичные функции.
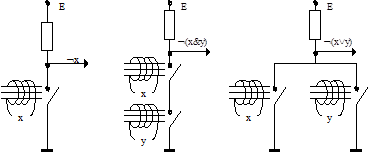
В настоящее время роль электронного ключа без механических деталей выполняет так называемый вентиль, или транзисторный переход. Совокупность вентилей изготовляется на кремниевой подложке с высокой степенью интеграции. В одном блоке - чипе - в настоящее время может помещаться схема из 106 и более транзисторных переходов. Современная технология позволяет с использованием только одного вида вентилей изготавливать на одной подложке крупные узлы вычислительной техники: процессоры, память, и т.п. Возможность автоматизированного построения в едином технологическом цикле логических схем огромной сложности стало главной причиной последних революционных изменений в области всей вычислительной техники.
Элементарные схемы функций базиса Буля изображаются так:
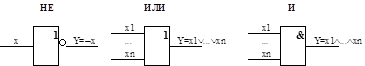
Рис 1.3. Изображение схем, реализующих функции базиса Буля
1.6 Минимизация булевых функций
Сложность схемы, реализующей булеву функцию, определяется сложностью ее аналитической записи. Поскольку одну и ту же булеву функцию можно представить различными формулами, то задача выбора наиболее простой формулы, задающей булеву функцию, непосредственно ведет к наиболее простой схеме, т.е., в частности, к экономии материалов, объема, веса и энергопотребления схемы. Минимальной формой булевой функции в некотором базисе можно считать такую, которая содержит минимальное число суперпозиций функций базиса, допуская и скобки. Однако, построить эффективный алгоритм такой минимизации с получением минимальной скобочной формы трудно.
Рассмотрим более простую задачу минимизации при синтезе комбинационных схем, при которой ищется не минимальная скобочная форма функции, а ее минимальная ДНФ. Для этой задачи существуют простые эффективные алгоритмы. Рассмотрим два из них.
Метод Квайна. Минимизируемая функция представляется в СДНФ, и к ней применяются все возможные операции неполного склеивания KxÚKØx = KÚKxÚKØx, а затем поглощения KÚKx = K, и эта пара этапов применяется многократно.
Карта Карно. Это двумерная табличная форма представления булевой функции, позволяющая легко в графической наглядной форме отыскать минимальные ДНФ логических функций. Каждой клетке в таблице сопоставляется терм СДНФ минимизируемой функции, причем так, что любым осям симметрии таблицы соответствуют зоны, взаимно инверсные по какой-либо переменной. Такое расположение клеток в таблице позволяет легко определить склеивающиеся термы СДНФ (отличающиеся знаком инверсии только одной переменной: они располагаются в таблице симметрично. В таблице рис.1.4, б) представлена карта Карно для функции двух переменных - импликации. Все 4 клетки соответствуют всем возможным конъюнкциям СДНФ функции двух переменных. Единичные значения функции показывают те термы, которые присутствуют в СДНФ этой функции. Расположения термов для карты Карно функции двух переменных (рис.1.4, а) таково, что соседние клетки соответствуют склеивающимся термам, отличающимся только одной переменной: в один конъюнкт эта переменная входит без отрицания, а в другой - с отрицанием. В соответствии с рис.1.4, б), импликацию можно представить минимальной ДНФ: ØxÚу.
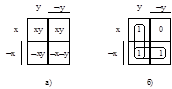
Рис.1.4 Карта Карно для импликации xÞy
На рис. 1.5 а) представлена карта Карно функции f(p,q,r) = ØpÚqÅrq(pÚr) примера 1.2 на основании ее табличного представления (Таблица 1.6). Ее минимальная ДНФ из рис. 1.5 а) равна qØrÚØpØq.
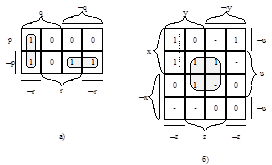
Рис.1.5 Карта Карно функций 3-х и 4-х переменных
Карты Карно удобны для минимизации и неполностью определенных функций. Например, на рис 1.5 б) представлена функция 4-х переменных, у которой не определены 5 значений. Неопределенные значения можно заменить любыми - 0 или 1. Следовательно, функцию на рис. 1.5 б) можно заменить любой из 32-х полностью определенных функций. Покрывая таблицу минимальным числом максимальных квадратов (или прямоугольников) со сторонами, равными степени двойки, так, чтобы они обязательно покрыли все единицы и не покрывали ни одного нуля, получим следующую минимальную ДНФ всех возможных функций, представленных на этой диаграмме: хØzÚzu.
Пример 1.5. Таблица 1.8 повторяет таблицу 1.3, представляя частичное отображение F из множества трехразрядных двоичных векторов в множество двухразрядных двоичных векторов примера 1.1. Две двоичные функции f1 и f2 представляют соответствующие разряды результата отображения F.
Таблица 1.8
| x | y | z | f1 | f2 |
| - - - | - - - |
Из карт Карно рис. 1.6 легко видеть, что минимальные ДНФ этих функций имеют вид: f1 = yÚØx, и f2 = xy.ÿ
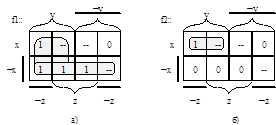
Рис.1.6 Карта Карно для функций f1 и f2 примера 1.5
Пример 1.6. Схема отображения в микрокалькуляторе. Рассмотрим задачу построения схемы отображения цифр, которые набирает пользователь нажимая клавиши на клавиатуре микрокалькулятора, в их изображение (рис.1.7). Двоичное кодирование цифр осуществляется непосредственно в момент нажатия клавиши в четырехразрядный двоично-десятичный код. Декодирование изображений осуществляется семисегментной структурой светодиодов, специальное расположение которых позволяет высвечивать различные цифры: подача напряжения на соответствующую полоску f0 - f6 вызывает ее свечение. Непосредственно логическая схема отображения СО имеет четыре двоичных входа и семь двоичных выходов (по числу сегментов светодиодов).

Рис.1.7. Отображение цифр в микрокалькуляторе (а); семисегментная структура светодиодов
для отображения цифры (б); и один разряд схемы отображения (в).
Кроме десяти цифр со стандартным двоично-десятичным кодированием пусть в схеме возможно представить знак минус кодом <1111>. Семь двоичных функций f0-f6 представлены таблицей истинности 1.9; функции эти неполностью определены, поскольку коды, не соответствующие десятичным цифрам и знаку минус не могут появиться на входе схемы отображения. Мы можем дополнить их произвольными значениями исходя, например, из критерия минимальности функции. Заполнение таблицы 1.9 очевидно: например, для изображения цифры 5 (двоичный код на входе СО <0101>) следует подать напряжение на все полоски светодиодов, кроме f3 и f6.
Таблица 1.9
| x1 | x2 | x3 | x4 | f0 | f1 | f2 | f3 | f4 | f5 | f6 |
| - - - - - | - - - - - | - - - - - | - - - - - | - - - - - | - - - - - | - - - - - |
Минимизация неполностью определенных функций f0-f6 может быть легко проведена с помощью карт Карно.
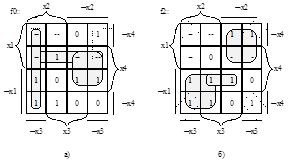
Рис. 1.8. Карты Карно функций f0 и f2
схемы отображения микрокалькулятора
На рис 1.8 приведены две карты Карно функций f0 и f2. После минимизации можем записать:
f0= х1х4ÚØх2х4Úх2Øх3Úх2Øх4Úх1Øх3;
f2= Øх1х2Úх1Øх2ÚØх3Øх4ÚØх1х3х4.
В выпускаемых промышленностью схемах отображения присутствует также дополнительный вход для высвечивания десятичной точки и другой вход для подавления изображения незначащих нулей в старших разрядах числа. ÿ
Для минимизации функций пяти и более переменных использование карт Карно затруднено во первых, большей громоздкостью таблиц, и, во-вторых, тем, что при большем, чем 2 переменных, не удается расположить все склеиваемые термы рядом. Тем не менее, и для пяти, и для шести переменных использование этого подхода полезно. Карты Карно используются во многих приложениях. Один из удачных примеров применения этого подхода для решения проблемы анализа и синтеза законов управления в системе “Импульсный усилитель мощности - электродвигатель” приведен в [БП96]. Приведем еще один пример использования карт Карно.
Пример 1.7. Рассмотрим проблему словесной формулировки условия достижения консенсуса (общего согласия) в вычислительной сети [TS92]. Проблема ставится следующим образом. Возможность достижения консенсуса в сети зависит от четырех параметров сети:
· тип процессоров; процессоры могут быть асинхронными (А) или синхронными (С);
· сохранение порядка сообщений в канале: {порядок сохраняется (П), либо без сохранения (Б)};
· вид передачи сообщений: {широковещательная передача (Ш), точка-точка (Т)};
· ограничение коммуникации во времени: { коммуникация ограничена (О), не ограничена (Н)}.
Исследования [TS92] показали, что консенсус достижим только в сетях со следующими наборами параметров: (А,П,Ш,Н), (А,П,Ш,О), (С,Б,Т,О), (С,Б,Ш,О), (С,П,Ш,Н), (С,П,Ш,О), (С,П,Т,Н), (С,П,Т,О). Как коротко сформулировать условия достижимости консенсуса в вычислительных сетях?
На основе теории двоичных функций это можно сделать не понимая, что такое консенсус, и не имея никакого представления о вычислительных сетях. Построим карту Карно двоичной функции Консенсус четырех двоичных переменных, каждая из которых соответствует одному из указанных параметров.
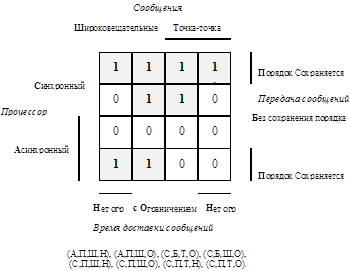
Простая минимизация дает следующее выражение этой функции: СПÚСОÚШП=С(ПÚО) ÚШП. Выразим эту формулу на естественном языке: "Консенсус достижим только в вычислительных сетях с синхронным процессором, в которых или сохраняется порядок сообщений, или есть ограничения коммуникации по времени, а также в таких сетях, в которых возможна широковещательная передача сообщений с сохранением их порядка". Возможны и другие, эквивалентные формулировки.ÿ
1.7 Функциональная полнота. Теорема Поста
В соответствии с определением 1.2,функционально полным набором (или базисом) называется такое множество булевых функций, суперпозицией которых могут быть выражены любые булевы функции. Один из таких базисов - базис Буля - нами определен: это три функции И, ИЛИ, НЕ. Исследование проблем, связанных с базисами, чрезвычайно важно для практики: функции базиса - это тот полный набор строительных блоков, из которых можно строить все другие двоичные функции от любого числа переменных, а следовательно, реализовывать любые конечные функциональные преобразователи.
Важными для практики и интересными с теоретической точки зрения являются вопросы:
· почему функции И, ИЛИ, НЕ такие особенные, что с их помощью можно построить любую другую булеву функцию?
· существуют ли еще какие-нибудь базисы, кроме базиса Буля?
· является ли некоторый заданный базис минимальным (т.е. не содержит ли он излишних функций, выражающихся суперпозицией других)?
· как проверить, является ли заданный набор функций базисом, и если нет, как дополнить его другими функциями, чтобы получившееся множество составило базис?
Введем некоторые определения и обозначения.
Определение 1.5. Замыканием множества М булевых функций назовем такое множество булевых функций, которые можно получить суперпозицией функций из М. Замыкание множества М обозначим [M]. ÿ
Пусть В -множество всех двоичных функций. Очевидно, что множество М двоичных функций будет базисом, только если [M]=В. Рассмотрим свойства замыканий двоичных функций.
Теорема 1.4. Пусть М, NÍВ.
а) МÍ[M];
б) [[M]] = [M]; [В] = В;
в) MÍNÞ[M] Í[N];
г) [M] ÍВ;
д) если М - базис и MÍ[N], то N - тоже базис.
Доказательство теоремы просто. Утверждения а), б), в) и г) следуют непосредственно из определений. Докажем д). MÍ[N] Þ [M] Í[[N]] на основании в), следовательно, [M] Í[N] на основании б). Но поскольку М- базис, [M]=В. Отсюда, ВÍ[N], но поскольку (г) [N] ÍВ, то [N]=В.ÿ
Попробуем найти другие базисы, отличные от базиса Буля. Согласно законам де Моргана, Ø(pÚq) = ØpØq. Следовательно, pÚq= Ø(ØpØq). Таким образом, дизъюнкция выражается через конъюнкцию и отрицание, следовательно, суперпозицией функций {И, НЕ}можно построить все функции базиса Буля - т.е. ИЛИможно выбросить из этого базиса. Некоторые другие базисы представлены в таб.1.10. Их обоснование очевидно.
Таблица 1.10
| Обоснование | Базис |
| Ø(pÚq) = ØpØq; Следовательно, pÚq = Ø(ØpØq); | {И, НЕ} - конъюнктивный базис |
| Ø(pq) = ØpÚØq; Следовательно, pq= Ø(ØpÚØq); | {ИЛИ, НЕ} - дизъюнктивный базис |
| Øp = pÅ1; | {И, Å, 1} - базис Жегалкина |
| p|q = Ø(pq); Следовательно, Øp = p|p; pq = Ø(p|q) = (p|q)|(p|q); | {|} - базис Шеффера |
| p¯q = Ø(pÚq) Следовательно, Øp = p¯p; pÚq = Ø(p¯q) = (p¯q) ¯(p¯q); | {¯} - базис Пирса |
Рассмотрим конъюнктивный базис. Он является минимальным, поскольку выбрасывание из множества {И, НЕ}любой функции превращает оставшееся одноэлементное множество не в базис. Действительно, например, с помощью суперпозиции произвольного числа функций НЕ можно построить только функцию НЕ и тождественную функцию ИДЕНТ, т.е. f(x)=x. Заметим, что суперпозицией унарных функций множества М = {ИДЕНТ, НЕ} можно построить только функции этого множества. Множество булевых функций, обладающее этим свойством, называется замкнутым классом двоичных функций.
Пример 1.8. Конъюнкции, т.е. все функции вида x1Ùx2Ù...Ùxm, тоже составляют замкнутый класс. Очевидно, однако, что, например, функцию, которая на наборе (0,0,...,0) имеет значение 1, нельзя представить суперпозицией таких функций. Таким образом, конъюнктивный базис {И, НЕ}является минимальным. ÿ
Более подробно рассмотрим базис Жегалкина.
Дата добавления: 2016-07-27; просмотров: 2777;











