Модели и характеристики апериодических и интегрирующих измерительных преобразователей
Характеристики многих измерительных преобразователей (ИП) независимо от физической природы их функционирования удается аппроксимировать характеристикой апериодической модели. Такие преобразователи иногда называют инерционными ИП первого порядка или реальными интегрирующими ИП, а в некоторых случаях – фильтрами нижних частот.
На рис. 6.1, а приведена схема пневматического ЭИП, состоящего из круглой трубки длиной l и диаметром d, а также глухой камеры объемом Vk. Принимаем давление p газа на входе трубки за входную величину, а за выходную – перемещение h подвижного жесткого центра упругой мембраны, которое соответствует давлению pk газа в камере: 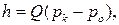 где pо – опорное давление. Считая параметры сосредоточенными и, пренебрегая инерционностью и объемом газа в трубке, можно записать дифференциальное уравнение в линейной интерпретации для малых отклонений давления от некоторого уровня в виде соотношения баланса давлений
где pо – опорное давление. Считая параметры сосредоточенными и, пренебрегая инерционностью и объемом газа в трубке, можно записать дифференциальное уравнение в линейной интерпретации для малых отклонений давления от некоторого уровня в виде соотношения баланса давлений
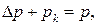
где 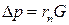 – падение давления на трубке, Па;
– падение давления на трубке, Па; 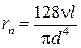 – пневматическое сопротивление трубки в соответствии с формулой Пуазейля,
– пневматическое сопротивление трубки в соответствии с формулой Пуазейля, 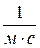 ; ν – кинематическая вязкость газа,
; ν – кинематическая вязкость газа, 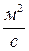 ;
; 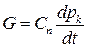 – массовый расход газа через трубку,
– массовый расход газа через трубку, 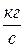 ;
; 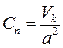 – пневматическая емкость камеры, м·с2; a– скорость звука,
– пневматическая емкость камеры, м·с2; a– скорость звука, 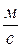 .
.
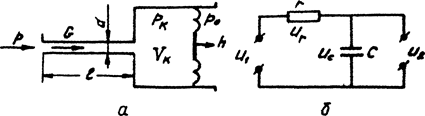
Рис.6.1. Принципиальная схема пневматического ИП (а)
и электрическая схема его замещения (б).
Выражая Δp через первичные параметры и переходя к операторной форме записи, получим:
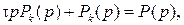 (6.1)
(6.1)
где 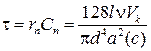 – постоянная времени апериодической модели пневматического ИП.
– постоянная времени апериодической модели пневматического ИП.
Операторная чувствительность модели пневматического ЭИП определяется выражением
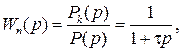 (6.2)
(6.2)
а результирующая чувствительность преобразователя с учетом 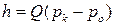 имеет вид
имеет вид
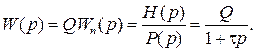 (6.3)
(6.3)
На рис. 6.1, б в виде упрощенной динамической модели приведена электрическая схема замещения пневматического ИП, которая полностью совпадает со схемой ненагруженного электрического фильтра rC нижних частот. Пневмоэлектрическая аналогия хорошо согласуется при замене давлений p электрическими напряжениями U, а массовых расходов G газа – электрическими токами i. Потери энергии определяются коэффициентами потерь – пневматическим и электрическим сопротивлениями rn и r, а возможность накопления энергии характеризуется пневматической и электрической емкостями Cn и C.
Естественно, что дифференциальные уравнения и операторные чувствительности ИП полностью совпадают. Уравнение баланса напряжений 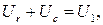 где
где 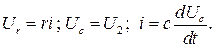 Тогда
Тогда 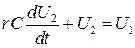 и
и 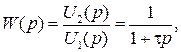 где
где 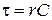 – постоянная времени фильтра.
– постоянная времени фильтра.
К виду чувствительности, аналогичному (6.3), приводятся динамические характеристики электромеханических ИП (например электродвигателей), термоэлектрических, турбоанемометрических и других типов ИП.
Измерительные преобразователи, описываемые апериодической моделью, нередко используются для безынерционного преобразования сигналов в полосе сравнительно низких частот (от 0 до ωn) или в качестве фильтров нижних частот. В этом случае стремятся максимально уменьшить постоянную времени τ, а дифференциальная (статическая) чувствительность преобразователя определяется выражением 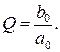 При использовании таких преобразователей в качестве интегрирующих (реальных) в полосе сравнительно высоких частот постоянную времени увеличивают, но учитывают, что динамическая чувствительность такого преобразователя обратно пропорциональна постоянной времени
При использовании таких преобразователей в качестве интегрирующих (реальных) в полосе сравнительно высоких частот постоянную времени увеличивают, но учитывают, что динамическая чувствительность такого преобразователя обратно пропорциональна постоянной времени
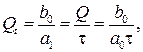 (6.4)
(6.4)
так как
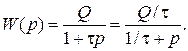
Комплексную чувствительность апериодической модели ИП можно записать в виде:
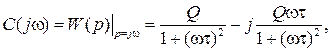 (6.5)
(6.5)
где действительная часть 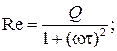 мнимая часть
мнимая часть 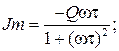 амплитудная чувствительность или амплитудно-частотная характеристика (АЧХ)
амплитудная чувствительность или амплитудно-частотная характеристика (АЧХ)
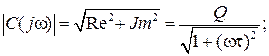 (6.6)
(6.6)
угловое положение комплексного вектора определяет фазовую чувствительность или фазо-частотную характеристику (ФЧХ)
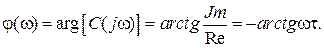 (6.7)
(6.7)
В показательной форме комплексная чувствительность принимает вид:
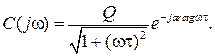 (6.8)
(6.8)
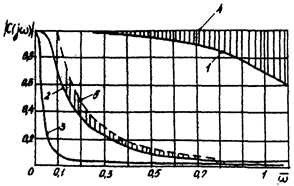
На рис. 6.2, а приведена векторная диаграмма комплексной чувствительности апериодической модели ИП в виде полуокружности с диаметром равным Q, которая расположена в 4-м квадранте комплексной плоскости.
В качестве аргумента частотных характеристик удобно принять безразмерную частоту 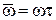 , которая связывает в единый комплекс как частотную характеристику входного сигнала – его круговую частоту ω, так и динамические свойства собственно модели ИП – ее постоянную времени τ.
, которая связывает в единый комплекс как частотную характеристику входного сигнала – его круговую частоту ω, так и динамические свойства собственно модели ИП – ее постоянную времени τ.
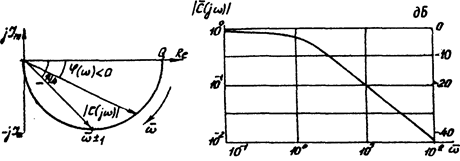
а) б)
в) г)
Рис.6.2. Частотные характеристики апериодической модели ИП.
Амплитудные значения |C(jω)| комплексной чувствительности также рационально представлять в безразмерной форме путем приведения их к характерным значениям, в частности, для апериодической модели – к значению чувствительности при ω→0, т. е. к |C(0)|:
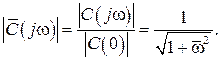 (6.9)
(6.9)
Безразмерная форма представления характеристик апериодической модели в виде единых обобщенных зависимостей или графиков позволяет охватить множество различных по параметрам "апериодических" ИП.
При определении результирующей чувствительности 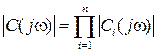 последовательно соединенных ЭИП с целью сведения операции умножения к операции суммирования
последовательно соединенных ЭИП с целью сведения операции умножения к операции суммирования 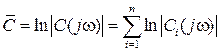 амплитудные чувствительности представляют в логарифмическом масштабе, как это показано на рис. 6.2, б. Если берется натуральный логарифм, то амплитудные затухания
амплитудные чувствительности представляют в логарифмическом масштабе, как это показано на рис. 6.2, б. Если берется натуральный логарифм, то амплитудные затухания 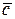 исчисляют в неперах, при десятичном логарифме – в беллах или уменьшенных в 10 раз единицах – децибелах (дБ): 1Неп=8,686дБ.
исчисляют в неперах, при десятичном логарифме – в беллах или уменьшенных в 10 раз единицах – децибелах (дБ): 1Неп=8,686дБ.
Затухание 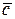 сигналов при мощности W при одинаковых значениях коэффициентов потерь (активных сопротивлений) на входе и выходе ЭИП определяют следующей зависимостью:
сигналов при мощности W при одинаковых значениях коэффициентов потерь (активных сопротивлений) на входе и выходе ЭИП определяют следующей зависимостью:
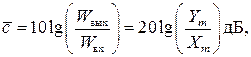
так как связь амплитудных значений сигналов и их мощностей является квадратичной:
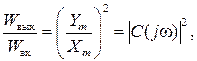 (6.10)
(6.10)
где 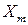 и
и 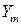 – амплитудные значения входного и выходного сигналов;
– амплитудные значения входного и выходного сигналов; 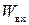 и
и 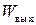 – входная и выходная мощности.
– входная и выходная мощности.
Если безразмерную частоту 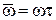 представить также в логарифмическом масштабе, то амплитудная чувствительность апериодической модели хорошо аппроксимируется двумя прямыми: первой – от 0 до
представить также в логарифмическом масштабе, то амплитудная чувствительность апериодической модели хорошо аппроксимируется двумя прямыми: первой – от 0 до 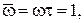 почти горизонтальной, с результирующим затуханием
почти горизонтальной, с результирующим затуханием 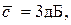 и второй, наклоненной под углом
и второй, наклоненной под углом 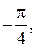 т. е. с затуханием
т. е. с затуханием 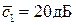 на декаду (-6дБ на октаву). Представление чувствительностей прямыми упрощает решение задач анализа и синтеза сложных ИП.
на декаду (-6дБ на октаву). Представление чувствительностей прямыми упрощает решение задач анализа и синтеза сложных ИП.
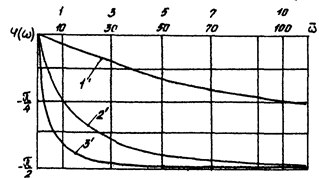
На рис. 6.2, в и г приведены амплитудные и фазовые чувствительности апериодической модели ИП в изменяющемся по оси абсцисс десятичном масштабе. Кривые 1, 2 и 3, а также 1¢, 2¢ и 3¢ частотных характеристик приведены в соответствии с масштабами 1, 10, 100 по оси абсцисс; они представляют единую обобщенную характеристику, не пересекаются и позволяют наглядно изучать задачи как в большом, так и в малом диапазоне безразмерных частот. Кривыми 4 и 5 представлены характеристики безынерционных моделей преобразователя – соответственно пропорциональной 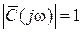 и интегрирующей
и интегрирующей 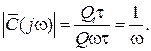
Переходную чувствительность (переходную функцию или функцию включения) 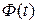 апериодической модели преобразователя определяют непосредственно решением дифференциального уравнения модели или путем обратного преобразования (L-1) операторной чувствительности W(s), представленной выражением (6.3) как функцию времени выходного сигнала y(t) при изменении входного сигнала скачком от x=0 при t<0 до x=x1=const при t≥0:
апериодической модели преобразователя определяют непосредственно решением дифференциального уравнения модели или путем обратного преобразования (L-1) операторной чувствительности W(s), представленной выражением (6.3) как функцию времени выходного сигнала y(t) при изменении входного сигнала скачком от x=0 при t<0 до x=x1=const при t≥0:
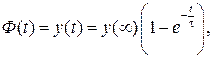 (6.11)
(6.11)
где 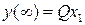 при
при 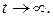 При единичном (безразмерном) скачке
При единичном (безразмерном) скачке 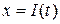 получим переходный процесс, представленный в безразмерном виде переходной чувствительностью
получим переходный процесс, представленный в безразмерном виде переходной чувствительностью
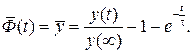 (6.12)
(6.12)
Тогда импульсная переходная чувствительность (функция веса или импульсная переходная функция) f(t) определяется выражением
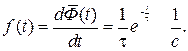 (6.13)
(6.13)
На рис. 6.3 приведены графики изменения во времени входного сигнала в виде скачков
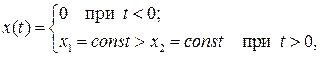
а также соответственно выходных сигналов
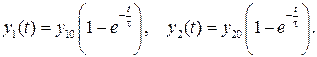
В начальном интервале времени, когда 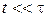 , изменение выходного сигнала апериодической модели достаточно хорошо отражает функцию идеального интегрирования входного сигнала, представленную на графике прямыми 1 и 2:
, изменение выходного сигнала апериодической модели достаточно хорошо отражает функцию идеального интегрирования входного сигнала, представленную на графике прямыми 1 и 2:
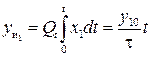 или
или 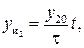 (6.14)
(6.14)
где 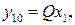
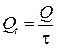 – динамическая чувствительность интегрирующего преобразователя; Q – статическая чувствительность; x1 – входная величина.
– динамическая чувствительность интегрирующего преобразователя; Q – статическая чувствительность; x1 – входная величина.
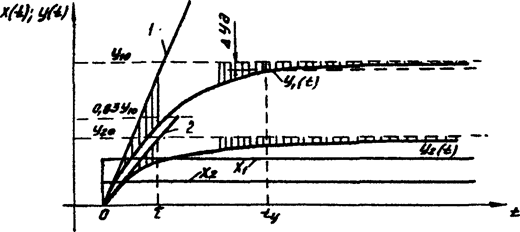
Рис.6.3. Переходной процесс апериодического ЭИП.
С течением времени погрешность Δyи интегрирования увеличивается (на рис. 6.3 ординаты погрешностей показаны штриховкой):
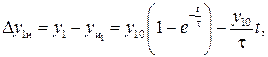 (6.15)
(6.15)
или при разложении 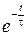 в ряд погрешность интегрирования определится в относительном виде:
в ряд погрешность интегрирования определится в относительном виде:
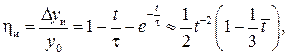 (6.16)
(6.16)
где 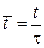 – безразмерное время.
– безразмерное время.
При 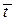 = 0,1; 0,2; 0,3; 0,5; 1,0 соответственно имеют место погрешности интегрирования ηи = 0,5; 2; 4; 10; 37%. При допустимой погрешности интегрирования
= 0,1; 0,2; 0,3; 0,5; 1,0 соответственно имеют место погрешности интегрирования ηи = 0,5; 2; 4; 10; 37%. При допустимой погрешности интегрирования
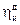 = 5% такой интегратор возможно использовать в течение времени, ограниченного значением
= 5% такой интегратор возможно использовать в течение времени, ограниченного значением 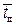 = 0,35.
= 0,35.
Если апериодическая модель ЭИП используется как безынерционная в нижней полосе частот, тогда при изменении входного сигнала скачком выходной сигнал имеет динамическую погрешность, уменьшающуюся с течением времени (ординаты погрешностей Δy<0 на рис. 6.3 отмечены штриховкой для t>τ):
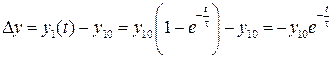 (6.17)
(6.17)
или в виде относительной погрешности:
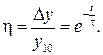 (6.18)
(6.18)
Определим время tу установления выходного сигнала, при котором погрешность η не превышает допустимого значения ηд, т. е. при 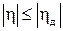 :
:
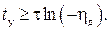 (6.19)
(6.19)
Так, для допустимых погрешностей ηд= – 0,37; – 0,05; – 0,01 получим соответствующее время установления tу ≥ 1τ; 3τ; 5τ.
Если входной сигнал x0=0 в момент t0=0 начинает изменяться с постоянной скоростью 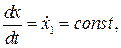 т. е.
т. е. 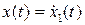 , тогда выходной сигнал, учитывая (6.13), можно определить интегралом свертки
, тогда выходной сигнал, учитывая (6.13), можно определить интегралом свертки
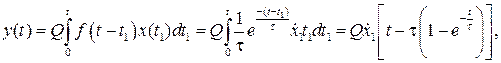 (6.20)
(6.20)
где Q – дифференциальная чувствительность; t1 – координата отсчета времени моментов импульсов.
В переходном режиме погрешность апериодической модели определится зависимостью
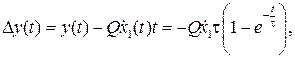 (6.21)
(6.21)
при t>>τ имеет место установившейся режим, при котором погрешность определяется произведением 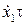 , т. е.
, т. е. 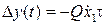 .
.
Графическая интерпретация этих погрешностей дана на рис. 6.1 в виде приведенной погрешности δ для интервала времени 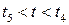 . В интервале времени
. В интервале времени 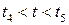 погрешность определяется зависимостью
погрешность определяется зависимостью
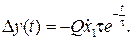 (6.22)
(6.22)
Динамические погрешности при гармонических входных сигналах удобно оценивать, определяя амплитудные погрешности и фазовые сдвиги. С этой целью используют частотные характеристики (рис. 6.2). Заметим, что мгновенные динамические погрешности могут принимать значительно большие значения по сравнению с амплитудными.
Если апериодический ЭИП используют как безынерционный в нижней полосе частот, то относительная амплитудная погрешность ηа определяется разницей ординат кривых 1 и 4 (на рис. 6.2, в заштрихована), т. е.
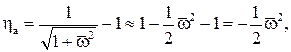 (6.23)
(6.23)
где 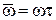 – безразмерная частота.
– безразмерная частота.
На участке частот 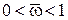 фаза определяется кривой 1’(рис. 6.2, г), т. е.
фаза определяется кривой 1’(рис. 6.2, г), т. е. 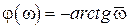 , которую можно аппроксимировать прямой. Так как задержка во времени Δt1 выходного сигнала пропорциональна фазовой чувствительности преобразователя
, которую можно аппроксимировать прямой. Так как задержка во времени Δt1 выходного сигнала пропорциональна фазовой чувствительности преобразователя 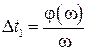 , выраженной в единицах времени (с), тогда при линейной фазовой чувствительности
, выраженной в единицах времени (с), тогда при линейной фазовой чувствительности 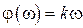 , где k – постоянный коэффициент пропорциональности, время задержки
, где k – постоянный коэффициент пропорциональности, время задержки 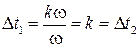 не зависит от частоты в принятом диапазоне линейности. Следовательно, линейно увеличивающееся запаздывание по фазе (с линейной ФЧХ в упомянутой полосе частот) означает неизменную во времени задержку всех частотных составляющих сложного входного сигнала x(ω), что будет существенно искажать на выходе форму входного сигнала, т. е. на практике в ряде случаев может не учитываться как погрешность. Однако при больших
не зависит от частоты в принятом диапазоне линейности. Следовательно, линейно увеличивающееся запаздывание по фазе (с линейной ФЧХ в упомянутой полосе частот) означает неизменную во времени задержку всех частотных составляющих сложного входного сигнала x(ω), что будет существенно искажать на выходе форму входного сигнала, т. е. на практике в ряде случаев может не учитываться как погрешность. Однако при больших 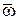 имеют место не только большие фазовые, но и амплитудные погрешности. В этом случае апериодическая модель преобразователя, занижая амплитудные значения гармонических составляющих входного сигнала, тем самым осредняет их, т. е. интегрирует. Амплитудная чувствительность
имеют место не только большие фазовые, но и амплитудные погрешности. В этом случае апериодическая модель преобразователя, занижая амплитудные значения гармонических составляющих входного сигнала, тем самым осредняет их, т. е. интегрирует. Амплитудная чувствительность 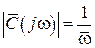 безынерционной (идеальной) интегрирующей модели ЭИП является гиперболой, поэтому амплитудная относительная погрешность ηа определится разницей ординат кривых 2 и 5 (на рис. 6.2, в заштрихована), которая для
безынерционной (идеальной) интегрирующей модели ЭИП является гиперболой, поэтому амплитудная относительная погрешность ηа определится разницей ординат кривых 2 и 5 (на рис. 6.2, в заштрихована), которая для 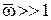 запишется выражением
запишется выражением
 (6.24)
(6.24)
На рис. 6.4 приведены кривые относительных амплитудных погрешностей ηа апериодической модели при использовании преобразователя в качестве безынерционого (кривая 1) в нижней полосе частот, а также интегрирующего (кривая 2) ИП в верхней полосе частот.
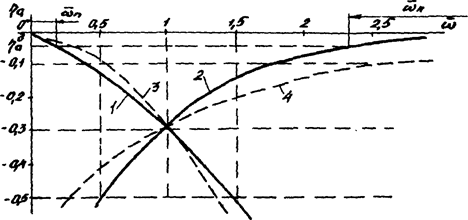
Рис. 6.4. Амплитудные погрешности
Для допустимого значения погрешности ηд = –0,05 получим проходные полосы безразмерных частот: в первом случае 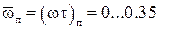
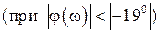 , во втором случае
, во втором случае 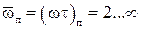 (при
(при 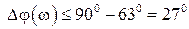 ). Соответственно при выражении частот в герцах:
). Соответственно при выражении частот в герцах: 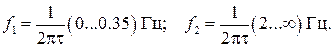
Дата добавления: 2020-10-25; просмотров: 600;











