Интегрирование рациональных дробей с помощью разложения на простейшие дроби.
Перед интегрированием рациональной дроби Р(x)/Q(х) надо сделать следующие алгебраические преобразования и вычисления:
1) если дана неправильная рациональная дробь, то выделить из нее целую часть, т.е. представить в виде
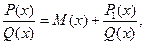
где М (х) – многочлен, a 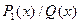 – правильная рациональная дробь;
– правильная рациональная дробь;
2) разложить знаменатель дроби на линейные и квадратичные множители:
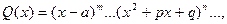
где 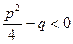 , т. е. трехчлен
, т. е. трехчлен 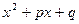 имеет комплексные сопряженные корни;
имеет комплексные сопряженные корни;
3) правильную рациональную дробь разложить на простейшие дроби:
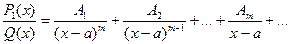
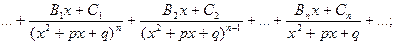
4) вычислить неопределенные коэффициенты
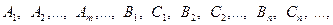 для чего привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов.
для чего привести последнее равенство к общему знаменателю, приравнять коэффициенты при одинаковых степенях х в левой и правой частях полученного тождества и решить систему линейных уравнений относительно искомых коэффициентов.
В результате интегрирование рациональной дроби исходный интеграл сведется к нахождению интегралов от многочлена и от простейших рациональных дробей.
Например, найдем интеграл 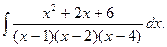
Так как каждый из двухчленов 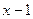 ,
, 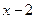 ,
, 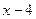 входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы простейших дробей I типа:
входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде суммы простейших дробей I типа:
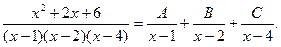
Освобождаясь от знаменателей, получим
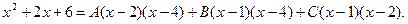
Следовательно,
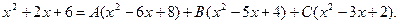
Сгруппируем члены с одинаковыми степенями:
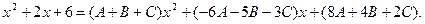
Сравнивая коэффициенты при одинаковых степенях x, получаем систему уравнений
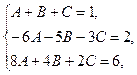
из которой найдем 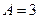 ,
, 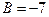 ,
, 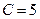 .
.
Итак, разложение рациональной дроби на простейшие имеет вид
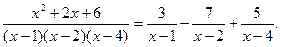
Таким образом,
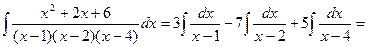
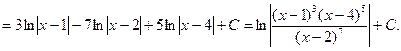
Дата добавления: 2020-10-25; просмотров: 517;











