Геометрическое представление комплексных чисел
Известно, что каждому действительному числу соответствует единственная точка числовой прямой. Аналогично каждому комплексному числу можно поставить во взаимно однозначное соответствие точку плоскости с координатами (a,b). Числа вида (а,0) изображаются точками оси ОХ, поэтому ось ОХ называется действительной осью, а числа вида (0,а) изображаются точками оси ОУ, поэтому ось ОУ называется мнимой осью. Однако точку плоскости можно задать либо парой декартовых координат, либо полярными координатами. Таким образом, каждому комплексному числу можно поставить в соответствие вектор, выходящий из начала координат и заканчивающийся в точке с координатами (a,b). Но вектор может быть задан длиной и величиной угла, составленного с положительным направлением оси ОХ.
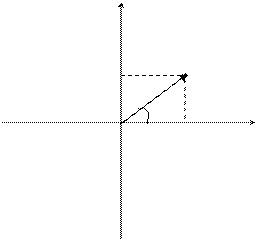 A
A
b (a,b)
a
Тригонометрическая форма записи
Комплексного числа
Определение. Длина вектора, соединяющего начало координат с точкой (a,b), называется модулем комплексного числа a=a+bi, угол, который этот вектор составляет с положительным направлением оси ОХ, называется аргументом комплексного числа a=a+bi. Обозначение
½a½=r=Öa2+b2
arg a=j,
sin j= 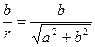
cos j= 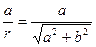 .
.
Таким образом, всякое комплексное число можно записать в виде
a=a+bi= 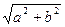 (
( 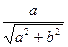 +
+ 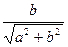 i)=r(cosj+isinj), то есть
i)=r(cosj+isinj), то есть
a= r(cosj+isinj).
Такая форма записи называется тригонометрической формой записи комплексного числа. Рассмотрим действия над комплексными числами, записанными в тригонометрической форме.
Равенство
Пусть a=r(cosj+isinj), b=r1(cosj1+isinj1), тогда
a=bÛ 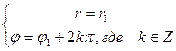
умножение
Пусть a=r(cosj+isinj), b=r1(cosj1+isinj1), тогда
ab=rr1(cosjcosj1+cosjisinj1+isinjcosj1+i2sinjsinj1)=rr1(cosjcosj1- sinjsinj1 +cosjisinj1+isinjcosj1)=rr1(cos(j+j1)+isin(j+j1)). Таким образом
½ab½=½a½½b½
arg(ab)=arga+argb.
Это правило можно применить для нахождения произведения n сомножителей, то есть
½a1a2…an½=½a1 ½½a2½…½an½
arg(a1a2…an)=arga1 +arga2 +…+argan
доказать самостоятельно методом математической индукции.
возведение в степень
Докажем формулу, известную как формула Муавра,
"aÎC"nÎN(an =rn (cosnj+isinnj)).
Доказательство проведем методом математической индукции. Если n=1, то формула верна. Предположим, что формула справедлива для n=k, то есть
(ak =rk (coskj+isinkj)), и докажем для n=k+1
an = ak+1=aka=rk (coskj+isinkj)r(cosj+isinj)= rkr (cos(kj+j)+isin(kj+j))=
=rk+1(cos((k+1)j)+isin((k+1)j))= rn (cosnj+isinnj), то есть формула верна, следовательно, она верна для любого натурального числа n.
В качестве упражнения доказать, что формулу Муавра можно обобщить на случай целого показателя.
деление
Пусть a=r(cosj+isinj), b=r1(cosj1+isinj1), тогда
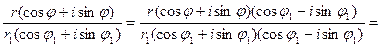
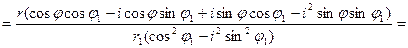
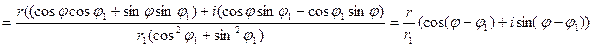 .
.
Таким образом,
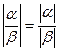
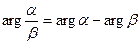 .
.
извлечение корня
Обозначим 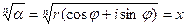 Û xn=a. Будем искать х исходя из условия, что хÎС, то есть х=r1(cosj1+isinj1), тогда хn =r1n (cosnj1+isinnj1).
Û xn=a. Будем искать х исходя из условия, что хÎС, то есть х=r1(cosj1+isinj1), тогда хn =r1n (cosnj1+isinnj1).
xn=a Û r1n (cosnj1+isinnj1)= r(cosj+isinj) Û Û 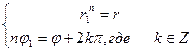 Û
Û 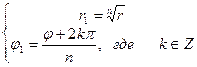 ,
,
Получили формулу для извлечения корня n-ой степени из произвольного комплексного числа:
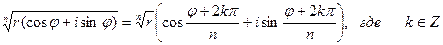 .
.
Легко доказать, что существует ровно n значений корня n-ой степени из комплексного числа, которые вычисляются по формуле
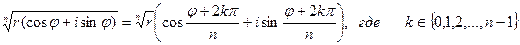 (1)
(1)
Для этого достаточно показать, что совпадают два множества:
А= 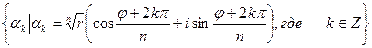 и
и
В= 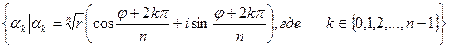 .
.
Очевидно, ВÌА, так как {0,1,2,…,n-1}ÌZ. Докажем обратное включение. Пусть amÎAÛam= 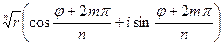 , где mÎZ. По теореме о делении с остатком "mÎZ"nÎZ$!q, rÎZ (m=nq+r Ù0£r<n), тогда "amÎA, имеем am=
, где mÎZ. По теореме о делении с остатком "mÎZ"nÎZ$!q, rÎZ (m=nq+r Ù0£r<n), тогда "amÎA, имеем am= 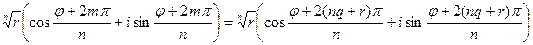 =
=
= 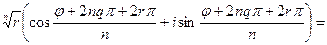
= 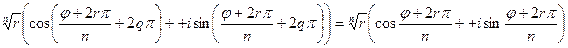 , где 0£r<n, следовательно, amÎВ, таким образом, А ÌВ. Оба включения доказаны, следовательно, А=В. Осталось доказать, что все элементы множества В различны. Действительно, если предположить противное, то есть akÎB, amÎB,
, где 0£r<n, следовательно, amÎВ, таким образом, А ÌВ. Оба включения доказаны, следовательно, А=В. Осталось доказать, что все элементы множества В различны. Действительно, если предположить противное, то есть akÎB, amÎB,
ak=amÛ 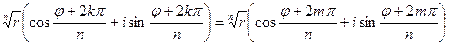 Û Û
Û Û 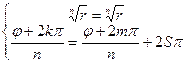 , где k.mÎ{0.1.2…..n-1}, SÎz, k¹m
, где k.mÎ{0.1.2…..n-1}, SÎz, k¹m
В качестве 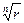 берется только арифметическое значение корня, а из второго равенства получаем
берется только арифметическое значение корня, а из второго равенства получаем
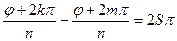 Û
Û 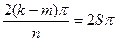 Û
Û 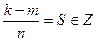 . Так как 0£k<n Ù 0£m<n, тогда ïk-mï<n, следовательно,
. Так как 0£k<n Ù 0£m<n, тогда ïk-mï<n, следовательно, 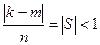 ÛS=0Ûk=m – получили противоречие. Таким образом, мы доказали, что все корни n-ой степени из произвольного комплексного числа a исчерпываются числами множества В, а это множество содержит ровно n различных элементов.
ÛS=0Ûk=m – получили противоречие. Таким образом, мы доказали, что все корни n-ой степени из произвольного комплексного числа a исчерпываются числами множества В, а это множество содержит ровно n различных элементов.
Пример. Вычислить 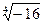 . Переведем число -16 в тригонометрическую форму. Для этого найдем его модуль и аргумент
. Переведем число -16 в тригонометрическую форму. Для этого найдем его модуль и аргумент
r=ï-16ï= 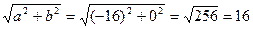
cosj= 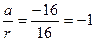
sinj 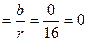 , следовательно, j=π, то есть -16=16(сos π + isin π), тогда, по формуле (1), имеем
, следовательно, j=π, то есть -16=16(сos π + isin π), тогда, по формуле (1), имеем 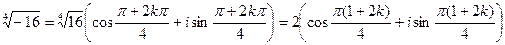 , k=0,1,2,3.
, k=0,1,2,3.
При k=0 получим a0=2(сos 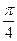 +isin
+isin 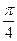 )=2(
)=2( 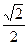 +i
+i 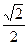 )=
)= 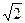 +i
+i 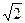 .
.
При k=1 получим a1=2(сos 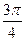 +isin
+isin 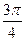 )=2(-
)=2(- 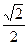 +i
+i 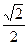 )=-
)=- 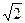 +i
+i 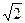 .
.
При k=2 получим a2=2(сos 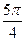 +isin
+isin 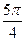 )=2(-
)=2(- 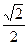 -i
-i 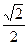 )=-
)=- 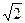 -i
-i 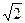 .
.
При k=3 получим a3=2(сos 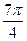 +isin
+isin 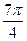 )=2(
)=2( 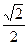 -i
-i 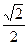 )=
)= 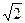 -i
-i 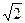 .
.
Из равенства (1) легко понять, какой геометрический смысл имеет значение 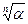 при a¹0. Так как модуль всех чисел ak общий, то точки, изображающие эти числа, лежат на окружности радиуса
при a¹0. Так как модуль всех чисел ak общий, то точки, изображающие эти числа, лежат на окружности радиуса 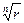 с центром в начале координат. Аргументы ak и ak+1 отличаются на
с центром в начале координат. Аргументы ak и ak+1 отличаются на 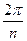 , следовательно, точки, изображающие корни n-ой степени из комплексного числа a, лежат в вершинах правильного n-угольника, вписанного в окружность радиуса
, следовательно, точки, изображающие корни n-ой степени из комплексного числа a, лежат в вершинах правильного n-угольника, вписанного в окружность радиуса 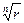 с центром в начале координат, причем положение вершин определяется однозначно, так как одна из вершин изображает число a0 с аргументом
с центром в начале координат, причем положение вершин определяется однозначно, так как одна из вершин изображает число a0 с аргументом 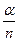 .
.
Замечание 1. В курсе теории функции комплексной переменной путем разложения функции комплексной переменной в степенной ряд, доказывается формула Эйлера:
eij=cosj+isinj,
откуда получаем показательную форму записи комплексного числа:
a=r eij.
Замечание 2. Следует обратить внимание на соотношение между вновь введенными понятиями модуля и аргумента комплексного числа с известными свойствами действительных чисел. Оказывается, понятие модуля комплексного числа является обобщением понятия модуля действительного числа, а понятие аргумента комплексного числа – обобщением понятия знака действительного числа. В самом деле, если a=a+biÎÂÛb=0Ùa=a Þ r= 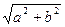 =ïaï. И если a=a+biÎÂÛb=0Ù cosj=
=ïaï. И если a=a+biÎÂÛb=0Ù cosj= 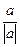 =ï1ïÙsinj=0, поэтому аргумент равен 2kπ для положительных чисел и π+2лπ для отрицательных.
=ï1ïÙsinj=0, поэтому аргумент равен 2kπ для положительных чисел и π+2лπ для отрицательных.
Дата добавления: 2020-10-25; просмотров: 4764;











