Вложение области целостности в поле

Определение. Кольцо К называется областью целостности, если из ab=0 в К следует a=0 или b=0.

Примеры. 1. Кольцо целых чисел z - область целостности.

2. Поле Р - область целостности.

Определение. Будем говорить, что кольцо К вложимо в некоторое поле Р, если существует гомоморфизм К в Р, являющийся инъекцией.

теорема. Для того, чтобы кольцо К было вложимо в некоторое поле Р, необходимо и достаточно, чтобы К было областью целостности и коммутативно.

Доказательство

I. Необходимость. Пусть кольцо К вложимо в некоторое поле Р, тогда существует инъективный гомоморфизм ¦ кольца К в поле Р.

а) докажем, что умножение в К – коммутативно. Допустим, что для не которых a,bÎK имеет место: ab¹ba, тогда поскольку ¦ инъекция, то ¦(ab)¹¦(ba), но ¦(a), ¦(b), ¦(ab), ¦(ba)ÎP и умножение в Р по определению поля коммутативно. 0тсюда ¦(ab)=¦(a)צ(b)=¦(b)צ(a)=¦(ba), ибо ¦ - гомоморфизм из К в Р. Полученное противоречие доказывает коммутативность умножения в К;

б) докажем, что К - область целостности. Пусть а,bÎК и аb=0. Тогда так как ¦ - гомоморфизм, то ¦(ab)=¦(a)צ(b)=¦(0)=0_P. Предположим, что ¦(a)¹0_P и ¦(b)¹0_Р, тогда в поле Р для них существуют обратные элементы. Пусть tÎP – обратный для ¦(а), тогда получим t×(¦(a)צ(b))=(tצ(a))צ(b)=¦(b) и t×(¦(a)צ(b))=t×0_P=0_P. Следовательно, либо ¦(а)=0_P, либо ¦(b)=0_P, откуда получаем, что а=0 или b=0. Таким образом, мы доказали, что К - область целостности.

II. Достаточность. Пусть К - коммутативное кольцо, являющееся областью целостности. Для доказательства нужно построить поле Р и бинарное отношение j между К и Р, которое являлось бы функцией, отображением, инъекцией и было бы гомоморфизмом кольца К в поле Р.

1. Построим поле Р .

а) Рассмотрим множество S=K´(K\{0}) и введем на нем отношение s: ((a,b),(c,d))Îs Û ad=bc (а,сÎК, b,dÎK\{0}). В дальнейшем вместо (a,b) будем писать .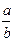

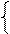
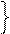Покажем, что s - эквивалентность. Очевидно, что ( 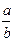, 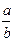)Îs для всяких aÎК и bÎK\{0}, ибо ab=ba, в силу коммутативности умножения в К. Итак, s - рефлексивно. Далее, если ( 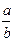, 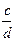)Îs, то ad=bc. Так как умножение в К - коммутативно, имеем da=cb и, следовательно, ( 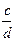, 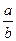)Îs, то есть s симметрично. Пусть ( 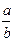, 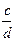)Îs и ( 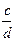, 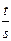)Îs, где a, c, tÎK; b,d, sÎK\{0}, тогда ad=bc и cа=dt. Умножив первое равенство на а, а второе на b, получим ads=bcs и bcs=bdt, то есть ads=bdt или asd=btd. отсюда asd-btd=(as-bt)d=0 и, учитывая, что d¹0, получим as-bt=0 или as=bt и, значит, ( 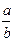, 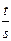)Îs. То есть отношение s - транзитивно и, следовательно, s - эквивалентность. Это отношение разбивает множество S на классы эквивалентности. Рассмотрим множество P=S/s= 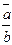½aÎK, bÎK\{0}

б) Введем на множестве Р действия сложения и умножения по следующим правилам: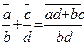

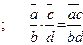
Прежде всего, покажем, что определения корректны, то есть сложение и умножение не зависят от выбора представителей. Доказательство проведем для сложения, для умножения доказать самостоятельно.

Нужно доказать, что если мы имеем класс 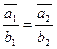и класс 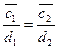, то есть классы, заданные различными представителями, то их суммы совпадают вне зависимости от того, по каким представителям проводилась операция сложения. Таким образом, нужно показать, что

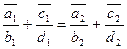или

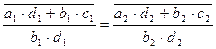
Для этого нужно показать, что

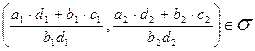или

b₂×d₂×(a₁×d₁+b₁×c₁)=b₁×d₁×(a₂×d₂+b₂×c₂).

Имеем:

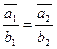и 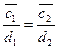, то есть a₁×b₂=b₁×a₂ и c₁×d₂=d₁×c₂, отсюда получаем b₂×d₂×(a₁×d₁+b₁×c₁)= b₂×d₂×a₁×d₁+ b₂×d₂×b₁×c₁= b₁×d₁×a₂×d₂+b₂×d₁×b₁×c₂= b₁×d₁ ×(a₂×d₂+b₂××c₂),

что и требовалось доказать.

Проверим некоторые свойства из определения поля, а именно, обратимость умножения и коммутативность сложения, остальные проверяются аналогично.

Пусть 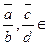Р и 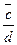¹0 (b,dÎK\{0}). Из 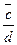¹0= 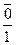следует, что c×l¹d×0, то есть с¹0. Рассмотрим элемент x= 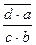Так как с¹0 и b¹0 и К - область целостности, то c×b¹0 и класс 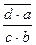ÎR. Имеем 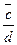×x= 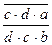=t. С другой стороны, b(cda)=(dcb)a и, значит, 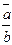= 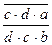, то есть x - решение уравнения × 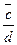×x= 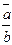, следовательно, умножение в Р обратимо (при условии, что делитель отличен от нуля).

Пусть 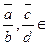Р, тогда 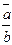+ 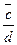= = 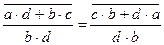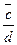+ 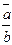, то есть сложение в Р коммутативно. Итак, Р - поле.

2. Докажем, что существует гомоморфизм из К в Р, являющийся инъекцией. Определим бинарное отношение j между множествами К и Р такое что j(а)= 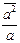(аÎК, a¹0) и j(0)= 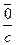, где с - ненулевой элемент К. Указанное отношение является функцией и отображением, ибо для каждого аÎК однозначно определена пара (a²,а) по определению декартова произведения, и так как s - эквивалентность, то каждая пара находится в некотором классе S, но не может находиться в двух классах одновременно. Покажем, что j - инъекция. Пусть a₁¹0, а₂¹0, а₁¹ а₂, но j(а₁)=j(а₂), то есть

,

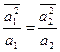отсюда 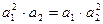, тогда а₁а₂(а₁-а₂)=0, но К - область целостности, значит, a₁ –a₂=0 и а₁=а₂, что невозможно.

Пусть а₁=0, a₂¹0. Предположим, что j(а₁)=j(а₂), тогда 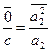(с¹0), то есть 0= 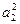и так как К - область целостности, то из a₂×a₂=0 следует a₂=0, что противоречит условию. Покажем, что j - гомоморфизм колец. Действительно,

а) j(a×b)= 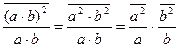=j(a)×j(b), если a¹0, b¹0;

b) если а=0, b¹0, тогда j(а×b)=j(0)=0_P, j(а)= 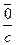, где (c¹0), j(b)= 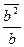. Тогда j(a)×j(b)= 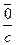× 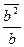= =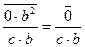0_P, то есть и в этом случае j(а×b)= j(a)×j(b).

Самостоятельно проверить случай a=0, b=0 и показать, что j сохраняет операцию сложения. Таким образом, j - инъективный гомоморфизм кольца K в поле Р, и теорема доказана.