КЛАССЫ ВЫЧЕТОВ ПО ИДЕАЛУ КОЛЬЦА

Пусть J - некоторый идеал кольца к. Элементы а, b кольца к называются сравнимыми по идеалу J, если a- b ÎJ и обозначаются aº b (J).

Упражнения. Показать, что отношение сравнения по идеалу J в кольце К (на множестве К) является отношением эквивалентности.

Определение. Классы эквивалентности отношения сравнения по идеалу J в кольце К называются классами вычетов по идеалу J, или смежными классами кольца К по идеалу J.

Рассмотрим основные свойства сравнений по идеалу:

1. Из aºb(J) и cºd(J) следует, что a±сºb±d(J).

Доказательство. В самом деле, если (a- b)ÎJ и (с-d)ÎJ, то (a+c)-(b+d)ÎJ и (a-c)-(b-d)ÎJ. Следовательно, a±сºb±d(J).

2. Из aºb(J) и сÎК следует aсºbс(J), сaºсb(J).

Доказательство. Множество J устойчиво относительно умножения на элементы кольца. Следовательно, для любого элемента с кольца J, так как a-bÎJ, то и aс- bсÎJ и сa-сbÎJ.

3. Из aºb(J) следует, что na=nb(J), где nÎZ.

Доказательство. Так как a- b ÎJ, то nа- nb = n(а- b)Î J.

4. Из aºb(J) и сºd(J) следует, что aсºbd(J).

Доказательство. В самом деле, если (a-b)ÎJ и (c-d)ÎJ, то, в силу устойчивости идеала J относительно сложения и умножения на элементы кольца, имеем ac-bd =ac-bc+bc-bd=(a-b)c+b(c-d)ÎJ.

Определение. Множество всех классов вычетов называется фактор-множеством К по идеалу J, что обозначается к/J.

Класс вычетов, содержащий элемент а кольца к, будем обозначать .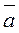

Как следует из свойств 1-4, на фактор-множестве к/J можно определить операции таким образом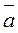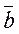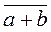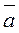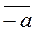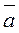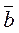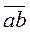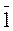: + = , - = , × = , =J для любых элементов 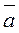и и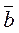з K/J. Такое определение операций в K/J является корректным, так как не зависит от выбора а и b в смежных классах 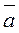и 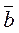соответственно.

Можно доказать, что K/J=(K/J,+,×, 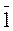) является кольцом, его называют фактор-кольцом кольца К по идеалу J.