Дискретизация непрерывных сигналов

Передача информации на значительные расстояния по дискретным (цифровым) каналам связи, широкое использование микропроцессоров и ЦВМ для обработки информации определяет необходимость преобразование непрерывных аналоговых сигналов в цифровую форму, т. е. их дискретизацию.

Важной задачей при таком преобразовании является выбор интервала дискретизации, поскольку при слишком малом интервале дискретизации может оказаться неоправданно большое число точек отсчета полученного дискретного сигнала и наоборот, при большом интервале дискретизации может иметь место потеря информации.

Поэтому при дискретизации непрерывных сигналов ставится задача определить такой интервал дискретизации (т. е. преобразовать непрерывный сигнал в последовательность дискретных значений, взятых через определенный интервал времени – интервал дискретизации (Δt=Δ), при котором погрешность восстановления исходного непрерывного сигнала по дискретным отсчетам (при последующей обработке) не будет превышать заданного значения.

Для решения этой задачи необходимо получить соотношения, связывающие величину интервала дискретизации Δ с погрешностью восстановления σ исходного сигнала при последующей обработке.

Эти соотношения наиболее просто получаются на основе рассмотрения спектральных свойств непрерывного и дискретного сигналов.

Если какой либо сигнал x(t) представлен в виде суммы гармонических составляющих с различными амплитудами и частотами, то говорят, что осуществляется спектральное разложение этого сигнала [9].

Сумма отдельных гармонических компонент периодического сигнала образуют его спектр

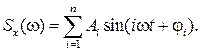(4.44)

Спектральное представление непрерывного неслучайного сигнала x(t) можно получить, используя разложение в ряд Фурье. При этом сигнал x(t) и его спектральная плотность S_x(ω) взаимнооднозначны и связаны прямым и обратным преобразованием Фурье

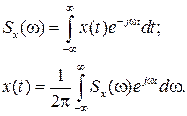(4.45)

Аналогичные соотношения имеют место и для спектральной плотности мощности 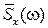случайного сигнала x(t)

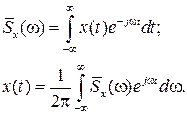(4.46)

Пусть x(t) – непрерывный сигнал, который имеет спектр или спектральную плотность, или спектральную плотность мощности S_x(ω), ограниченные частотой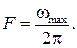

Тогда спектр (спектральная плотность) дискретизированного сигнала S_xд(f) представляет собой результат суммирования бесконечного числа "копий" спектра исходного сигнала, которые располагаются на оси частот через равные промежутки 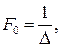равные значению частоты дискретизации F₀, т. е.

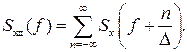(4.47)

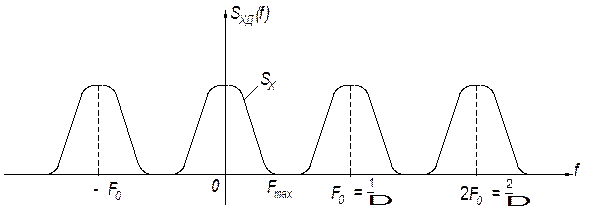
Рис.4.6. Спектральные характеристики дискретного сигнала

Если F_max – верхняя граничная частота в спектре исходного сигнала x(t), то при 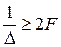отдельные лепестки спектральной диаграммы дискретизированного сигнала перестают накладываться друг на друга. Поэтому такой непрерывный сигнал, подвергнутый импульсной дискретизации может быть восстановлен с помощью идеального фильтра нижних частот, если на его вход подать импульсную последовательность вида (4.47).

Наибольшее значение интервала дискретизации составит при этом величину

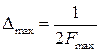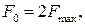или (4.48)

что соответствует известной теореме Котельникова.

Если интервал дискретизации будет больше 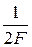, то смещенные спектры будут перекрываться и точное восстановление исходного сигнала x(t) оказывается невозможным. В этом случае необходимо учитывать связь между интервалом дискретизации и погрешностью восстановления.

Здесь возможно несколько характерных случаев

1. Если сигнал x(t) детерминированный и имеет спектр S_x(f) и задана допустимая погрешность восстановления ε_max, то необходимая частота дискретизации 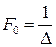может быть определена не явно из соотношения

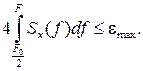(4.49)

2. При случайном входном сигнале x(t) и заданном максимальном значении среднеквадратической погрешности восстановления σ_max, то необходимая частота дискретизации 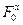, при которой может быть обеспечена требуемая точность восстановления, выбирается из условия

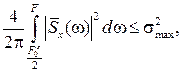(4.50)

где 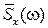– спектральная плотность мощности случайного сигнала x(t).

Реальные сигналы часто имеют ветви спектральных характеристик большой протяженности с убывающей интенсивностью. Если частоту дискретизации выбирать из полученных ранее зависимостей, то она окажется чрезвычайно высокой.

Как же в этом случае поступить?

Если спектр сигнала имеет бесконечную протяженность (рис. 4.7), то частоту дискретизации выбирают пропорционально F_э, где F_э – эффективная ширина спектра, выбираемая из условия

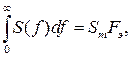(4.51)

т. е. в предположении, что площадь, ограниченная кривой S(f), равна площади прямоугольника с высотой S_m и основанием F_э.

Эффективная ширина спектра случайного сигнала F_э связана с интервалом корреляции τ₀ соотношениями

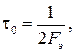
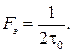(4.52)

Если дискретизируемый сигнал x(t) представляет собой стационарный случайный процесс с дисперсией 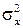и корреляционной функции вида

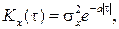(4.53)

то спектральная плотность мощности этого сигнала будет иметь вид

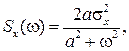(4.54)

где 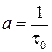- величина, обратная интервалу корреляции.

Тогда

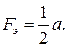(4.55)

При этом дисперсия γ² относительной приведенной погрешности дискретизации для нормального закона распределения случайного сигнала x(t) определяется соотношением

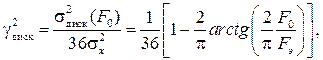(4.56)

где 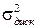– дисперсия погрешности дискретизации.

Рис. 4.7. Выбор эффективной частоты спектра сигнала

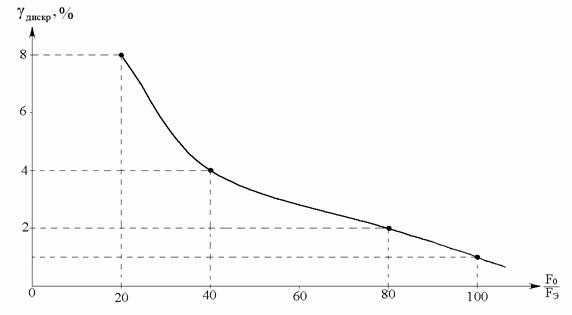
Рис. 4.8. Связь относительной погрешности дискретизации с частотой дискретизации

Для равномерного закона распределения случайного сигнала x(t) соотношение (4.56) принимает вид

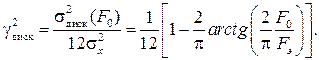(4.57)

Полученные соотношения позволяют определить частоту дискретизации F₀ при известных характеристиках случайного сигнала x(t) с допустимой погрешностью γ_диск.

Связь среднеквадратического значения относительной приведенной погрешности дискретизации с частотой дискретизации F₀ можно проиллюстрировать следующим графиком (рис. 4.8).

Расчеты показывают, что γ_диск=10% достигается при F₀=11F_э, γ=1% - при F₀=100F_э.

Так как при восстановлении дискретизированного сигнала реальный фильтр будет отличаться от идеального, то на практике отношение частот 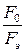необходимо выбирать больше расчетного.