Объемы земляных масс. Определение объема отсеков земляного полотна

Определение объема отсеков земляного полотна. Необходимость в подсчете объемов земляных масс возникла задолго до появления железных дорог в связи со строительством дамб и каналов. Искусственные поверхности этих сооружений обычно делали плоскими; плоскостями условно заменяли при расчетах и земную поверхность.

Поэтому любой участок такого сооружения, выделенный между двумя параллельными сечениями, нормальными к продольной оси, имел в общем виде форму призматоида — многогранника с параллельными торцовыми плоскостями (основаниями), боковые грани которого являются трапециями или треугольниками (рис. 3.12, а).

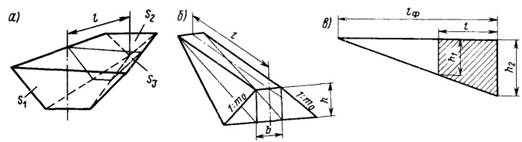
Рис. 3.12. Определение объемов: а — призматоида; б — трапецеидального клина; в — усеченного клина

Объем призматоида определяют по формуле

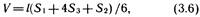
где S₁, S₂— площади торцовых сечений призматоида; S3 — площадь сечения, одинаково удаленного от торцов.

Эта формула успешно использовалась для расчета объемов дамб и каналов, поскольку для них типична однозначность высоты и глубины, благодаря чему практически по всей длине на любом участке сооружения можно было реально вычислить три значения площадей S.

Когда появились железные дороги, в их земляном полотне нашли известное сходство с прежними грунтовыми сооружениями и воспользовались формулой (3.6), которая была приведена к удобному для расчета виду с учетом трапецеидального очертания поперечников насыпей и выемок. Расчетные формулы предлагались многими исследователями.

По этим формулам были составлены таблицы, облегчающие подсчет объемов, но он все еще остается довольно громоздким. Для земляного полотна типична знакопеременность высотного размера с более или менее частыми переходами через нуль.

Высота насыпей и глубина выемок в пересеченной местности меняются практически непрерывно, а поперечные сечения остаются в геометрическом отношении сравнительно однородными. Для этих условий более представительной и общей фигурой является трапецеидальный клин (рис. 3.12, б).

Объем такого клина подсчитывают как сумму объема треугольной призмы с высотой b и площадью основания hl/2 и объемов двух треугольных пирамид с основанием m_оhh/2 и высотой I. Отсюда

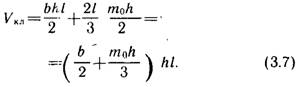
Клинообразную форму может иметь объем элемента земляного полотна на начальном участке насыпи или выемки. Для подсчета объема любого другого отрезка или отсека земляного полотна, ограниченного сечениями с высотами h₂ и h₁, можно воспользоваться приемом усечения клина с фиктивной длиной L_ф (рис. 3.12, в). При этом формулу (3.7) нужно применить дважды: сначала найти объем полного клина с длиной L_ф, а затем объем отсекаемой части с длиной L_ф— _L. Опуская несложные промежуточные выкладки, получим

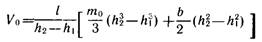
В этом выражении возможно сокращение на h₂ — h₁, что дает:

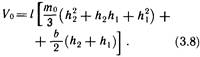
Вводя в прямые скобки равное нулю выражение h₂h₁ — h₂h₁, получим дополнительное алгоритмическое упрощение:

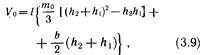
позволяющее оперировать с суммой и произведением высот h₁ и h₂ концевых сечений отсека. С помощью микрокалькулятора вычисления по формуле (3.8) выполняются цепочкой:

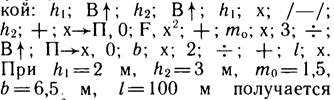
получается 2775 м³, на что затрачивается около 1 мин. Это во много раз меньше времени, потребного для подготовки исходных данных, снимаемых с продольного профиля.

Поэтому микрокалькулятор удобно применять попутно с систематизацией информации в форме той или иной ведомости. Многократное повторение расчетом по программе практически требует лишь времени на ввод данных и запись результатов. Пока ведется счет, можно заниматься с ведомостью.

Формула (3.9) представляет собой простейшую математическую модель расчета объема отсека земляного полотна, которая пока не учитывает наличия сливной призмы и кюветов в выемках, а также влияния косогорности.

Площадь поперечного сечения сливной призмы (рис. 3.13), численно равную ее объему на длине 1 м, при нормативных размерах определяют по формулам: для однопутных линий 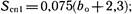ДЛЯ двухпутных линий .

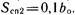Рис. 3.13. Размеры сливной призмы однопутных (а) и двухпутных (б) дорог

В выемках площадь S_cn не входит в поперечник разрабатываемой фигуры, но необходимо принять во внимание наличие кюветов. Поэтому в расчет вводят разность S_KB— S_СП, где S_КВ — площадь двух кюветов. При нормативных размерах, установленных для наиболее распространенных грунтовых условий, S_KB = 1,56 м2. Дополнительный объем получается умножением соответствующей площади на длину L, как и в основной формуле (3.9).

Косогорность влечет за собой увеличение площадей поперечного сечения отсеков земляного полотна, что видно из рис. 3.14, где дополнительная площадь показана штриховкой. Эту площадь можно вычислить как разность площадей треугольников ОАВ и OCD.

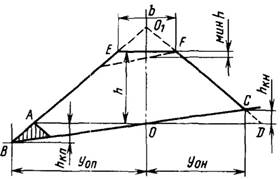
Рис. 3.14. Определение дополнительной площадки поперечного сечения на косогорном участке

Основание каждого из этих треугольников равно b/2 + m_oh. Высота получается при делении на тк абсцисс точек нулевых работ, которые можно найти по формуле (3.4). Для треугольника ОАВ h_кп = (h + b/2m_о)m_o/(m_K — m₀), для треугольника OCD h_KH = (h + b/2m₀)m_о/(m_k + m_o) Разность площадей

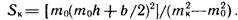
Если развернуть выражение квадрата суммы и вынести за скобки m_о, то оказывается, что дополнительная площадь S_К прямо пропорциональна сумме двух площадей, одна из которых представляет собой площадь b²/4m₀ треугольника ЕО₁Е (см. рис. 3.13), другая — площадь h(b + m₀h) трапеции AEFD. Следовательно, S_K вычисляется как некоторая доля площади треугольника AO₁D, а коэффициент пропорциональности К_пк является отношением показателей крутизны откоса и косогора:

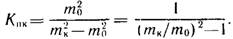
Если теперь перейти к рассмотрению откоса, в сечениях которого высоты изменяются от h₁ до h₂, то площадь b₂/4m_o останется неизменной в любом сечении, а площадь трапеции нужно взять в некотором расчетном значении, умножение которого на длину отсека давало бы его объем V_o. Эту площадь определяют при вычислении основного объема. Она входит в формулу (3.9), которая в развернутой записи приобретает вид

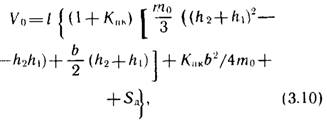
где S_д — добавочная площадь отсека, введением которой учитывают различные дополнения поперечника, в том числе за счет сливной призмы и кюветов, уположения откосов, наличия присыпных берм и т. д.

Обычно влиянием косогорности пренебрегают при 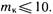. Это допустимо лишь при небольших высотах насыпей и глубинах выемок. Целесообразно всегда ориентироваться по результатам расчетов. На участках с горизонтальным основанием следует принимать m_k = 50... ...100; это само собой исключит влияние косогорности. На косогорах крутизной 1:3 и более в пределах основания насыпи производят нарезку уступов шириной 1...4 м и высотой до 2 м (рис. 3.15).

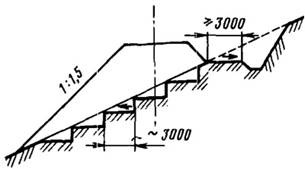
Рис. 3.15. Нарезка основания уступами на косогорах круче 1:5

Это приводит к дополнительному существенному увеличению объема грунта в насыпи, определяемому в зависимости от принятых размеров и числа уступов. Однако в практике железнодорожного строительства подобные случаи встречаются довольно редко. Земляное полотно при этом проектируют индивидуально.

При сложных очертаниях основания, например, когда насыпь делают в виде присыпки к скальной стене, подмытому берегу и т. д., поперечник приводят к форме произвольного многоугольника; площади определяют, разбивая многоугольник на простые фигуры. Если предварительно можно найти координаты вершинных точек многоугольника, то площадь определяют по координатам способом, известным из геодезии.

Этот метод весьма громоздок при использовании обычных средств вычисления, но все трудности снимаются при расчете на ЭВМ. В результате удается определить объемы отсеков с произвольным очертанием концевых сечений, если только эти отсеки имеют форму призматоида.

Для учета недобора в процессе допланировочной разработки выемок и запаса на осадку, планировку и потери грунта в насыпях объемы отсеков выемок принимают с понижающим коэффициентом 0,9; насыпей— с коэффициентом 1,05...1,1, включая потери при транспортировании, принимаемые в соответствии с нормами 0,5...1 % в зависимости от вида транспорта и рассстояния перевозки.

Объемы по отсекам в совокупности могут дать представление о потребности в разработке и укладке грунта на участке, если их представить в форме диаграммы или кривой. Диаграмму объемов земляных масс по отсекам строят в масштабе расстояний профиля (рис. 3,16, б).

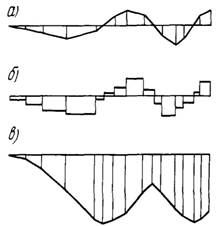
Рис. 3.16. Графическое изображение изменения объемов земляных масс на участке: а продольный профиль; б —диаграмма объемов; в - кумулятивная кривая

Объемы грунта показывают столбиками в произвольном масштабе и откладывают на участках выемок и насыпей в разные стороны от оси отсчета, например, для выемок — вверх (положительные значения), для насыпей—вниз (отрицательные значения). По виду диаграммы можно судить о том, на каких участках профиля сконцентрированы большие, на каких — меньшие объемы земляных работ.

Если прирост объемов в пределах каждого отсека выразить наклонной прямой, а затем просуммировать нарастающим итогом с учетом разных знаков для насыпей и выемок, получим кумулятивную кривую уравновешивания (рис. 3.16 в), которая позволяет судить о балансе земляных масс на участке в предположении, что грунт из выемок полностью перевозится в насыпи. Если кривая уходит в общем кверху от оси отсчета, это указывает на избыток грунта на участке, если книзу,— на недостаток.

На участке, где кривая дважды пересекает линию отсчета, возможен баланс земляных масс, т. е. грунт из выемок полностью размещается в насыпях. Кривую уравновешивания используют при решении задачи о целесообразном распределении земляных масс. Однако такие расчеты правомерны, если принимаются во внимание физические объемы грунта в отсеках, а не просто объемы геометрических фигур, образованные земляным полотном выше или ниже земной поверхности.