КОС с дискретным датчиком

В дискретном датчике преобразование непрерывного сигнала в дискретный и соответствующее квантование по уровню происходит внутри самого датчика, сигнал на его выходе представляется уже в цифровом виде. Поэтому мы можем рассматривать дискретный датчик как АЦП, понимая под АЦП здесь любое устройство, осуществляющее квантование по уровню. Следовательно, в случае дискретного датчика КОС также описывается схемой, представленной на рис. 7.

АЦП и его характеристики

Обычно АЦП рассматривают как статический элемент, то есть предполагают, что запаздывание сигналов, проходящих через него, очень мало. Однако в высокоскоростных системах приходится учитывать конечность времени преобразования в АЦП непрерывного сигнала в соответствующий цифровой код.

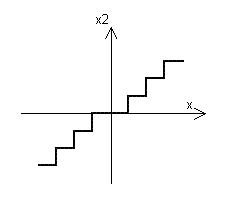
Реальный АЦП имеет следующую характеристику (рис. 8):

Рис. 8.

То есть он является нелинейным элементом. Горизонтальный размер ступеньки на характеристике называется ценой младшего разряда АЦП ( 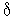). Чем меньше цена младшего разряда, тем большее число разрядов двоичного числа необходимо для представления преобразованного значения при одном и том же диапазоне его изменения. На практике цена младшего разряда выбирается исходя из максимально допустимой ошибки (они должны быть примерно равны): .

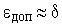Наличие нелинейного элемента в цепи обратной связи будет приводить к возникновению автоколебаний, амплитуда которых сравнима с ценой младшего разряда АЦП. Однако колебания могут демпфироваться силами трения в опорах, которые играют роль нелинейного элемента с зоной нечувствительности. На практике, для того, чтобы уйти от эффекта автоколебаний, увеличивают разрядность АЦП на 2-3 разряда по сравнению с той, которая необходима для обеспечения требуемой точности системы. В расчетах часто используется линеаризованную статическую характеристику АЦП, представляя его усилительным звеном с коэффициентом усиления .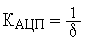

Подобная линеаризация оправдана при условии большого количества разрядов АЦП и малого значения 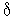.Влияние нелинейных факторов на работу скорректированной системы оценивается отдельно.