ПРОСТЕЙШИЕ СВОЙСТВА ГРУПП
Пусть G - группа, а, b - произвольные элементы группы G.
1. (а´b)-1=b-1´а-1
Доказательство. Воспользуемся определением обратного элемента. Покажем, что (а´b)´(b-1´а-1)= (b-1´а-1) ´(а´b)=е. (*)
Тогда по определению это будет означать, что элемент b-1´а-1 является обратным для а´b, то есть (а´b)-1= b-1´а-1. Итак, докажем (*):
(а´b)´(b-1´а-1)= а´(b´b-1)´а-1=(а´e)´а-1=а´а-1=e.
2. (a-1)-1=a.
3. Если а´b=а´с, то b=с. Если b´а=c´а, то b=c.
ГРУППЫ СИММЕТРИИ
 В дальнейшем, как это принято в геометрии, под преобразованием множества М будем понимать биекцию М на себя (взаимнооднозначное отображение М на М). Так, если f - преобразование плоскости, то, во-первых, различные точки плоскости переходят в различные точки плоскости при отображении f, и, во-вторых, f - отображение плоскости на всю эту плоскость, то есть для любой точки В найдется точка A, переходящая в точку В при отображении f. Примерами преобразований служат любые перемещения, любая гомотетия, подобие. Преобразования конечного множества называются подстановками. Существуют различные способы задания подстановок: схемой, матрицей, графом. Матричный способ прост и удобен, а изображение подстановки c помощью графа обладает хорошей наглядностью. Примеры задания подстановок:
В дальнейшем, как это принято в геометрии, под преобразованием множества М будем понимать биекцию М на себя (взаимнооднозначное отображение М на М). Так, если f - преобразование плоскости, то, во-первых, различные точки плоскости переходят в различные точки плоскости при отображении f, и, во-вторых, f - отображение плоскости на всю эту плоскость, то есть для любой точки В найдется точка A, переходящая в точку В при отображении f. Примерами преобразований служат любые перемещения, любая гомотетия, подобие. Преобразования конечного множества называются подстановками. Существуют различные способы задания подстановок: схемой, матрицей, графом. Матричный способ прост и удобен, а изображение подстановки c помощью графа обладает хорошей наглядностью. Примеры задания подстановок:
а) схемой
A A A A
B B B B
C C C C
E E E E
б) с помощью матрицы (таблицы)
f1= 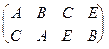 , f2=
, f2= 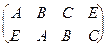
в) с помощью графа
В С С
А Е В А
f1 f2 Е
Теорема. Пусть Gx - множество всех преобразований множества Х¹Æ, тогда Gx относительно композиции преобразований образует группу.
Доказательство. Мы уже доказывали, что композиция преобразований ассоциативна. Проверим остальные аксиомы группы. Очевидно, что тождественное преобразование е множества X является единичным элементом множества Gx. Обратным элементом для преобразовании aÎGx является преобразование a-1ÎGx такое, что если a(x)=y, то a-1(y)=х, где x,yÎX. В самом деле,
(aa-1)(y)=a(a-1(y))=a(x)=y, то есть aa-1=e.
Аналогично доказывается, что a-1a=е. Итак, Gx относительно композиции преобразований является группой.
Преобразование a называют обратимым, если для него существует обратное преобразование a-1. Геометрические преобразования (биекции) являются обратимыми преобразованиями. Теория групп есть учение об обратимых преобразованиях. Заметим, что наглядно процедура получения обратного преобразования видна на примере подстановки, представленной в виде матрицы. Так, если
a= 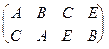 , то a-1=
, то a-1= 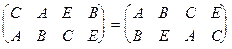 ,
,
то есть a-1 получается из a заменой строк.
Теперь мы переходим к центральному понятию параграфа - группе преобразований. Иногда некоторые подмножества группы gx сами являются группами относительно композиции преобразований. Такие подмножества называют группами преобразований.
Ясно, что сама Gх - группа преобразований.
Теорема. Для того, чтобы подмножество Gx’ÌGx было группой преобразований, достаточно, чтобы:
1) для любых a, bÎGx’, a·bÎGx’;
2) для всякого aÎGx’ и a-1ÎGx’ (доказать самостоятельно).
Поэтому группу преобразований множества X часто определяют как множество преобразований множества X, обладающее 1 и 2 свойствами.
Примеры группы преобразований. Множество всех перемещений плоскости, множество всех преобразований подобия являются группами преобразований плоскости.
Иногда свойства 1 и 2 называют свойствами замкнутости относительно композиции и перехода к обратному элементу. Не следует думать, что такое свойство замкнутости относительно композиции и перехода к обратному элементу присуще любому множеству преобразований. Например, множество осевых симметрий этим свойством не обладает: при композиции двух осевых симметрий получаются повороты или параллельные переносы, а не осевые симметрии. Заметим, что из условий 1 и 2 вытекает, что любая группа G преобразований содержит тождественное преобразование Е: она содержит хотя бы одно преобразование a, поэтому и a-1ÎG, тогда и преобразование a-1a=EÎG.
Важным примером группы преобразований является группа симметрий. Ее изучение - одна из главных задач этого параграфа.
Греческое слово “симметрия” в переводе на русский язык означает “соразмерность”. В древности симметричными называли фигуры, имеющие ось или центр симметрии. Многие архитектурные сооружения симметричны, вращающиеся части машин делают центрально-симметричными, причем ось вращения проходит через центр симметрии - это обстоятельство обеспечивает уравновешенность возникающих при вращении сил. Отличить симметричную фигуру от несимметричной легко, в этом нам помогает интуиция. Она подсказывает нам, что квадрат симметричнее ромба, а окружность симметричнее эллипса. Но одной интуиции бывает недостаточно, и важным инструментом при изучении свойств симметричных фигур являются так называемые группы симметрии. Введем общее понятие симметрии: назовем симметриями фигуры все ее перемещения, переводящие фигуру в себя. Например, ромб ABCD переходит в себя при осевых симметриях относительно прямых АС и BD. Поэтому он переходит в себя и при композиции этих симметрий то есть при центральной симметрии относительно точки О - точки пересечения диагоналей. Прямоугольник со сторонами разной длины имеет лишь четыре оси симметрии, а квадрат - восемь осей симметрии. Чем богаче множество симметрий фигуры, тем она симметричней. Что же такое группа симметрий геометрической фигуры?
Теорема. Пусть F - геометрическая фигура и GF - множество ее симмeтрий. Тогда относительно композиции преобразований GF образует группу.
Доказательство. Если f и g - элементы GF, то они переводят фигуру F в себя. Но тогда и преобразование fg переводит фигуру F в себя. Вместе с каждым преобразованием f множеству GF принадлежит и преобразование f-1, обратное f. Ведь если f отображает фигуру F на себя, то тем же свойством обладает и f-1 - при этом преобразовании все точки фигуры F возвращаются в исходное положение, то есть в точки той же фигуры. Итак, мы доказали, что множество GF симметрий фигуры вместе с любыми двумя преобразованиями f и g содержит и их композицию fg, а вместе с каждым преобразованием f - обратное ему преобразование f-1, то есть является группой преобразований.
В дальнейшем мы будем говорить не “множество симметрий фигуры F” а “группа симметрий фигуры F”, рассматривая множество симметрий фигуры относительно композиции преобразований. Итак, множество GF всех перемещений пространства (или плоскости), при которых данная фигура F отображается на себя с операцией композиции перемещений, образует группу симметрий фигуры F. Эта группа служит характеристикой cиммeтричности фигуры.
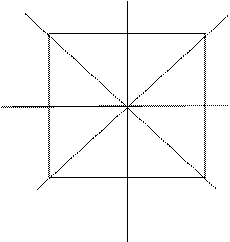
Группа симметрий окружности состоит из всех поворотов 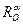 вокруг центра О окружности и всех осевых симметрий Sl c осями l, проходящими через точку О.
вокруг центра О окружности и всех осевых симметрий Sl c осями l, проходящими через точку О.
Квадрат имеет следующие виды симметрии:
а) тождественное перемещение е;
б) четыре осевые симметрии относительно средних линий и диагоналей квадрата;
 в) повороты
в) повороты 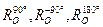 =ZO. Каждой из перечисленных симметрий квадрата ABCD соответствует подстановка на множестве его вершин:
=ZO. Каждой из перечисленных симметрий квадрата ABCD соответствует подстановка на множестве его вершин:
n m l
B A
o
k
c D
e= 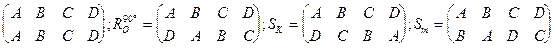 ;
;
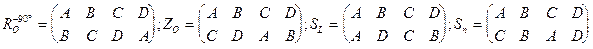 .
.
Для разностороннего треугольника группа симметрий состоит лишь из одного элемента - тождественного преобразования. У равнобедренного, но не равностороннего треугольника кроме тождественного преобразования в группу симметрий входит осевая симметрия относительно высоты, проведенной к основанию.




 B B
B B

 A C A C
A C A C
D
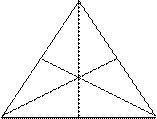
У равносторонних треугольников группа симметрий состоит из шести элементов: тождественное преобразование, три осевые симметрии относительно высот и два поворота 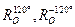 , где О - центр треугольника, то есть точка пересечения этих высот.
, где О - центр треугольника, то есть точка пересечения этих высот.
 B
B
O
A C
Докажем, что у равностороннего треугольника АВС нет иных симметрий, кроме описанных выше. Это следует из того, что при любой симметрии вершины треугольника переходят в вершины того же треугольника, а точки А, B, C можно переставлять друг с другом лишь шестью различными способами:
А®A A®B A®A A®C A®B A®C
B®B B®A B®C B®B B®C B®A
C®C C®C C®B C®A C®A C®B
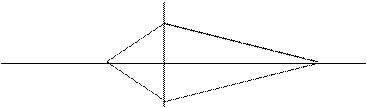
Рассмотрим группы симметрий для четырехугольников. Если в четырехугольнике нет сторон одинаковой длины, то, как и разносторонний треугольник, он имеет лишь одну симметрию - тождественное преобразование. Предположим, что у четырехугольника есть две смежные равные стороны, например АВ и AD.
 B
B
A C l
D
Тогда при симметрии относительно биссектрисы угла BAD точка А остается неподвижной, а точки В и D меняются местами. Поэтому, чтобы это преобразование было симметрией четырехугольника, точка O должна остаться неподвижной, то есть лежать на оси симметрии. В этом случае стороны CD и СВ равны.
Рассмотрим группу симметрий ромба. Множество симметрий ромба состоит из тождественного преобразования (е), вращения ромба вокруг центра на 180° (a), симметрий ромба относительно диагоналей (b и с).
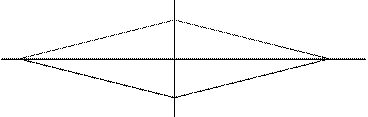 B
B
A C
D
Построим таблицу Кэли группы симметрий ромба, не являющегося квадратом. Она такова:
| e | a | b | c | |
| e | e | a | b | c |
| a | a | e | c | b |
| b | b | c | e | a |
| c | c | b | a | e |
Множество симметрий прямоугольника состоит из четырех перемещений: тождественного, центральной симметрии и двух осевых симметрий.
Упражнения
1. Доказать, что множество всех гомотетий с одним и тем же центром есть группа преобразований.
2. Будет ли множество параллельных переносов плоскости группой преобразований?
3. Пусть f,g - преобразования из группы преобразований GФ фигуры Ф. Доказать, что (fg)-1=g-1f-1. Верно ли это равенство в абстрактной группе G, то есть когда f,gÎG?
4. Найти композицию преобразований (fg)-1f.
5. Образует ли группу множество, состоящее из тождественного преобразования и осевой симметрии Sl?
Отметим, что множество различных групп преобразований бесконечно и каждая из них задает свою геометрию. Таким образом, существует бесконечно много разных геометрий. Например, если G - группа симметрий некоторой фигуры, то G есть группа преобразований этой фигуры, и поэтому она задает некоторую своеобразную “геометрию” этой фигуры. Такая групповая точка зрения на геометрические свойства фигур широко используется в физике атома и элементарных частиц. Мысль о том, что каждая группа преобразований определяет свою геометрию, была впервые высказана немецким математиком Клейном в лекции, которую он прочел в 1842 году при вступлении на должность профессора Эрлангентского университета. В этой лекции Клейн призвал переосмыслить все отдельные “геометрии” на основе групповой точки зрения. С тех пор эту точку зрения математики называют эрлангентской программой.
ПОДГРУППЫ
Определение. Пусть G - группа, НÌG, H называется подгруппой группы G, если выполняются два условия:
1. Для всяких а1, а2ÎН следует, что а1а2ÎН.
2. Для произвольного аÎН следует, что а-1ÎН.
Пример. Рассмотрим, является ли подгруппой группы Z относительно сложения множество H={x½x=3q, qÎZ}.
Проверим: по определению, 1) 3q1+3q2 = 3(q1+q2) = 3q Î H; 2) (3q)-1 = -3qÎH. Следовательно, Н - подгруппа группы Z по сложению.
Предложение. Пусть G - группа, Н - ее конечное подмножество и оно замкнуто относительно умножения, тогда Н - подгруппа группы G.
Доказательство. Докажем замкнутость Н относительно существования обратного элемента. Возьмем произвольный элемент аÎН. Если а=е, то а -1=е и а-1 ÎН. Пусть а¹е. Рассмотрим степени элемента а: a, a2, a3,..., am... - все эти элементы принадлежат Н (так как Н замкнуто относительно умножения по условию) Так как множество Н конечно, то все эти элементы различны быть не могут. Значит, существуют n,mÎÀ такие, что an=am. Пусть m>n ( в случае m<n доказательство проводится аналогично). Тогда m=n+kÞ an+k=an Þanak=aneÞ ak=eÞ aak-1=e.
Следовательно, ak-1 - обратный для а, то есть а-1=ak-1. Но aÎH, следовательно, ak-1 ÎH, то есть a-1ÎH. Таким образом, для произвольного aÎH получили a-1ÎH.
СВОЙСТВА ПОДГРУПП
1. Пересечение подгрупп группы G является подгруппой группы G. Пусть {Нj}jÎT - множество подгрупп группы G. Покажем, что их пересечение
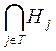 - тоже подгруппа.
- тоже подгруппа.
Доказательство
1. Покажем, что если два элемента принадлежат 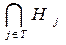 , то их произведение тоже принадлежит
, то их произведение тоже принадлежит 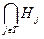 . Если x,yÎ
. Если x,yÎ 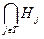 , то х, y принадлежат всем Hj, и, следовательно, xy принадлежит всем Нj, так как Нj - подгруппы, тогда xyÎ
, то х, y принадлежат всем Hj, и, следовательно, xy принадлежит всем Нj, так как Нj - подгруппы, тогда xyÎ 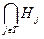 .
.
2. Покажите самостоятельно, что если xÎ 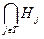 , то и x-1Î
, то и x-1Î 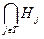 .
.
Упражнения
1. Определить, является ли группой каждое из следующих множеств, относительно указанных операций:
а) множество всех квадратных матриц второго порядка относительно умножения;
б) множество всех неособенных квадратных матриц второго порядка относительно умножения;
в) множество диагональных матриц второго порядка относительно умножения G= 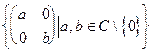 ;
;
г) множество всех матриц вида G= 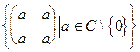 .
.
2. Какие из приведенных выше групп являются подгруппами друг друга?
3. Является ли подгруппой группы целых чисел относительно сложения множество Н следующего вида: H={x½x=5q, qÎZ}?
4. Доказать, что множествоJM всех биективных преобразований множества М есть группа относительно композиции преобразований.
5. Докажите утверждение: для того, чтобы непустое множество Н (НÌG) было подгруппой группы G, необходимо и достаточно, чтобы Н было группой относительно действия, введенного в G.
Одним из важнейших типов групп являются циклические группы. Определение. Пусть G - группа, МÌG. Подгруппой, порожденной множеством М, называется множество [М]= 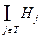 , МÌНj , где Нj - подгруппы группы G.
, МÌНj , где Нj - подгруппы группы G.
Другими словами, это пересечение всех подгрупп группы G, которые содержат М.
Пример. Пусть G - группа целых чисел по сложению. Найти подгруппу, порожденную множеством М={5,7}.
Решение. Так как 5 и 7 - взаимно просты, то существуют k1,k2ÎZ, такие, что 1=k1´5+k2´7. Заметим, что если какая-нибудь подгруппа Н группы G содержит числа 5 и 7, то она содержит и числа k1´5 и k2´7 (объясните). Следовательно, 1Î[{5,7}]. Возьмем произвольное tÎZ, тогда t=t´1Î[{5,7}]. Итак, мы получили, что [(5,7)]=Z.
Теорема. Пусть G - группа, МÌG. Тогда подгруппа, порожденная множеством М, состоит из тех и только тех x, которые представимы в виде [М]={xÎG½x=а1´ а2 ´...´an , где аiÎМ или аi-1Î М для всех i=l,...,n}.
Доказательство. Нужно показать равенство двух множеств. (Два множества равны тогда и только тогда, когда каждый элемент первого множества принадлежит второму, и наоборот.)
1. Пусть xÎT={xÎG½x=а1´ а2 ´...´an , где аiÎМ или аi-1Î М}. Покажем, что xÎ[М]. По определению, [М] - пересечение всех подгрупп, содержащих М. Пусть Н - произвольная подгруппа, содержащая М. Покажем, что xÎН (тогда получим, что х лежит в пересечении всех Н, содержащих М, а следовательно, хÎ[М]). Доказывать будем по индукции относительно числа множителей в выражении для х.
Пусть n=1. Тогда x=а1. По условию, а1Î М или 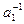 ÎМ. Если а1Î М , то
ÎМ. Если а1Î М , то
x= а1Î М ÌН, следовательно, xÎН. Если 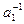 ÎМÌН, то, так как Н - подгруппа, (
ÎМÌН, то, так как Н - подгруппа, ( 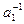 )-1ÎН, то есть a1ÎH и значит, xÎН.
)-1ÎН, то есть a1ÎH и значит, xÎН.
Предположим, что теорема верна для всех k<n, и докажем для k=n.
Пусть x=(а1а2 ...аn-1)an, где а1а2 ...аn-1ÎН по индуктивному предположению. По условию, anÎМÌН (тогда сразу получаем, что xÎН) или 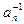 ÎМÌН. Так как Н - подгруппа ,то (
ÎМÌН. Так как Н - подгруппа ,то ( 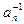 )-1=anÎН. Следовательно, получаем и в этом случае, что xÎН, поэтому xÎ[M]. То есть ТÌ[М].
)-1=anÎН. Следовательно, получаем и в этом случае, что xÎН, поэтому xÎ[M]. То есть ТÌ[М].
2) Нужно показать, что [М]ÌТ. Для этого сначала нужно проверить, будет ли множество Т подгруппой группы G (докажите это самостоятельно, пользуясь определением и свойствами групп). Из построения множества Т следует, что МÌТ. А так как [М] - пересечение всех подгрупп группы G, содержащих М, и Т - одна из таких подгрупп, значит, [М]ÌТ. Таким образом, равенство двух множеств доказано.
Определение. Пусть G - группа, aÎG, множество [а] называется циклической подгруппой группы G, порожденной элементом а.
Определение. Группа G называется циклической группой, если она совпадает c какой-нибудь своей циклической подгруппой, то есть, если существует аÎG такой, что G=[а].
Примечание. По определению [a]={...,a-3,а-2,а-1,а0 =е,а1,а2,а3,...}. Пусть xÎ[a], значит
x= а1а2 ...аn-1an=aa...aa-1...a-1=am, mÎZ.
Пример. Группа целых чисел относительно сложения является циклической, так как Z=[1].
[1] - это пересечение всевозможных подгрупп группы Z, которые содержат 1. Но если подгруппа содержит 1, то по определению подгруппы она содержит и обратный элемент (-1). Следовательно, (-1)Î[1]; 1+(-1)=0, то есть 0Î[1]; 1+1=2, то есть 2Î[1] и т.д. Аналогично с отрицательными числами. Итак, получили, что [1]=Z.
Теорема. Подгруппа циклической группы - циклическая.
Доказательство. Пусть G - циклическая группа, порожденная элементом a (G=[a]), H=[a], Н - подгруппа. Покажем, что Н - циклическая подгруппа. Для этого надо найти такой элемент bÎН, что Н=[b]. Так как НÌG, а G - циклическая группа, то Н состоит из целых степеней а. Если это только а0 (объясните, почему по крайней мере а0 должен принадлежать Н), то Н - циклическая подгруппа, порожденная элементом а0. Если в Н есть не только а0, то есть некоторая положительная степень элемента а (почему?). Рассмотрим akÎ H, k¹0. Если k>0, то это требуемое. Если k<0, тогда, так как Н - подгруппа, то (ak)-1=a-kÎ Н, -k>0. Следовательно, положительная степень элемента a в Н есть. Рассмотрим множество всех положительных показателей, с которыми а входит в Н. Это непустое множество. В нем, по аксиоме минимальности, существует наименьший элемент. Пусть это n0 ( 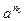 ÎН). Если 0<k<n0 , то akÏ Н. Положим b=
ÎН). Если 0<k<n0 , то akÏ Н. Положим b= 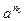 . Докажем, что H=[b] (надо доказать равенство двух множеств).
. Докажем, что H=[b] (надо доказать равенство двух множеств).
1. Покажем, что [b]ÌН. Пусть xÎ[b], следовательно, x=bt, где tÎZ. Но Н - подгруппа, bÎН, следовательно, x=btÎН. Мы взяли x из [b] и
получили, что xÎН.
2. Теперь покажем, что НÌ[b]. Пусть xÎН, следовательно, x=am. Разделим m на n0 с остатком: m=n0q+r, где 0£r<n0. Если r=0, то
am =( 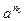 )q=bqÎ[b]. Допустим, что r¹0, следовательно, r>0. Равенство am =(
)q=bqÎ[b]. Допустим, что r¹0, следовательно, r>0. Равенство am =( 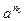 )q ar домножаем на (
)q ar домножаем на ( 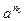 )-q слева, получим (
)-q слева, получим ( 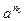 )-qam =ar, где amÎН,
)-qam =ar, где amÎН, 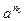 ÎН, значит (
ÎН, значит ( 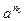 )-q ÎН. Получили, что arÎ Н. Но r<n0, а n0 - минимальная положительная степень элемента а, содержащаяся в Н. Следовательно, получено противоречие.
)-q ÎН. Получили, что arÎ Н. Но r<n0, а n0 - минимальная положительная степень элемента а, содержащаяся в Н. Следовательно, получено противоречие.
Таким образом, мы доказали, что m=n0q и x=am =bq Î[b].
Определение. Циклической группой k-го порядка называется группа, состоящая из k элементов.
Упражнения
1. Найти подгруппу группы G, порожденную множеством М={7,11}, где
а) G - группа целых чисел относительно сложения;
б) G - группа вещественных чисел (R\{0}) относительно умножения.
2. Показать, что циклическая подгруппа является абелевой группой, но исходная группа абелевой может не быть.
3. Докажите следующие утверждения:
1) пусть G=[a]. Если для всех m,nÎÀ из того, что m¹n следует, что am¹an, то G - бесконечная группа;
2) пусть G=[a]. Если существуют m,nÎZ такие, что m¹n, но am=an, то:
а) существует pÎÀ такое, что ap =е.
б) G = {е,а,a2 ,...,ak-1}, где k - наименьшее натуральное число такое, что ak=e.
в) элементы е,а,a2 ,...,ak-1 - различны.
4. Найти циклическую подгруппу группы комплексных чисел (C\{0}) по умножению, порожденную элементом i.
5. Пользуясь определением циклической группы k-го порядка и утверждением б) (см.упр.3), написать циклические группы 6-го и 8-го порядка. Выписать все подгруппы этих групп.
6. G - группа несобственных квадратных матриц второго порядка. Найти циклические подгруппы, порожденные матрицами:
а) 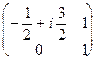 ; б)
; б) 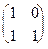 ; в)
; в) 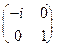 .
.
Дата добавления: 2020-10-25; просмотров: 674;