Синтаксическая мера информации
Рис. 1.1. Меры информации
Синтаксическая мера оперирует объемом данных и количеством информации Ia, выраженной через энтропию (понятие неопределенности состояния системы).
Семантическая мера оперирует количеством информации, выраженной через ее объем и степень содержательности.
Прагматическая мера определяется ее полезностью, выраженной через соответствующие экономические эффекты.
Синтаксическая мера информации
Эта мера количества информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту.
На сегодняшний день наиболее известны следующие способы количественного измерения информации: объемный, энтропийный, алгоритмический.
Объемный является самым простым и грубым способом измерения информации. Соответствующую количественную оценку информации естественно назвать объемом информации.
Объем информации – это количество символов в сообщении. Поскольку одно и то же число может быть записано многими разными способами, т. е. с использованием разных алфавитов, например двадцать один – 21– XXI– 11001, то этот способ чувствителен к форме представления (записи) сообщения. В вычислительной технике вся обрабатываемая и хранимая информация вне зависимости от ее природы (число, текст, отображение) представлена в двоичной форме (с использованием алфавита, состоящего всего из двух символов "0" и "1").
В двоичной системе счисления единица измерения – бит (bit – binary digit – двоичный разряд).
В теории информации бит – количество информации, необходимое для различения двух равновероятных сообщений; а в вычислительной технике битом называют наименьшую "порцию" памяти, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд. Это слишком мелкая единица измерения, на практике чаще применяется более крупная единица – байт, – равная 8 бит, необходимых для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256 = 28).
Широко используются также еще более крупные производные единицы информации:
1 килобайт (кбайт) = 1024 байт = 210 байт;
1 Мегабайт (Мбайт) = 1024 кбайт = 220 байт;
1 Гигабайт (Гбайт) = 1024 Мбайт = 230 байт.
В последнее время в связи с увеличением объемов обрабатываемой информации входят в употребление следующие производные единицы:
1 Терабайт (Тбайт) = 1024 Гбайт = 240 байт;
1 Петабайт (Пбайт) = 1024 Тбайт = 250 байт.
В десятичной системе счисления единица измерения – дит (десятичный разряд).
Пример.
Сообщение в двоичной системе в виде восьмиразрядного двоичного кода 1011 1011 имеет объем данных VД = 8 бит.
Сообщение в десятичной системе в виде шестиразрядного числа 275 903 имеет объем данных VД = 6 бит.
В теории информации и кодирования принят энтропийный подход к измерению информации. Получение информации о какой-либо системе всегда связано с изменением степени неосведомлен-ности получателя о состоянии этой системы. Этот способ измерения исходит из следующей модели.
Пусть до получения информации потребитель имеет некоторые предварительные (априорные) сведения о системе α. После получения сообщения b получатель приобрел некоторую дополнительную информацию I(b), уменьшившую его неосведомленность. Эта информация в общем случае недостоверна и выражается вероятностями, с которыми он ожидает то или иное событие. Общая мера неопределенности (энтропия) характеризуется некоторой математической зависимостью от совокупности этих вероятностей. Количество информации в сообщении определяется тем, насколько уменьшится эта мера после получения сообщения.
Так, американский инженер Р. Хартли (1928 г.) процесс получения информации рассматривает как выбор одного сообщения из конечного наперед заданного множества из N равновероятных сообщений, а количество информации i, содержащееся в выбранном сообщении, определяет как двоичный логарифм N (формула Хартли):
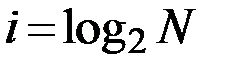 .
.
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: 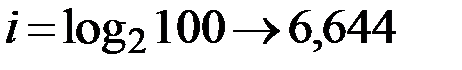 , т. е. сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицам информации.
, т. е. сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицам информации.
Другие примеры равновероятных сообщений:
1) при бросании монеты "выпала решка", "выпал орел";
2) на странице книги "количество букв четное", "количество букв нечетное".
Нельзя ответить однозначно на вопрос, являются ли равновероятными сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина". Все зависит от того, о каком именно здании идет речь. Если это, например, станция метро, то вероятность выйти из дверей первым одинакова для мужчины и женщины, а если это военная казарма, то для мужчины эта вероятность значительно выше, чем для женщины.
Для задач такого рода американский ученый Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе (формула Шеннона):
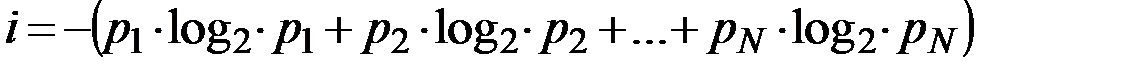 ,
,
где 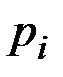 – вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
– вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
Легко заметить, что если вероятности 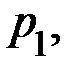 …
… 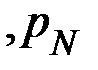 равны, то каждая из них равна
равны, то каждая из них равна 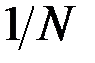 и формула Шеннона превращается в формулу Хартли.
и формула Шеннона превращается в формулу Хартли.
Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определенному кругу случаев, очерченному первоначальными допущениями.
В алгоритмической теории информации (раздел теории алгоритмов) предлагается алгоритмический метод оценки информации в сообщении. Любому сообщению можно приписать количественную характеристику, отражающую сложность (размер) программы, которая позволяет ее произвести.
Коэффициент (степень) информативности (лаконичности) сообщения определяется отношением количества информации к общему объему полученных данных:
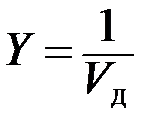 , причем 0 < Y < 1.
, причем 0 < Y < 1.
С увеличением Y уменьшаются объемы работ по преобразованию информации (данных) в системе. Поэтому необходимо стремиться к повышению информативности, для чего разрабатываются специальные методы оптимального кодирования информации.
1.4.2.2 Семантическая мера информации
Семантика – наука о смысле, содержании информации.
Для измерения смыслового содержания информации, т. е. ее количества на семантическом уровне, наибольшее признание получила тезаурусная мера, связывающая семантические свойства информации со способностью пользователя принимать поступившее сообщение. Одно и то же информационное сообщение (статья в газете, объявление, письмо, телеграмма, справка, рассказ, чертеж, радиопередача и т. п.) может содержать разное количество информации для разных людей в зависимости от их предшествующих знаний, уровня понимания этого сообщения и интереса к нему.
Для измерения количества семантической информации используется понятие "тезаурус пользователя", т. е. совокупность сведений, которыми располагает пользователь или система.
В зависимости от соотношений между смысловым содержанием информации S и тезаурусом пользователя Sp изменяется количество семантической информации Ic, воспринимаемой пользователем и включаемой им в дальнейшем в свой тезаурус. Характер такой зависимости показан на рисунке 1. 2.
Рис. 1. 2. Зависимость количества семантической информации, воспринимаемой потребителем, от его тезауруса IC = f(Sp)
Рассмотрим два предельных случая, когда количество семантической информации IC равно 0:
- при 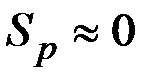 пользователь не воспринимает, не понимает поступающую информацию;
пользователь не воспринимает, не понимает поступающую информацию;
- при 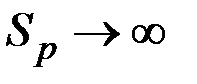 пользователь все знает и поступающая информация ему не нужна.
пользователь все знает и поступающая информация ему не нужна.
Максимальное количество семантической информации 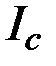 потребитель приобретает при согласовании ее смыслового содержания S со своим тезаурусом
потребитель приобретает при согласовании ее смыслового содержания S со своим тезаурусом 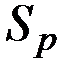 (
( 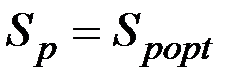 ), когда поступающая информация понятна пользователю и несет ему ранее неизвестные (отсутствующие в его тезаурусе) сведения.
), когда поступающая информация понятна пользователю и несет ему ранее неизвестные (отсутствующие в его тезаурусе) сведения.
Следовательно, количество семантической информации и новых знаний в сообщении, получаемое пользователем, является величиной относительной.
Относительной мерой количества семантической информации может служить коэффициент содержательности С, определяемый как отношение количества семантической информации к ее объему:
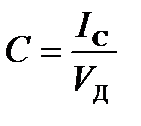 .
.
Дата добавления: 2016-05-31; просмотров: 8790;











