Практически все тепло идет на нагрев проводника
dQ = Gc 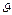 d
d  , (17.2)
, (17.2)
где G — масса проводника; c 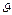 — удельная теплоемкость материала проводника при температуре
— удельная теплоемкость материала проводника при температуре  .
.
Известно, что G=glq, где g - плотность материала проводника, и С 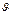 =С0(1+b
=С0(1+b  ), где С0 — теплоемкость проводника при
), где С0 — теплоемкость проводника при  =0°С; b — температурный коэффициент теплоемкости.
=0°С; b — температурный коэффициент теплоемкости.
Таким образом, процесс нагрева при КЗ определится уравнением
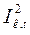 r
r 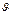 dt = Gc
dt = Gc 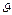 d
d  . (17.3)
. (17.3)
После подстановки в уравнение (17.3) развернутых значений r 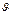 , G, c
, G, c 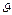 и перегруппировки членов получим:
и перегруппировки членов получим:
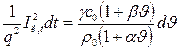 .
.
Проинтегрируем уравнение соответственно переменным: левую часть уравнения от 0 до tOTK (время отключения), а правую — от  н до
н до  к (начальное и конечное значения температур при КЗ):
к (начальное и конечное значения температур при КЗ):

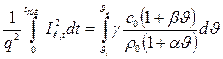 . (17.4)
. (17.4)
Рис. 17.1 Кривые определения температур нагрева проводников при КЗ
Таблица 17.1. Значение коэффициента k
| Проводник | Значение коэффициента k, мм4 ×°С/(А2×С)×10-2 |
| Алюминиевые шины, голые алюминиевые провода, кабели с алюминиевыми жилами и пластмассовой изоляцией, кабели с алюминиевыми сплошными жилами и бумажной пропитанной изоляцией То же с медными жилами Кабели с алюминиевыми многопроволочными жилами и бумажной пропитанной изоляцией То же с медными жилами | 1,054 0,4570 0,9350 0,4186 |
Обозначим Bk = 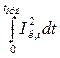 импульс квадратичного тока КЗ, пропорциональный количеству тепла, выделенного током КЗ в проводнике; по ГОСТ 26522 — 85
импульс квадратичного тока КЗ, пропорциональный количеству тепла, выделенного током КЗ в проводнике; по ГОСТ 26522 — 85
Вк — интеграл Джоуля. Метод вычисления Вк изложен ниже. Значение правой части (17.4) обозначим как fн/k при  н и fк/k при
н и fк/k при  К, где k — коэффициент, учитывающий удельное сопротивление и эффективную теплоемкость проводника (табл. 17.1).
К, где k — коэффициент, учитывающий удельное сопротивление и эффективную теплоемкость проводника (табл. 17.1).
Величина f является, как это видно из (17.4), сложной функцией температуры проводника, и если принять f независимой переменной, то можно записать  =j(f). Зависимость
=j(f). Зависимость  [°С]=j(f) приводится в справочной литературе и представлена, в частности, на рис. 17.1.С учетом принятых обозначений интегральное выражение (17.4) примет вид:
[°С]=j(f) приводится в справочной литературе и представлена, в частности, на рис. 17.1.С учетом принятых обозначений интегральное выражение (17.4) примет вид: 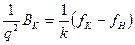 ,или
,или 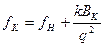 . (17.5)
. (17.5)
Уравнение (17.5) является исходным для определения температуры проводника  к к концу КЗ. Величину fн, характеризующую тепловое состояние проводника к моменту начала КЗ, можно определить по кривой рис. 17.1 по известной температуре проводника в предшествующем режиме работы
к к концу КЗ. Величину fн, характеризующую тепловое состояние проводника к моменту начала КЗ, можно определить по кривой рис. 17.1 по известной температуре проводника в предшествующем режиме работы  Н.
Н.
Определение  Нпроводят с использованием выражения
Нпроводят с использованием выражения 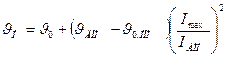
где  0 — температура окружающей среды;
0 — температура окружающей среды;  доп — длительно допустимая температура проводника;
доп — длительно допустимая температура проводника;  0,ном — поминальная температура окружающей среды (согласно ПУЭ
0,ном — поминальная температура окружающей среды (согласно ПУЭ  0,ном=25°С для воздуха, 15 °С — для земли и воды); Imах — максимальный ток нагрузки; Iдоп — длительно допустимый ток проводника.
0,ном=25°С для воздуха, 15 °С — для земли и воды); Imах — максимальный ток нагрузки; Iдоп — длительно допустимый ток проводника.
Если к fн прибавить величину kBК/q2, определяемую по известным значениям токов КЗ Iк, коэффициента k (табл. 17.1) и сечения q исследуемого проводника, то по (17.5) получим значение fK.
По кривым на рис. 17.1, используя fк, определяем конечное значение температуры проводника в режиме КЗ  к. Если
к. Если  к
к 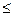
 К доп, то проводник термически стоек.
К доп, то проводник термически стоек.
Определение Вк для оценки термической стойкости производится приближенным способом из-за сложной зависимости тока КЗ от времени. При этом полный импульс квадратичного тока КЗ разбивается на две составляющие с учетом структуры полного тока КЗ по выражению: 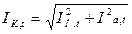 ;
;
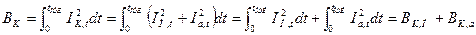 ; (17.6)
; (17.6)
здесь ВК,П , ВК,а — импульсы квадратичного тока КЗ соответственно от периодической и апериодической составляющих.
Импульс квадратичного тока КЗ определяется по-разному в зависимости от местонахождения точки КЗ. Можно выделить три характерных случая (по аналогии с расчетом тока КЗ): удаленное КЗ, КЗ вблизи генераторов или синхронных компенсаторов, КЗ вблизи группы мощных электродвигателей.
В первом случае периодическая составляющая тока КЗ является незатухающей во времени, т. е.
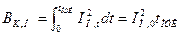 , (17.7)
, (17.7)
где IП,0 — начальное значение периодической составляющей тока КЗ, суммарное от всех источников.
Изменение апериодической составляющей тока КЗ описывается выражением 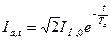 .
.
Импульс квадратичного тока КЗ от апериодической составляющей можно определить как
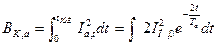 ,
,  а после преобразований
а после преобразований 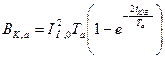 . (17.8)
. (17.8)
Если время tOTK равно или превышает Ta, что обычно имеет место, то можно принять 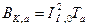 , (17.9)
, (17.9)
и полный импульс квадратичного тока КЗ определится из выражения 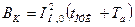 . (17.10)
. (17.10)
Данный способ рекомендуется при вычислении импульса квадратичного тока КЗ в цепях понизительных подстанций (исключение составляют КЗ на шинах 3-10 кВ подстанций, к которым подключены крупные электродвигатели или синхронные компенсаторы), в цепях высшего напряжения электростанций, в цепях генераторного напряжения электростанций, если место КЗ находится за реактором.
Наиболее сложным является случай определения импульса квадратичного тока при КЗ вблизи генераторов или синхронных компенсаторов, а также в цепях генераторного напряжения электростанций типа ТЭЦ. Решение производится различно в зависимости от мощности генераторов и их типа.
Для ориентировочных расчетов можно воспользоваться уравнением (17.10). При этом вычисленное значение импульса квадратичного тока КЗ будет несколько завышено, так как в действительности ток затухает. Но уточнять значение Вк, как правило, не требуется, поскольку проводники и аппараты, выбранные в мощных присоединениях (генератор, трансформатор связи и др.), по условиям длительного режима и электродинамической стойкости имеют значительные запасы по термической стойкости.
Известную трудность при расчетах Вк представляет собой определение значения постоянной Тa. При оценке Вк в случае КЗ на шинах электростанций по суммарному току КЗ приближенно можно считать Тa, равной:
Шины электростанции 6-10 кВ с генераторами 30-60 МВт .... 0,185с
Шины повышенного напряжения электростанции с трансформаторами:
32 МВ-А и выше ................... 0,115 с
100 МВ-А и выше .................. 0,14 с
При КЗ вблизи группы электродвигателей, например в системе собственных нужд ТЭС, необходимо учитывать их влияние на импульс квадратичного тока КЗ. Для определения суммарного импульса квадратичного тока КЗ с учетом электродвигателей рекомендуется пользоваться формулой
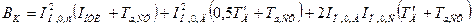 , (17.11)
, (17.11)
где
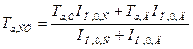 . (17.12)
. (17.12)
В этих выражениях IП,0,С , IП,0,Д , Tа,Д , Tа,с , TД¢ являются параметрами режима КЗ.
Для пользования формулами при нахождении Вк необходимо достаточно точно определять tOTK.
Согласно ПУЭ время отключения (время действия тока КЗ) tотк складывается из времени действия основной релейной защиты данной цепи tрз с учетом действия АПВ и полного времени отключения выключателя tотк,b:
tоTK = tр,з + tОТК,В (17.13)
Действующие нормативы рекомендуют для цепей генераторов 60 МВт и выше, учитывая их особую ответственность, принимать время tотк=4с, т.е. по времени резервной защиты.
Для упрощения анализа термической стойкости проводников часто используется понятие минимального сечения проводника qmin.
Минимальное сечение проводника, отвечающее требованию его термической стойкости при коротком замыкании, т. е. такое сечение, которое при заданном токе КЗ обусловливает нагрев проводника до кратковременно допустимой температуры, можно определить по формуле
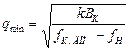 (17.14)
(17.14)
Значения fк,доп и fн следует определять по кривым рис. 17.1 для соответствующих температур  доп и
доп и  н.
н.
При приближенных расчетах минимальное сечение проводника, отвечающее требованию его термической стойкости при КЗ, можно определить по формуле
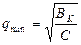 (17.15) где С — функция, значения которой приведены в табл. 17.2.
(17.15) где С — функция, значения которой приведены в табл. 17.2.
Очевидно, что проводник сечением q будет термически стойким, если выполняется условие q 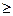 qmin.
qmin.
При выборе электрических аппаратов обычно не требуется определять температуру токоведущих частей, поскольку завод-изготовитель по данным специальных испытаний и расчетов гарантирует время и среднеквадратичный ток термической стойкости. Другими словами, в каталогах приводится значение гарантированного импульса среднеквадратичного тока КЗ, который выдерживается аппаратом без повреждений, препятствующих дальнейшей нормальной работе. Условие проверки термической стойкости в этом случае следующее:
Вк 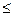 I2 тер tтер ,
I2 тер tтер ,
где Вк - расчетный импульс квадратичного тока КЗ, определяемый по изложенной выше методике; Iтер и tтер — соответственно среднеквадратичный ток термической стойкости и время его протекания (номинальные значения).
В ПУЭ и руководящих указаниях оговорен ряд случаев, когда допустимо не проверять проводники и аппараты на термическую стойкость при КЗ. Это касается проводов воздушных линий при отсутствии на них быстродействующего АПВ, аппаратов и проводников цепей, защищенных плавкими предохранителями, проводников цепей трансформаторов напряжения и некоторых других случаев.
Таблица 17.2. Значение функции С
| Проводник | Значение функции С А-с1/2/мм2 |
| Шины: алюминиевые медные Кабель: с алюминиевыми сплошными жилами и бумажной изоляцией с алюминиевыми многопроволочными жилами и бумажной изоляцией с медными сплошными жилами и бумажной изоляцией с медными многопроволочными жилами и бумажной изоляцией с алюминиевыми жилами и поливинилхлоридной изоляцией с медными жилами и поливинилхлоридной изоляцией с алюминиевыми жилами и полиэтиленовой изоляцией с медными жилами и полиэтиленовой изоляцией | при номинальном напряжении, кВ |
II. При КЗ за время dt в проводнике выделяется количество тепла
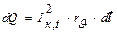
где Iк,t - действующее значение полного тока КЗ в момент t КЗ; rq - активное сопротивление проводника при данной его температуре q.
Обозначим 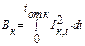 — импульс квадратичного тока КЗ, пропорциональный количеству тепла, выделенного током КЗ в проводнике.
— импульс квадратичного тока КЗ, пропорциональный количеству тепла, выделенного током КЗ в проводнике.
Определение Bк для оценки термической стойкости производится приближенным способом из-за сложной зависимости тока КЗ от времени. При этом полный импульс квадратичного тока КЗ разбивается на две составляющие с учетом структуры полного тока КЗ по выражению :
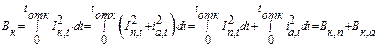
здесь Bк,п , Bк,а— импульсы квадратичного тока КЗ соответственно от периодической и апериодической составляющих.
Периодическая составляющая тока КЗ является незатухающей во времени, т. е.
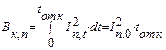
где Iп,0 -начальное значение периодической составляющей тока КЗ.
Изменение апериодической составляющей тока КЗ описывается выражением
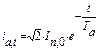
Импульс квадратичного тока КЗ от апериодической составляющей можно определить как
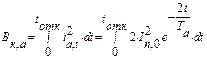
а после преобразований
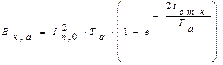
Если время tотк равно или превышает Ta, что обычно имеет место, то можно принять
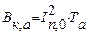 ,
,
и полный импульс квадратичного тока КЗ определится из выражения
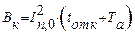 .
.
Согласно ПУЭ время отключения (время действия тока КЗ) tотк скла-дывается из времени действия основной релейной защиты данной цепи tрз с учетом действия АПВ и полного времени отключения выключателя tотк,В:
tотк = tp,з + t отк,В
Для упрощения анализа термической стойкости проводников часто используется понятие минимального сечения проводника qmin.
Минимальное сечение проводника, отвечающее требованию его термической стойкости при коротком замыкании, т. е. такое сечение, которое при заданном токе КЗ обуславливает нагрев проводника до кратковременно допустимой температуры, можно определить по формуле
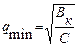 ,
,
где С - функция, значения которой принимаются по таблицам.
Очевидно, что проводник сечением q будет термически стойким, если выполняется условие q ³qmin.
При выборе электрических аппаратов обычно не требуется определять температуру токоведущих частей, поскольку завод-изготовитель гарантирует время и среднеквадратичный ток термической стойкости. Другими словами, в каталогах приводится значение гарантированного импульса среднеквадратичного тока КЗ, который выдерживается аппаратом без повреждений, препятствующих дальнейшей нормальной работе. Условие проверки термической стойкости в этом случае следующее:
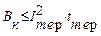 ,
,
где Bк — расчетный импульс квадратичного тока КЗ, определяемый по изложенной выше методике; Iтер и tтер - соответственно среднеквадратичный ток термической стойкости и время его протекания (номинальные значения).
В ПУЭ и руководящих указаниях оговорен ряд случаев, когда допустимо не проверять проводники и аппараты на термическую стойкость при КЗ. Это касается проводов воздушных линий при отсутствии на них быстродействующего АПВ, аппаратов и проводников цепей, защищенных плавкими предохранителями, проводников цепей трансформатора напряжения и некоторых других случаев.
Дата добавления: 2016-07-22; просмотров: 2916;











