МОЩНОСТЬ ТРЕХФАЗНОЙ СИСТЕМЫ И ЕЕ ИЗМЕРЕНИЕ

Активная мощность трехфазной системы Р является суммой фазных активных мощностей, а для каждой из них справедливо основное выражение активной мощности цепей переменного тока. Следовательно, фазная активная мощность Р_ф = ЗU_фI_фсоs j и при симметричной нагрузке активная мощность трехфазного устройства

P = 3 P_Ф = 3 U_Ф I_Ф cos j (3.7)

Но в трехфазных установках в большинстве случаев приходится выражать активную мощность устройства не через фазные, а через линейные величины. Это легко сделать на основании соотношений фазных и линейных величин, заменив в выражении активной мощности фазные величины линейными. При соединении звездой U_Ф = U_Л/Ö3 ; I_Ф = I_Л, а при соединении треугольником U_Ф = U_Л; I_Ф = I_Л/ÖЗ .После подстановки этих выражений в формулу (3.7) получим одно и то же выражение для активной мощности трехфазной симметричной установки:

P = 3U_Ф I_Ф cos j = Ö3 U_Л I_Л cos j

Хотя это выражение относится только к активной мощности симметричной системы, тем не менее им можно руководствоваться в большинстве случаев, так как в промышленных устройствах основная нагрузка редко бывает несимметричной.

Реактивная мощность в симметричной системе, так же как и полная мощность, выражается через линейные величины подобно активной мощности:

Q = 3Q_Ф = 3U_Ф I_Ф sin j = Ö3 U_Л I_Л sin j

и

S = 3 U_Ф I_Ф = Ö3 U_Л I_Л

Простейшие условия измерения активной мощности трехфазной системы имеются в том случае, если фазы приемников соединены звездой с доступной нейтральной точкой. В этом случае для измерения мощности одной фазы цепь тока ваттметра соединяют последовательно с одной из фаз приемника (рис. 3.12а), а цепь напряжения включают под напряжение той фазы приемника, в которую включена цепь тока ваттметра, т. е. зажимы цепи напряжения ваттметра присоединяются один к линейному проводу, а второй—к нейтральной точке приемника. В подобных условиях измеренная мощность

P_ИЗ = P_Ф = U_Ф I_Ф cos j

а мощность симметричного приемника

P =3 P_ИЗ =3 U_Ф I_Ф cos j

Часто нейтральная точка недоступна или фазы приемника соединены треугольником. Тогда применяется измерение с помощью искусственной нейтральной точки (рис. 12 б).

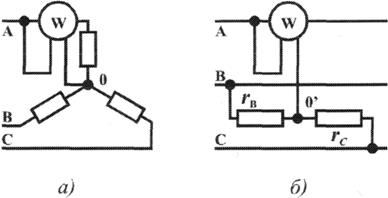
Рис. 3.12 Схема измерения активной мощности в симметричной трехфазной системе:

а — при доступной нейтральной точке,

б — с искусственной нейтральной точкой

Такая точка (точнее узел) составляется из цепи напряжения ваттметра с сопротивлением r_вт._н и двух добавочных резисторов С такими же сопротивлениями. При таком соединении цепь напряжения ваттметра находится под фазным напряжением, а через цепь тока прибора проходит фазный ток. Следовательно, и при таком измерении

P = 3 P_ИЗ

Для измерения активной мощности в четырехпроводной установке (т. е. установке с нейтральным проводом) при несимметричной нагрузке применяют способ трех ваттметров (рис. 3.13). В такой установке каждый из ваттметров измеряет активную мощность одной фазы, а активная мощность установки определяется как сумма мощностей, измеренных тремя ваттметрами:

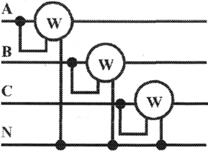
Рис. 3.13 Схема измерения активной мощности в трехфазной четырехпроводной системе (способ трех ваттметров)

В трехпроводных сетях при несимметричной нагрузке мощность измеряют способом двух ваттметров.

Если включить два ваттметра в трехпроводную систему постоянного тока (рис. 3.14), то они будут измерять мощность всей установки. При этом не имеет значения, каковы напряжения отдельных цепей, объединенных в трехпроводную систем. Если вместо постоянных тока и напряжения рассматривать мгновенные значения напряжений и токов трехфазной системы, то в таких условиях ваттметры будут показывать средние значения мгновенных мощностей, т. е. активные мощности. Но следует иметь в виду, что хотя Р = P₁ + Р₂, мощность системы равна сумме показаний двух ваттметров, но эта сумма алгебраическая, т. е. показание одного из ваттметров может быть отрицательным — стрелка одного из ваттметров может отклоняться в обратную сторону, за нуль шкалы. Чтобы отсчитать в таких условиях показание ваттметра нужно переключить зажимы цепи напряжения. Показания прибора после такого переключения следует считать отрицательными.

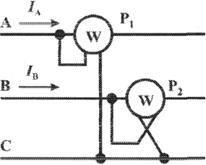
Рис. 3.14 Схема измерения активной мощности в трехфазной трехпроводной системе (способ двух ваттметров)

Пример. Трехфазный симметричный потребитель электроэнергии с сопротивлением фаз Zа = Zь = Zc = Zф = R = 10 Ом соединен «звездой» и включен в трехфазную сеть с симметричным линейным напряжением Uл = 220 В (рис.3.15). Определить токи в фазных и линейных проводах, а также потребляемую активную мощность в режимах:

а) при симметричной нагрузке;

б) при отключении линейного провода;

в) при коротком замыкании той же фазы нагрузки.

Построить для всех трех режимов топографические диаграммы напряжений и показать на них вектора токов.

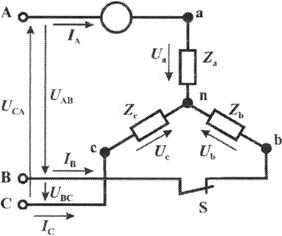
Рис. 3.15.

а) Решение. Фазные напряжения при симметричной нагрузке: Ua = Ub = Uc = Uф = Uл/Ö3 = 220Ö3 = 127 В. Фазные токи при этой нагрузке: I_Ф = Uф/Rф = 127/10 = 12,7 А. Линейные токи при симметричной нагрузке: I_А = I_C = I_Л = I_ф = 12,7 А, так как симметричный трехфазный потребитель электроэнергии соединен «звездой».

Активная мощность трехфазного симметричного потребителя:
Р = 3Рф = 3Uф × Iф cos j = 3 × 127 × 12,7 ×1 = 4850 Вт = 4,85 кВт или Р = Ö3 Uл Iл cos j_ф= Ö3 × 220 × 12,7 × 1 = 4850 Вт= 4,85 кВт, где
cos j_ф = 1 при Z_Ф = R_Ф.

Векторная диаграмма напряжений и токов приведена на рис.3.16.

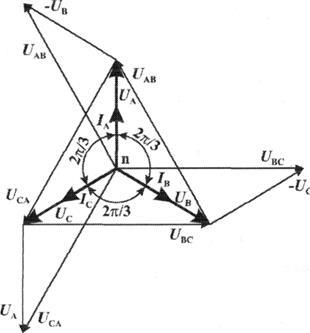
Рис. 3.16.

б)Решение Ток в линейных проводах аА и сС при обрыве линейного провода ЬВ (выключатель S разомкнут); так как сопротивление фазы Zb = ¥ (I_В = 0), а Za = R и Zc = R включены последовательно на линейное напряжение U_CA = U_Л = 220 B; I_A = I_C = I = U_CA/(R + R) = 220/(10 + 10) = 11 А.

Напряжение на фазах потребителя при обрыве линейного провода ЬВ (нейтральная точка п в этом случае соответствует середине вектора линейного напряжения U_CA): Ua = Uc = U_CA/2 = 220/2 = 110 B.

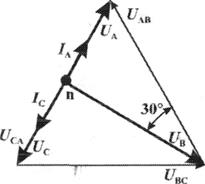
Рис. 3.17.

Напряжение между проводом фазы В и нейтральной точкой п определяют из векторной диаграммы (рис. 3.17): Uc = Uл cos p/6 = 220 × 0.866 = 190,5 B.

Активная мощность потребителя при обрыве линейного провода ЬВ: Р = Р_А + Р_С = 2 I² R_Ф = 2 × 11² × 10 = 2420 Вт = 2,42 кВт.

в) Для условия задачи определить фазные напряжения U_Ф и токи I_Ф, активную мощность Рк потребителя при коротком замыкании фазы Zb, построить векторную диаграмму для этого случая рис. 3.18.

Рис. 3.18

Решение. В данном случае Zb = 0 и Ub = 0, нейтральная точка п переместится в точку В, при этом фазные напряжения Uc = U_BC, Uа = U_АВ, т.е. фазные напряжения равны линейным напряжениям (Uф = U_Л). При этом фазные токи: I_A = I_C = Uл/R = 220/10 = 22 А. Ток I_В при коротком замыкании в соответствии с первым законом Кирхгофа для нейтральной точки п: I_A + I_B + I_C = 0 или -I_B = I_A + I_C.

Из прямоугольного треугольника на векторной диаграмме рис. 3.19 имеем: (-I_B/2)² + (I_A/2)² = I² _А, откуда I_B = Ö3 I_A = Ö3 × 22 ≅ 38 А. При этом I_А = U_Л/Za = Iс = U_Л/Zc = Uл/R = 220/10 = 22 А.

Активная мощность цепи при коротком замыкании: Рк = Р_А + P_C = 2 × I²ф R = 2 × 222 × 10 = 9680 Вт = 9,68 кВт. Векторная диаграмма напряжений и токов приведена на рис. 3.19

Рис. 3.19