Погрешности измерений и их оценки
Известно, что причиной появления погрешностей является несовершенство используемых СИ и неточность передачи рабочим СИ размеров единиц соответствующих ФВ. Несовершенство СИ является причиной возникновения погрешностей результата измерений при неизменных внешних условиях, а также вследствии различных условий проведения эксперимента (изменение температуры, влажности, давление и т. п.).
Кроме того, погрешность может быть обусловлена методом измерения. Так, например, при исследовании физических полей (температурных, магнитных и др.) сам датчик искажает топографию поля, т. к. обладает собственным полем и, следовательно, интересующая нас величина данным методом принципиально не может быть измерена абсолютно точно.
В процессе измерения в большинстве случаев участвует человек (субъект), который, в силу своих ограниченных физиологических возможностей, также может являться причиной возникновения погрешности.
Таким образом, погрешность измерения Δ в общем случае можно представить в виде следующих составляющих:
· инструментальной погрешности 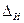 ;
;
· методической погрешности 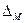 ;
;
· погрешности отсчета 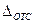 .
.
Рассмотрим каждую из этих составляющих более подробно.
Инструментальная погрешность ( 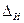 ) – погрешность от несовершенства СИ. Эту погрешность, согласно ГОСТ 8.009–84, подразделяют на основную
) – погрешность от несовершенства СИ. Эту погрешность, согласно ГОСТ 8.009–84, подразделяют на основную 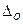 , дополнительную
, дополнительную 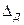 , динамическую
, динамическую 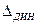 и погрешность, обусловленную взаимодействием СИ и объекта
и погрешность, обусловленную взаимодействием СИ и объекта 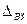 .
.
· 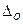 –это погрешность при условиях принятых за нормальные, т. е. при фиксированных значениях неинформативных ФВ (температуре, давление, напряжении питания и т. п.); влияющих на результат;
–это погрешность при условиях принятых за нормальные, т. е. при фиксированных значениях неинформативных ФВ (температуре, давление, напряжении питания и т. п.); влияющих на результат;
· 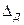 возникает при отклонении влияющих величин от значений, принятых за нормальные. Например, дополнительная погрешность от температуры;
возникает при отклонении влияющих величин от значений, принятых за нормальные. Например, дополнительная погрешность от температуры;
· 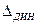 обусловлена инерционными свойствами СИ. Если СИ безинерционное, то
обусловлена инерционными свойствами СИ. Если СИ безинерционное, то 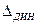 =0.
=0.
При использовании СИ на практике должны быть известны его метрологические характеристики, т. е. характеристики оказывающие влияние на результат. Основные характеристики (класс точности, предел измерения, параметры номинальной функции преобразования, цена деления и т.п.) указываются в технической документации на СИ, а наиболее важные из них наносятся наносятся непосредственно на СИ. При этом отклонение метрологических характеристик от номинальных значений, которые вызывают погрешности, носят вероятностный характер поэтому для них должны быть установлены предельные допустимые значения. Для этого осуществляют нормирование метрологических характеристик СИ, которое заключается в установлении границ для отклонений реальных значений параметров СИ от их номинальных значений.
К числу важнейших метрологических характеристик СИ относится погрешность. Нормирование погрешностей СИ необходимо для оценивания погрешности измерения и состоит в установлении предела допускаемой погрешности, под которым понимается наибольшая по модулю погрешность СИ, при которой оно может быть признано годным и допущено к применению.
При нормировании погрешностей СИ определяют пределы допускаемых основной и всех дополнительных погрешностей, а также нормальные условия и допускаемые отклонения от нормальных значений всех влияющих величин. С целью ограничения номенклатуры выпускаемых СИ и упорядочения требований к ним ГОСТ устанавливает классы точности. Класс точности – это обобщенная характеристика СИ, определяемая пределами основной и дополнительной погрешностей. Способы нормирования метрологических характеристик, общие для всех видов средств измерения электрических величин, содержатся в ГОСТ 8.401–80.
Для получения максимально точного результата важно правильно выбрать СИ, так как в противном случае может возникнуть погрешность от взаимодействия СИ и объекта измерений 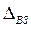 , которая является следствием несогласования в входного импеданса СИ и выходного импеданса объекта измерения.
, которая является следствием несогласования в входного импеданса СИ и выходного импеданса объекта измерения.
Например, при измерении вольтметром V с входным сопротивлением RVнапряжения на зажимах активного двухполюстника с выходным сопротивлением Rвых (рис.2.2) при выполнении условия Rвых< RV , возникает относительная погрешность [2.6]
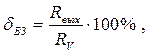 (2.1)
(2.1)
которая обусловлена уменьшением напряжения на зажимах двухполюстника за счет величины сопротивления вольтметра (при RV → ∞, 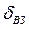 = 0).
= 0).
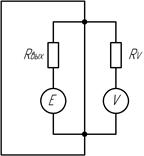
Рис. 2.2. Схема измерения напряжения вольтметром с конечным
внутренним сопротивлением
При измерении тока в замкнутой цепи с помощью амперметра А (рис.2.3) с внутренним сопротивлением  возникает погрешность
возникает погрешность
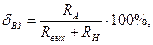 (2.2)
(2.2)
которая возникает из-за увеличения суммарного сопротивления (при 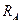 =0,
=0, 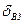 =0). В общем случае подключение реального СИ может существенно измерить режим работы исследуемой схемы, что особенно важно при измерении в целях переменного тока и напряжения. В этом случае необходимо учитывать реактивную (индуктивную, емкостную) составляющую импедансе.
=0). В общем случае подключение реального СИ может существенно измерить режим работы исследуемой схемы, что особенно важно при измерении в целях переменного тока и напряжения. В этом случае необходимо учитывать реактивную (индуктивную, емкостную) составляющую импедансе.

Рис. 2.3. Схема измерения тока амперметром с конечным
внутренним сопротивлением
Методическая погрешность 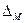 возникает от несовершенства применяемого метода измерения. Эта погрешность может возникать также из-за недостатка знаний о происходящих при измерении процессах, из-за неточности расчетных формул, в результате линеаризации функций преобразования. Выявление источников
возникает от несовершенства применяемого метода измерения. Эта погрешность может возникать также из-за недостатка знаний о происходящих при измерении процессах, из-за неточности расчетных формул, в результате линеаризации функций преобразования. Выявление источников 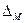 выполняют путем тщательного анализа всех причин возникновения.
выполняют путем тщательного анализа всех причин возникновения.
Погрешность отсчета 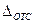 для аналоговых СИ определяется по формуле
для аналоговых СИ определяется по формуле
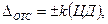 (2.2)
(2.2)
где k–коэффициент, зависящий от того, до каких долей деления шкалы СИ производится округление при отсчете (если до половины деления, то k=0,5 , если до десятой доли, то k=0,1); ЦД - центр деления СИ.
В общем случае, все вышеуказанные составляющие погрешности содержат систематическую и случайную части. Источниками систематической погрешности могут быть все элементы процесса измерения: метод, СИ и субъект (экспериментатор).
Методическая систематическая составляющая может быть исключена в каждом конкретном случае индивидуально, на основе анализа применяемого метода, результаты которого существенно зависят от квалификации экспериментатора.
Инструментальные систематические погрешности выявляется поверкой СИ. Поверку осуществляют сравнением показаний рабочего (поверяемого) с показаниями образцового прибора. В результате этой процедуры определяют поправку, с помощью которой можно корректировать показания рабочего СИ.
Субъективные систематические погрешности связаны с индивидуальными качествами экспериментатора. Для их уменьшения необходимо точно соблюдать правила эксплуатации СИ, а экспериментатор иметь соответствующие навыки. Существует ряд методов, позволяющих получить исправленный результат измерений, т. е. свободный от систематических погрешностей. Это метод замещения, метод противопоставления, метод компенсации по знаку и др.
Метод замещения осуществляется путем замены измеряемой величины известной величиной так, чтобы воздействием известной величины привести СИ в то состояние, которое оно имело при воздействии измеряемой величины.
Пример. Измерив напряжение на зажимах источника напряжения рабочим СИ (вольтметром) получили результат 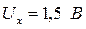 . Далее, подав на вольтметр напряжение от регулируемого образцового источника, добиваемая показаний вольтметра 1,5 В. При этом напряжение на зажимах образцового источника оказывается равным 1,65 В. Следовательно, для исправления результата измерении необходимо внести поправку
. Далее, подав на вольтметр напряжение от регулируемого образцового источника, добиваемая показаний вольтметра 1,5 В. При этом напряжение на зажимах образцового источника оказывается равным 1,65 В. Следовательно, для исправления результата измерении необходимо внести поправку 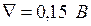 .
.
Метод противопоставления удобнее рассмотреть на конкретном примере. Пусть необходимо взвесить массу 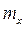 на рычажных весах (рис.2.4). Условие равновесия весов
на рычажных весах (рис.2.4). Условие равновесия весов 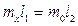 , тогда
, тогда 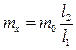 . Если
. Если  , то
, то 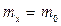 . В случае если в силу технологического разброса
. В случае если в силу технологического разброса 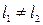 , то возникает систематическая погрешность. Для исключения ее взвешивание осуществляют в два этапа. Сначала взвешивают груз
, то возникает систематическая погрешность. Для исключения ее взвешивание осуществляют в два этапа. Сначала взвешивают груз 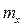 – уравновешивающая масса
– уравновешивающая масса  . Затем
. Затем 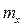 перемещают на другую чашу весов и вновь уравновешивают, но другой массой
перемещают на другую чашу весов и вновь уравновешивают, но другой массой  .
.
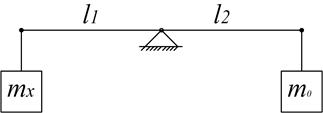
Рис. 2.4. Измерение массы методом противопоставления
Получаем систему уравнений
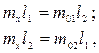
решая ее относительно 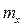 , получим
, получим

Видно, что длины плеч не входят в результат измерения, т.е. систематическая погрешность отсутствует.
Метод компенсации погрешности по знаку. Этот метод предполагает два этапа измерения, выполняемых так, чтобы систематическая погрешность входила в показания СИ не каждом этапом с разными знаками. За результат применяют полусумму показаний.
Пример. Измерить ЭДС потенциометром постоянного тока, имеющим паразитную термоЭДС. При выполнении одного измерения получаем результат Е1. Затем меняем полярность измеряемой ЭДС (направление тока в потенциометре). Вновь делаем его уравновешивание – получаем ЭДС Е2. Пусть термоЭДС вносит в результат измерения погрешность 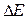 , тогда
, тогда 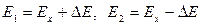 . Отсюда
. Отсюда 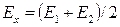 и в это выражение термоЭДС не входит.
и в это выражение термоЭДС не входит.
Метод рандомизации предполагает измерение одной и той же величины различными методами. Систематические погрешности каждого из них для всей совокупности является случайными величинами. При увеличении числа используемых систематические погрешности взаимно компенсируются.
Все сказанное относится к постоянным систематическим погрешностям, которые могут быть скомпенсированы введением соответствующих поправок. Сложнее обстоит дело, если систематические погрешности - переменные. В этом случае также разработаны различные методы и приемы.
Графический метод является наиболее простым способом обнаружения переменной систематической погрешности. В этом случае строится график последовательности неисправленных значений результатов наблюдений, на котором строят плавную огибающую, она и отражает характер изменения результата измерения. Если прослеживается некоторая тенденция, то можно говорить о наличии систематической погрешности.
Метод симметричных наблюдений. Пусть имеем измерительный преобразователь с функцией преобразования  , где
, где 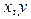 –входная и выходная величины;
–входная и выходная величины;  –коэффициент преобразования, погрешность которого изменяется во времени по линейному закону
–коэффициент преобразования, погрешность которого изменяется во времени по линейному закону 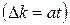 т. е.
т. е. 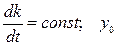 - постоянная.
- постоянная.
Алгоритм измерения осуществляется по следующему закону. Выходная величина 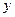 трижды измеряется через равные промежутки времени
трижды измеряется через равные промежутки времени 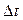 , при этом на вход преобразователя при первом и третьем измерении подается образцовый измерительный сигнал
, при этом на вход преобразователя при первом и третьем измерении подается образцовый измерительный сигнал 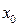 . В этом случае имеем систему уравнений
. В этом случае имеем систему уравнений
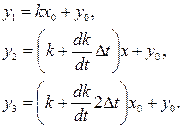
Решая ее относительно измеряемой величины х, получаем
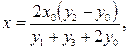
т.е. результат измерения не зависит от вариаций коэффициента 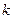 . Кроме рассмотренных выше существует ряд статистических методов обнаружения систематических погрешностей (метод Аббе, Фишера и др.), которые основаны на анализе выборочных значений
. Кроме рассмотренных выше существует ряд статистических методов обнаружения систематических погрешностей (метод Аббе, Фишера и др.), которые основаны на анализе выборочных значений 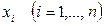 и будут рассмотрены в дальнейшем.
и будут рассмотрены в дальнейшем.
При проведении измерений, в силу множества независимых друг от друга причин, возникает случайная составляющая погрешности. Очевидно, что предсказать результат отдельного наблюдения и исправить его введением соответствующей поправки невозможно, можно лишь с определенной вероятностью утверждать, что истинное значение измеряемой величины находится в пределах некоторого интервала. Поскольку поведение этих погрешностей носит случайный характер, то их описание должно основываться на вероятностно-статическом математическом аппарате.
Известно, что наиболее универсальным способом описания случайных величин являются интегральные и дифференциальные функции распределения, которые характеризуются своими числовыми характеристиками. Однако, эти характеристики могут быть определены только на большом объеме статистического материала. На практике все результаты измерения и их погрешности являются величинами дискретными, т. е. принимают некоторое значение 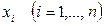 , а количество этих значений n конечно и счетно.
, а количество этих значений n конечно и счетно.
В этом случае возникает задача оценки случайных величин (погрешностей) на основе выборок конечного объема т. е. ряда значений 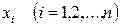 , принимаемых случайной величиной х в n независимых опытах (измерениях). Выборка должна быть репрезентативной (представительной), т.е. хорошо отражать свойства генеральной совокупности, а оценки, получаемые по статическому материалу – обладать свойствами состоятельности, несмещенности и эффективности.
, принимаемых случайной величиной х в n независимых опытах (измерениях). Выборка должна быть репрезентативной (представительной), т.е. хорошо отражать свойства генеральной совокупности, а оценки, получаемые по статическому материалу – обладать свойствами состоятельности, несмещенности и эффективности.
Состоятельность оценки означает, что при увеличении числа наблюдений она стремится к истинному значению оцениваемой величины.
Оценка называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемой величины. Если таких оценок несколько, лучшей будет та, которая имеет меньшую дисперсию. Чем меньше дисперсия оценки, тем более эффективной считают эту оценку.
Выбор соответствующей оценки зависит от вида функции распределения и от имеющихся соглашений по этому вопросу, регламентируемых в рамках законодательной метрологии. В практике измерений, чаще всего, имеют место нормальная и равномерная плотности распределения вероятностей. Так, в ГОСТ 8.207-76 «ГСИ. Прямые измерения с многократными наблюдениями» указывается, что приведенные в нем методы установлены для результатов наблюдений, принадлежащих нормальному закону распределения. Нормальное распределение имеет огромное значение для теории обработки результатов измерений. Согласно центральной предельной теореме теории вероятности закон распределения суммарной погрешности измерений близок к нормальному всякий раз, когда результаты наблюдений формируются под влиянием большого числа независимо действующих случайных составляющих, каждая из которых оказывает незначительное влияние по сравнению с суммарной погрешностью. Помимо этого, нормальный закон позволяет вести расчеты даже тогда, когда действующий закон неизвестен, так как нормальный закон дает чаще увеличенный, чем уменьшенный доверительный интервал [2.3].
Практически, суммарное воздействие даже сравнительно небольшого числа независимых случайных составляющих (n>4) приводит к закону распределения погрешностей измерения близкого к нормальному.
В аналитической форме нормальный закон распределения случайной величины х имеет вид
 (2.4)
(2.4)
где 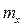 –математическое ожидание;
–математическое ожидание; 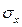 –среднеквадратическое отклонение.
–среднеквадратическое отклонение.
График нормального распределения представлен на рис.2.5.
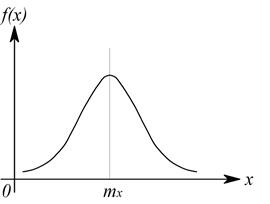
Рис.2.5. Нормальный закон распределения
Если переместить начало координат в центр распределения  , а по оси абсцисс откладывать погрешность
, а по оси абсцисс откладывать погрешность  , то получим кривую нормального распределения случайной погрешности (рис.2.6).
, то получим кривую нормального распределения случайной погрешности (рис.2.6).
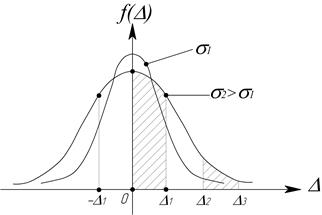
Рис.2.6. Нормальный закон распределения для различных s
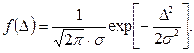 (2.5)
(2.5)
Рассмотрим наиболее важные свойства нормального распределения.
· Погрешности, одинаковые по величине, но противоположные по знаку, имеют одинаковую плотность вероятности (рис.2.6). Это означает, что при достаточно большом числе наблюдений такие погрешности встречаются одинаково часто (с одинаковой вероятностью). Отсюда следует что при нормальном распределении математическое ожидание случайной погрешности равно нулю.
· При нормальном законе распределения малые погрешности встречаются чаще, чем большие. Как следует из рис.2.6, вероятность проявления погрешности в интервале от 0 до 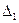 будет больше, чем в интервале от
будет больше, чем в интервале от 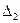 до
до 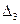 .
.
· Чем меньше СКО, тем меньше рассеивание результатов наблюдений и тем больше вероятность того, что большинство случайных погрешностей в этих наблюдений будет мало, т. е. качество измерений тем выше, чем меньше СКО случайных погрешностей.
Количественная оценка случайных погрешностей и установление границ погрешности результата измерения осуществляется в соответствии со стандартами и может быть представлена в виде:
· предельной погрешности,
· интервальной оценки;
· числовых характеристик закона распределения.
Если есть ряд наблюдений 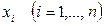 , полученных в результате измерительного эксперимента, то можно вычислить оценки математического ожидания (МО) и среднеквадратического отклонения (СКО)
, полученных в результате измерительного эксперимента, то можно вычислить оценки математического ожидания (МО) и среднеквадратического отклонения (СКО)
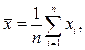 (2.6)
(2.6)
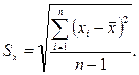 (2.7)
(2.7)
Это точечные оценки числовых характеристик функции распределения случайной величины. Выражение (2.6) представляет собой оценку МО результата измерения и может стать оценкой истинного значения измеряемой величины только после исключения систематической составляющей. Значение 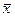 и
и 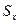 не полностью характеризуют результат измерения, т.к.
не полностью характеризуют результат измерения, т.к. 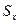 только обозначает границы интервала, в котором может находиться истинное значение, и ничего не говорит о том, с какой вероятностью истинное значение попадает в этот интервал, поскольку неизвестно по какому закону распределены исходные случайные величины. Кроме того, при суммировании погрешностей, представленных точечными оценками, результат может существенно превышать действительное значение.
только обозначает границы интервала, в котором может находиться истинное значение, и ничего не говорит о том, с какой вероятностью истинное значение попадает в этот интервал, поскольку неизвестно по какому закону распределены исходные случайные величины. Кроме того, при суммировании погрешностей, представленных точечными оценками, результат может существенно превышать действительное значение.
Более полное представление дает доверительный интервал. По определению, площадь, ограниченная кривой плотности вероятности, отражает вероятность всех возможных значений случайной погрешности, т.е. 100 % попадания погрешности в интервал ±∞. Эту площадь можно разделить на части вертикальными линиями, абсциссы которых называют квантилями. На рис.2.7 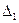 –25% квантиль, т. к. площадь, ограниченная
–25% квантиль, т. к. площадь, ограниченная 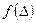 и
и 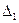 составляет 25% всей площади, тогда
составляет 25% всей площади, тогда 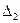 соответствует 75% квантили, а между
соответствует 75% квантили, а между 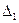 и
и 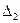 находятся 50% всех возможных значений погрешности. Квантильная оценка погрешности представляется интервалом ±
находятся 50% всех возможных значений погрешности. Квантильная оценка погрешности представляется интервалом ± 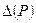 . В этот интервал с заданной вероятностью Р попадает 100×Р процентов всех возможных значений случайной погрешности.
. В этот интервал с заданной вероятностью Р попадает 100×Р процентов всех возможных значений случайной погрешности.
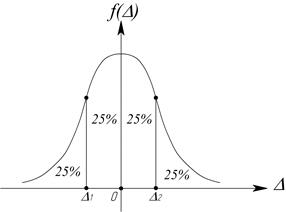
Рис.2.7. Квантильные оценки погрешности
Интервал ± 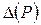 называется доверительным интервалом, а соответствующая ему вероятность Р–доверительной вероятностью.
называется доверительным интервалом, а соответствующая ему вероятность Р–доверительной вероятностью.
Если погрешность распределена по нормальному закону, то доверительные границы случайной погрешности 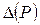 , для доверительной вероятности Р, находят по формуле
, для доверительной вероятности Р, находят по формуле
 (2.8)
(2.8)
где 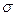 – СКО,
– СКО, 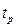 –коэффициент, зависящий от Р (например, для Р=0,95,
–коэффициент, зависящий от Р (например, для Р=0,95, 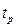 =2).
=2).
Если интервал 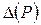 принять равным ±3
принять равным ±3 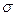 , т. е. коэффициент
, т. е. коэффициент 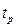 =3, то для нормального закона распределения доверительная вероятность Р=0,997. Это говорит о том, что с вероятностью близкой к единице, все возможные значения погрешности будут принадлежать этому интервалу. Погрешности, не попавшие в интервал ±3
=3, то для нормального закона распределения доверительная вероятность Р=0,997. Это говорит о том, что с вероятностью близкой к единице, все возможные значения погрешности будут принадлежать этому интервалу. Погрешности, не попавшие в интервал ±3 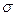 , считают грубыми (браком).
, считают грубыми (браком).
При технических измерениях за доверительную вероятность принимают значение Р=0,95 и только для особо точных и ответственных измерений, связанных, например, с обеспечением безопасности, допускается применять более высокую доверительную вероятность.
При суммировании нескольких случайных погрешностей, заданных доверительными интервалами с разными доверительными вероятностями, возникают сложности, т. к. известно, что доверительный интервал суммы не равен сумме доверительных интервалов и может существенно превышать действительное значение суммарного доверительного интервала.
Из теории вероятностей известно, что суммирование случайных величин имеющих разные законы распределения сводится к композиции этих законов. Задача существенно упрощается, если законы распределения нормальные, а погрешности не коррелированны (независимы). В этом случае суммирование случайных величин осуществляется путем суммирования их дисперсий [2.3]
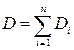 (2.9)
(2.9)
или для СКО
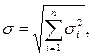 (2.10)
(2.10)
т. е чтобы просуммировать отдельные составляющие случайной погрешности необходимо знать числовые характеристики закона распределения.
Если суммируемые погрешности коррелированны (зависимы), то расчетные соотношения усложняются, а правила суммирования основываются на известных из теории вероятности положениях [2.4]:
· оценка математического ожидания результирующей погрешности определяется алгебраической суммой оценок математических ожиданий составляющих;
· оценка СКО суммарной погрешности имеет вид
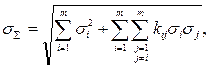 (2.11)
(2.11)
где 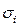 –оценка СКО
–оценка СКО 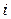 -ой составляющей погрешности; m–число составляющих;
-ой составляющей погрешности; m–число составляющих; 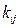 –коэффициент взаимной корреляции между
–коэффициент взаимной корреляции между 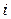 -ой и
-ой и 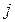 -ой составляющими.
-ой составляющими.
Известно, что коэффициенты взаимной корреляции 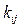 при
при 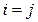 равны единице, а матрица коэффициентов
равны единице, а матрица коэффициентов 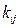 симметрична и диагональна, т.е.
симметрична и диагональна, т.е. 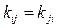 при
при 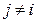 . Тогда
. Тогда
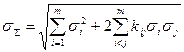 . (2.12)
. (2.12)
Использование этого выражения затруднительно, т.к. точные значения коэффициентов корреляции не всегда известны. В этом случае при расчетах полагают k=0, если случайные составляющие можно считать независимыми (при k<0,7), и k=1, если существует корреляция между суммируемыми составляющими погрешностей (при k>0,7).
Если суммируются нормально распределенные составляющие и известны их доверительные вероятности 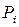 и доверительные интервалы
и доверительные интервалы 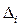 , то можно найти соответствующие СКО
, то можно найти соответствующие СКО
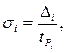 (2.13)
(2.13)
где 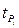 –квантиль соответствующая
–квантиль соответствующая 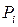 .
.
Если 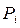 =Р, т. е. доверительные вероятности для всех интервалов
=Р, т. е. доверительные вероятности для всех интервалов 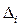 равны,
равны, 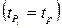 , в соответствии с (2.11), (2.13) можно записать:
, в соответствии с (2.11), (2.13) можно записать:
1) для коррелированных составляющих 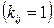
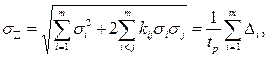 (2.14)
(2.14)
2) для независимых составляющих 
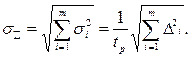 (2.15)
(2.15)
В результате суммирования нормально распределенных составляющих будем иметь результирующую погрешность, распределения которой будет также нормальным. Тогда доверительный интервал суммарной погрешности при доверительной вероятности Р будет равен
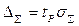 , (2.17)
, (2.17)
а выражение для соответствующих интервальных оценок примет вид:
1) 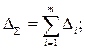 2)
2) 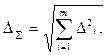 (2.18)
(2.18)
Так как действительные значения 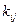 находится в диапазоне от 0 до 1, то простое арифметическое сложение дает завышенное значение
находится в диапазоне от 0 до 1, то простое арифметическое сложение дает завышенное значение  , в то же время геометрическое сложение по второй формуле приводит к заниженному значению, т. е. действительное значение
, в то же время геометрическое сложение по второй формуле приводит к заниженному значению, т. е. действительное значение  находится между ними.
находится между ними.
Очень часто возникает вопрос о том, какими составляющими погрешности можно пренебречь, т. е. о малости этих составляющих. Для этого существует критерий ничтожно малой погрешности. Такой критерий, в частности, необходим при выборе класса точности образцового средства измерений для поверки рабочего СИ.
Один из вариантов критерия гласит [2.4], что если одна величина больше другой на порядок, то меньшей величиной можно пренебречь. Если эти величины не коррелированны, то, согласно [2.15]
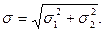
Тогда, с учетом того, что 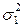 в десять раз больше
в десять раз больше 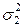 , получим
, получим 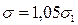 .
.
Таким образом, пренебрежение 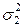 по сравнению
по сравнению 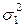 приводит к 5% ошибке при определении СКО суммарной погрешности. Критерий ничтожно малой погрешности для СКО случайной погрешности в этом случае запишется в виде:
приводит к 5% ошибке при определении СКО суммарной погрешности. Критерий ничтожно малой погрешности для СКО случайной погрешности в этом случае запишется в виде:
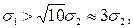 (2.19)
(2.19)
т. е. погрешностью можно пренебречь, если ее СКО или доверительный интервал в 3 раза меньше, чем у оставляемых погрешностей.
2.3. Оценка результатов прямых равноточных многократных
измерений
Результаты многократных наблюдений, получаемых при прямых измерениях величины X , называются равноточными, если они независимые, одинаково распределенные случайные величины, а измерения осуществляются одним наблюдением в одинаковых условиях с помощью одного и того же средства измерений.
Статистическая обработка экспериментального материала выполняется в соответствии с ГОСТ 8.207-76.
Рассмотрим группу 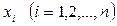 результатов наблюдений.
результатов наблюдений.
Оценкой рассеяния результатов наблюдений в группе относительно среднего 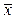 (2.6) будет
(2.6) будет 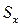 (2.7). Так как число наблюдений в группе ограничено, то повторив заново серию наблюдений такого же объема n, мы получим другое значение
(2.7). Так как число наблюдений в группе ограничено, то повторив заново серию наблюдений такого же объема n, мы получим другое значение 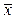 . Повторяя серии n наблюдений и вычисляя каждый раз среднее значение, мы убедимся, что
. Повторяя серии n наблюдений и вычисляя каждый раз среднее значение, мы убедимся, что 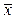 имеет своё рассеяние, числовой характеристикой которого является СКО среднего арифметического
имеет своё рассеяние, числовой характеристикой которого является СКО среднего арифметического 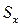 .
.
При обработке многократных наблюдений необходимо учитывать следующие факторы:
· обрабатывается группа наблюдений ограниченного объёма n;
· эта группа может содержать грубые погрешности (промахи);
· результаты наблюдений могут содержать систематическую погрешность;
· распределение случайных погрешностей может отличаться от нормального.
Согласно ГОСТ 8.207-76 обработка результатов наблюдений производится в последовательности:
1. Исключаются известные систематические погрешности из результатов наблюдений.
2. Определяют границы неисключенной систематической погрешности (остатка) результата измерений.
3. Вычисляется среднее арифметическое исправленных результатов наблюдений, которое принимается за результат измерения 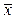 .
.
4. Вычисляется оценка СКО результатов наблюдений 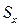 .
.
5. Проверяется наличие в группе наблюдений грубых погрешностей. Если они есть, то их исключают из группы и вновь повторяют вычисление 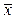 и
и 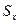 .
.
6. Вычисляют оценку СКО среднего арифметического 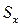 .
.
7. Проверяют гипотезу о принадлежности результатов наблюдений к нормальному закону распределения.
8. Вычисляют доверительные границы случайной погрешности (случайной составляющей погрешности).
9. Вычисляют доверительные границы погрешностей результата измерения.
Основной нормативный документ для выполнения многократных измерений является ГОСТ 8.207-76, а также – ГОСТ 11.002-73 (Прикладная статистика. Правила оценки нормальности результатов наблюдений), ГОСТ 11.004-74 (Прикладная статистика. Правила определения оценок и доверительных границ для параметров нормального распределения).
Среднее арифметическое 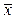 исправленных результатов наблюдений (измерений), принимаемое за результат измерения, вычисляют по формуле
исправленных результатов наблюдений (измерений), принимаемое за результат измерения, вычисляют по формуле
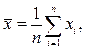 (2.20)
(2.20)
где n - число равноточных наблюдений; 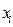 - i-й результат наблюдений.
- i-й результат наблюдений.
Оценку СКО результата наблюдения 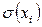 вычисляют по приближенной формуле Бесселя
вычисляют по приближенной формуле Бесселя
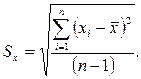 (2.21)
(2.21)
Эта оценка характеризует степень рассеяния результатов наблюдений относительно среднего арифметического 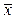 и определяется условиями измерения (метрологическими характеристиками средства измерения, психофизическими качествами экспериментатора и др.).
и определяется условиями измерения (метрологическими характеристиками средства измерения, психофизическими качествами экспериментатора и др.).
В результате измерительного эксперимента получаем выборку 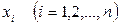 , среди значений которой могут быть значения, существенно отличающихся от других. Принятие решения об исключении (или сохранении) таких значений осуществляют методами статистических гипотез. Для проверки гипотезы о том, что результаты не содержат грубой погрешности (брака), вычисляют величину.
, среди значений которой могут быть значения, существенно отличающихся от других. Принятие решения об исключении (или сохранении) таких значений осуществляют методами статистических гипотез. Для проверки гипотезы о том, что результаты не содержат грубой погрешности (брака), вычисляют величину.
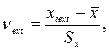 (2.22)
(2.22)
где 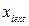 –экстремальные результаты наблюдений.
–экстремальные результаты наблюдений.
Полученные результаты 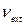 сравнивают с наибольшим значением
сравнивают с наибольшим значением 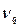 , которое случайная величина
, которое случайная величина 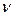 может принять по чисто случайным причинам.
может принять по чисто случайным причинам.
Значение 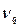 табулированы (см. Приложение 1) для заданной доверительной вероятности
табулированы (см. Приложение 1) для заданной доверительной вероятности 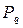 или уровне значимости
или уровне значимости 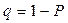 . Если
. Если 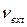 не принадлежит нормальной совокупности, то окажется справедливой зависимость
не принадлежит нормальной совокупности, то окажется справедливой зависимость
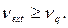 (2.23)
(2.23)
Доверительные границы случайной составляющей погрешности в соответствии со стандартом устанавливают для совокупности  , принадлежащей нормальному распределению. Проверку нормальности, согласно ГОСТ 11.006–74, при n >50, проводят по критериям Пирсона или Мизеса–Смирнова.
, принадлежащей нормальному распределению. Проверку нормальности, согласно ГОСТ 11.006–74, при n >50, проводят по критериям Пирсона или Мизеса–Смирнова.
При 15 < n < 50 используют двойной составной q–критерий.
Критерий 1. Вычисляют отношение
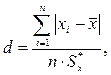 (2.24)
(2.24)
где 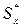 – смещенная оценка СКО, вычисляемая по формуле
– смещенная оценка СКО, вычисляемая по формуле
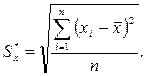
Результаты наблюдений можно считать нормально распределенными, если
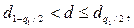 (2.25)
(2.25)
где  и
и 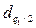 –квантили распределения статистики d (см. Приложение 2); q1– заранее выбранный уровень значимости.
–квантили распределения статистики d (см. Приложение 2); q1– заранее выбранный уровень значимости.
Это условие является необходимым, но не достаточным. Поэтому используют второй критерий.
Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m разностей 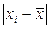 превысили значение
превысили значение 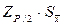 ,
, 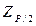 – верхняя квантиль распределения нормированной функции Лапласа, для вероятности Р/2 (см. Приложение 3).
– верхняя квантиль распределения нормированной функции Лапласа, для вероятности Р/2 (см. Приложение 3).
Значение вероятности Р можно определить по выбранному уровню значимости 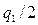 и по числу результатов наблюдений n из соответствующих таблиц.
и по числу результатов наблюдений n из соответствующих таблиц.
В случае, если при проверке нормальности распределения результатов наблюдений хотя бы один из критериев не выполняется, то считают, что данная совокупность не принадлежит нормальному распределению.
При n<15 принадлежность к нормальному закону не проверяется, а доверительные границы случайной погрешности результата измерений определяют лишь в том случае, если есть сведения о нормальности распределения хi.
Доверительные границы 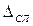 случайной погрешности результата измерения при заданной доверительности вероятности
случайной погрешности результата измерения при заданной доверительности вероятности  вычисляют по формуле
вычисляют по формуле
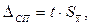
где 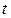 - коэффициент Стьюдента, который определяют из таблиц по числу степеней свободы (n–1) и доверительной вероятности
- коэффициент Стьюдента, который определяют из таблиц по числу степеней свободы (n–1) и доверительной вероятности 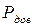 (см. Приложение 4).
(см. Приложение 4).
В ГОСТ 8.207-76 даны рекомендации по определению доверительных границ неисключенной систематической погрешности результата измерений. Она образуется из неисключенных систематических составляющих погрешностей метода, средств измерений, погрешностей поправок и др.
Закон распределения 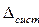 (если нет других сведений) принимают равномерным. В этом случае границы неисключенной систематической погрешности результата измерения
(если нет других сведений) принимают равномерным. В этом случае границы неисключенной систематической погрешности результата измерения 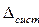 вычисляют по формуле
вычисляют по формуле
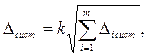 (2.24)
(2.24)
где 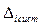 – граница i–й неисключенно
– граница i–й неисключенно
Дата добавления: 2020-10-14; просмотров: 317;











