ЕСЛИ(лог_выражение;значение_если_истина;значение_если_ложь)

Если заданное условие верно (истинно), то выводит значение истина, иначе - ложь.

Функция ЕСЛИ используется при проверке условий для значений и формул.

Лог_выражение — (логическое выражение) - это любое значение выражения, принимающее значения ИСТИНА или ЛОЖЬ.

Примеры:

Логическими выражениями могут быть:

1. A10=100

2. В4=“Информатика”

3. С6<>7 – если значение в ячейке С6 не равно 7

4. С1>=СРЗНАЧ(В1:В8) – если значение в ячейке С1 больше или равно среднему значению данных в диапазоне В1:В8

5. В3<СЕГОДНЯ() – если дата в ячейке В3 по календарю стоит раньше сегодняшней.

Значение_если_истина — это значение, которое будет отображено в ячейке, если лог_выражение равно ИСТИНА. Значение_если_истина может быть формулой.

Значение_если_ложь — это значение, которое возвращается, если лог_выражение равно ЛОЖЬ. Значение_если_ложь может быть формулой.

До 7 функций ЕСЛИ могут быть вложены друг в друга в качестве значений аргументов значение_если_истина и значение_если_ложь для конструирования более сложных проверок (примеры см. ниже).

Примеры

1) =ЕСЛИ(В10>=0;СУММ(С1:С10);СУММ(Е1:Е10)) Результат: формула приводит к вычислению суммы диапазона С1:С10, если значение в ячейке В10 не отрицательно. В противном случае вычисляется сумма диапазона Е1:Е10.

2) Допускается также применение вложенных функций ЕСЛИ. Например: =ЕСЛИ(В10>0; «Прибыль»;ЕСЛИ(В1О<О; «Убыток»; «Ноль») Результат: приведенная формула выводит слово «Прибыль» в случае, если значение ячейки В10 положительно, и слово «Убыток», если значение ячейки отрицательно. Если ячейка содержит нулевое значение или пуста, формула выведет текст «Ноль».

3) Чтобы подсчитать корни квадратного уравнения ax²+bx+c=0 можно составить формулы, например, как на рисунке 4.3. Напомним формулы для дискриминанта и корней ,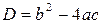

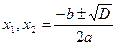
4) Задача: Обучаясь по рейтинговой системе и набрав определенное количество баллов по предмету, студенту выставляется соответствующая оценка. Необходимо составить формулу для выставления оценки в зависимости от набранного количества баллов, если рейтинг по дисциплине следующий: 78 – 85 баллов - «5»; 69 – 77 баллов - «4»; 60 – 68 баллов - «3», менее 60 баллов - «2».

Решение данной задачи может быть оформлено, например, как на рисунке 4.4. В ячейке С2 вводится формула с функцией ЕСЛИ с вложенными двумя функциями ЕСЛИ.

Функция И

=И(логическое_выражение1; логическое_выражение2;...)

Эта функция может содержать до 30 аргументов, в качестве которых выступают логические выражения или ссылки на ячейки, содержащие логические значения.

Выдает одно из двух значений:

ИСТИНА если все аргументы принимают значения ИСТИНА; ЛОЖЬ –если хотя бы один из них принимает значение ЛОЖЬ. Примеры приведены после описания функции ИЛИ.

Функция ИЛИ

=ИЛИ(логическое_выражение1; логическое_выражение2;...)

Значение ИСТИНА в том случае, если хотя бы один аргумент функции принимает значение ИСТИНА.

Примеры

Рисунок 4.5

(в формулах подчеркнуты истинные выражения, остальные являются ложными)

Логические функции часто используются в комбинации друг с другом. Например, в функцию ЕСЛИ в качестве логического выражения можно вставить функцию И, с помощью которой перед выполнением какого-либо действия осуществляется проверка соблюдения сразу нескольких условий.

В качестве примера приведем список результатов экзаменов группы учащихся. С помощью логических функций можно автоматически указать, кто из них по результатам сессии будет получать стипендию, переведен на другой курс или будет отчислен.

В представленной таблице (рис.4.6) в ячейку F3 помещена следующая формула: =ЕСЛИ(И(B3>3;C3>3;D3>3;E3>3);"Стипендия";""). Она проверяет, все ли оценки за экзамены выше тройки. При положительном ответе в ячейке выводится слово «Стипендия», в противном случае - ячейка остается пустой.

А в ячейке G3 помещена другая формула, которая проверяет, нет ли среди сдавших экзамены тех, кто получил хотя бы одну оценку ниже тройки:

=ЕСЛИ(ИЛИ(B3<3;C3<3;D3<3;E3<3);"Отчислен";"Переведен")

При положительном ответе в ячейке выводится сообщение «Отчислен», при отрицательном - «Переведен».