Объект и средства исследования

Объектом исследования является последовательная цепь, включающая в себя индуктивную катушку с постоянными параметрами R, L, и батарею конденсаторов, ёмкость которой C меняется при помощи переключателей П2. Ёмкость батареи равна сумме емкостей параллельно включенных в неё конденсаторов. Элементы исследуемой цепи смонтированы на плате № 10 передней панели стенда.

В качестве электроизмерительных приборов применяется многопредельный миллиамперметр типа Э-З77 и электронный вольтметр (цифровой или стрелочный). Источником питания исследуемой цепи является одна из фаз трёхфазного источника.

1. Собрать электрическую цепь в соответствии со схемой, изображенной на рисунке 5.П.1 протокола испытаний. После проверки цепи преподавателем подать на неё напряжение, включив тумблер В1 (3 ~36 B) на центральной панели стенда в положение «Вкл».

2. Установить в цепи режим резонанса напряжений. Для этого необходимо постепенно увеличивать ёмкость батареи конденсаторов, начиная с минимального значения, с помощью переключателей П2, наблюдая по амперметру за величиной тока цепи I. Достижение током I максимально возможного значения свидетельствует о наступлении режима резонанса напряжений. Записать значения ёмкости, тока и напряжений при резонансном режиме в третью строку таблицы 5.П.1 протокола испытаний.

3. Провести измерения тока и напряжений в цепи при двух меньших и двух бóльших значениях ёмкости батареи конденсаторов, чем в резонансном режиме. Результаты измерений записать соответственно в первую, вторую и четвёртую, пятую строки таблицы 5.П.1 (по возрастанию ёмкости). При проведении опытов нужно стремиться к тому, чтобы они охватывали как можно больший интервал изменения ёмкости батареи (примерно от 20 до 90 мкФ).

4. Выключить тумблер В1. Согласовать полученные результаты с преподавателем. Разобрать цепь.

Исследование линейной разветвлённой
электрической цепи синусоидального тока

Резонансом называется такой режим работы цепи, включающей в себя индуктивные и ёмкостные элементы, при котором её входная проводимость (входное сопротивление) вещественна (т. е. имеет только активную составляющую). Следствием этого является совпадение по фазе тока на входе цепи с входным напряжением.

В электрических цепях различают два вида резонанса: резонанс напряжений (при последовательном соединении L и C элементов) и резонанс токов (при параллельном соединении L и C элементов).

В настоящей лабораторной работе исследуется разветвлённая электрическая цепь, состоящая из параллельно соединённых катушки индуктивности и конденсатора, подключенная к источнику синусоидального напряжения. Схема цепи представлена на рисунке 6.1.

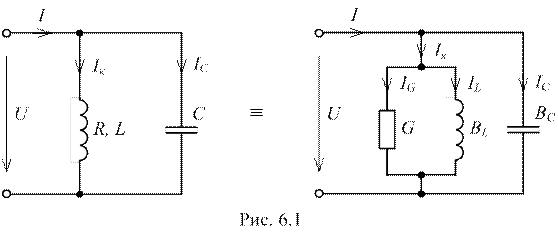
Так как реальная катушка индуктивности обладает кроме реактивного ещё и активным сопротивлением, её целесообразно представить в виде эквивалентной схемы замещения. В отличие от цепи с последовательным соединением катушки и конденсатора в данном случае удобнее воспользоваться параллельной схемой замещения катушки индуктивности, которая представляет собой параллельное соединение идеальных активного и индуктивного элементов с проводимостями G и B_L соответственно (рис. 6.1). Пренебрегая (в отличие от катушки) несущественными потерями активной энергии в конденсаторе, будем считать его идеальным ёмкостным элементом с ёмкостной проводимостью В_C (рис. 6.1).

В соответствии с законом Ома полная проводимость цепи, приведённой на рисунке 6.1, запишется как

,

где: U и I – действующие значения напряжения и тока цепи.

Общая проводимость цепи, состоящей из параллельного соединения активного, индуктивного и ёмкостного элементов, будет являться суммой проводимостей этих элементов. Однако, поскольку сопротивления (а, следовательно, и проводимости) указанных элементов определяются различными факторами (соответственно электрическим сопротивлением металла и сопротивлениями движению тока, обусловленными магнитным и электрическим полями), вводится понятие комплексной проводимости 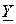(аналогично комплексному сопротивлению ), представляющей общую проводимость активных и реактивных элементов в виде комплексного числа. При этом активная проводимость G рассматривается в качестве вещественной части данной комплексной проводимости, а реактивная проводимость B, определяемая разницей ёмкостной B_C и индуктивной B_L проводимостей (B=B_C–B_L), – в качестве мнимой части:

.

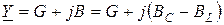Таким образом, активная и реактивная проводимости с двух качественно разных сторон характеризуют общую проводимость цепи. Они откладываются по различным осям на комплексной плоскости, благодаря чему складываются не как скаляры, а как вектора. Величины B_C и B_L откладываются по мнимой оси в противоположных направлениях. Вектор напряжения при построении векторной диаграммы на комплексной плоскости для параллельной цепи, как правило, откладывается по действительной оси, а вектора токов на ёмкостном и индуктивном элементах при их углах к напряжению φ_C= +90° и φ_L= –90° соответственно – в положительном и отрицательном направлениях мнимой оси соответственно. По этой причине и реактивные проводимости B_C и B_L, обуславливающие указанные токи, откладываются в положительном и отрицательном направлениях мнимой оси соответственно.

В связи с вышесказанным соотношения активной, реактивной и полной проводимостей характеризуются треугольником проводимостей (рис. 6.2), откуда вытекают следующие зависимости:

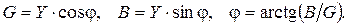
Вернувшись к представлению индуктивной катушки в виде схемы замещения с параллельным соединением активного и индуктивного элементов, определим параметры этих элементов через параметры катушки R и X_L. Полное сопротивление катушки при последовательном соединении R и L элементов: 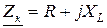. Тогда полная проводимость катушки:

.

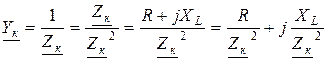В полученном выражении имеется сумма двух составляющих проводимости: и 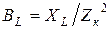. Следовательно, эти составляющие можно рассматривать как проводимости двух параллельно включенных ветвей с общей проводимостью .

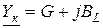Проводимость ветви с ёмкостным элементом: .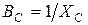

Полный ток цепи, приведённой на рисунке 6.1, определяется (аналогично полной проводимости) векторной суммой токов параллельно соединённых ветвей (по первому закону Кирхгофа):

.

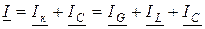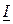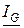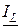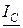Величины , , и связаны между собой, как стороны треугольника токов (рис. 6.3), подобного треугольнику проводимостей. Треугольник токов получается из треугольника проводимостей, домножением сторон последнего на напряжение U. Вектор тока на резистивном элементе 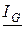(активная составляющая 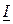) совпадает по направлению с вектором напряжения 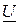, вектор тока на ёмкостном элементе 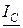(ёмкостная составляющая 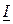) опережает вектор напряжения на 90°, а вектор тока на индуктивном элементе 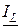(индуктивная составляющая 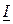) отстаёт от вектора напряжения на 90°. Из векторной диаграммы токов и напряжения (рис. 6.3) следует:

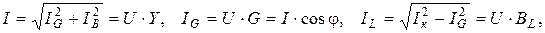
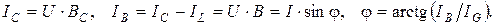
Домножив стороны треугольника проводимостей на квадрат напряжения или домножив стороны треугольника токов на напряжение, можно получить треугольник мощностей (рис. 6.4).

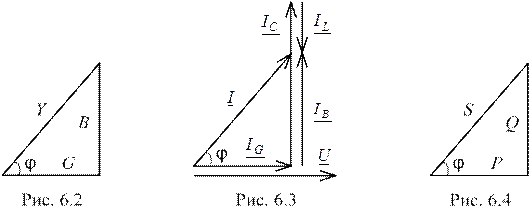
Для полной S, активной P и реактивной Q мощностей справедливы следующие соотношения:

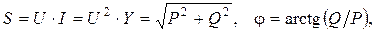
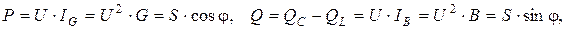
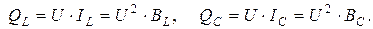
В электрической цепи (рис. 6.1) возможны три различных соотношения параметров B_C и B_L:

а) B_C>B_L, тогда I_C>I_L, вектор 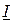опережает вектор 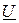на угол φ, цепь носит ёмкостный характер (рис. 6.5–а);

б) B_C<B_L, тогда I_C<I_L, вектор 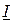отстаёт от вектора 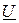на угол φ, цепь носит индуктивный характер (рис. 6.5–б);

в) B_C=B_L, тогда I_C=I_L, вектор 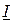совпадает по направлению с вектором 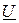(φ=0), цепь работает в режиме резонанса и носит активный характер (рис. 6.5–в).

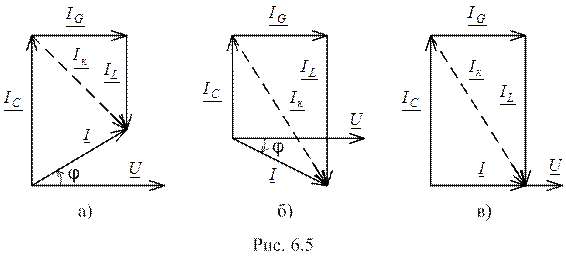
Режим работы параллельной цепи синусоидального тока, при котором напряжение и общий ток совпадают по фазе, что соответствует совпадению по направлению векторов и 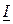на векторной диаграмме, называется резонансом токов.

Так как в режиме резонанса реактивная проводимость всей цепи равно нулю (B=B_C–B_L=0), то и реактивные составляющие всех величин на входе цепи (тока, мощности) тоже равны нулю.

Условием резонанса является равенство ёмкостной и индуктивной проводимостей параллельных ветвей:

или ,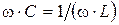

откуда следует, что резонанс наступает при частоте

.

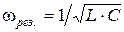Таким образом, резонанс в цепи может быть получен за счёт изменения одного из следующих параметров: индуктивности катушки L, ёмкости конденсатора C или частоты питающего напряжения f (ω=2∙π·f). Кроме того, величина в схеме на рисунке 6.1 зависит от активного сопротивления катушки R, следовательно, последнее тоже влияет на достижение режима резонанса. В данной работе резонанс токов достигается с помощью изменения ёмкости конденсатора.

Так как режим резонанса наступает при B=0, полная проводимость цепи с параллельным соединением L и C элементов в этот момент достигает наименьшего значения Y_рез.=G, что приводит к существенному уменьшению тока, который достигает минимального значения I_рез:

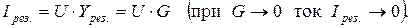
Токи I_C и I_L имеют одинаковые действующие значения и противоположны по фазе, т. е. на векторной диаграмме векторы 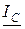и 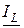имеют равную длину и направлены в противоположные стороны.

В режиме резонанса коэффициент мощности цепи 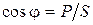, который показывает какую часть от полной мощности составляет активная, достигает своего максимального значения. Это происходит по причине того, что реактивные мощности на ёмкостном и индуктивном элементах равны (Q_C=Q_L), из чего следует равенство нулю реактивной мощности цепи (Q=Q_C–Q_L=0) и равенство полной и активной мощностей S_рез.=P.

Физическая сущность резонанса заключается в периодическом обмене энергией (реактивной) между магнитным полем индуктивной катушки и электрическим полем конденсатора, причём сумма энергий полей остается постоянной (источник питания цепи в этом обмене реактивной энергией не участвует).

Исследование трёхфазной электрической цепи
с активной нагрузкой, соединённой по схеме «звезда»

Трёхфазная электрическая цепь включает в себя трёхфазный источник и трёхфазный потребитель электроэнергии, соединённые проводами.

Источник трёхфазной электрической энергии может быть представлен в виде совокупности трёх однофазных источников синусоидальных ЭДС (E_A, E_B, E_C) одинаковой частоты ω и амплитуды E_m, сдвинутых друг относительно друга по фазе на угол ψ=2∙π / m=120° (m=3 – количество фаз), т. е. на 1/3 периода. Такие ЭДС образуют симметричную трёхфазную систему, а их мгновенные значения записываются следующим образом:

.

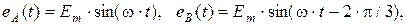
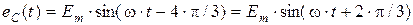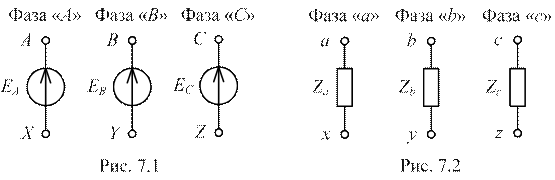
Каждый из записанных однофазных источников энергии является фазой трёхфазного источника (не следует путать данное понятие фазы с начальной фазой синусоидальной величины). Как правило, трёхфазные ЭДС вырабатываются в трёхфазных обмотках электрических машин. В зависимости от направления ЭДС различают начала и концы фаз генератора (соответственно начала и концы обмоток трёхфазных электрических машин): ЭДС в каждой фазе направлена от конца фазы (обозначение «X», «Y», «Z») к началу (обозначение «A», «B», «C»). Началом обмотки (фазы) генератора называется зажим, через который ток поступает во внешнюю цепь в положительном направлении. По буквенным обозначениям начал фаз именуются и сами фазы: «A», «B», «C». Обозначения фаз генератора приведены на рисунке 7.1.

Трёхфазный потребитель энергии аналогичным образом может быть представлен в виде совокупности трёх однофазных потребителей (Z_A, Z_B, Z_C), каждый из которых является фазой трёхфазной нагрузки. Начала и концы фаз потребителя, а также сами фазы, обозначаются теми же буквами, что и соответствующие фазы генератора, но только не прописными, а строчными (рис. 7.2).

Существуют две основные схемы соединения фаз трёхфазного генератора или приёмника: схема «звезда» (обозначение «Y») и схема «треугольник» (обозначение «Δ»).

При использовании схемы соединения «звезда» концы фаз генератора «X», «Y», «Z» или потребителя «x», «y», «z» соединяются в соответствующие общие точки, называемые нейтральными точками («N» – для генератора, «n» – для потребителя), а соответствующие начала фаз генератора «A», «B», «C» и приёмника «a», «b», «c» соединяются линейными проводами A–a, B–b, C–c (рис. 7.3). Нейтральные точки генератора и приёмника при необходимости соединяются нейтральным проводом N–n. При наличии нейтрального провода трёхфазная цепь называется четырёхпроводной, а при его отсутствии – трёхпроводной.

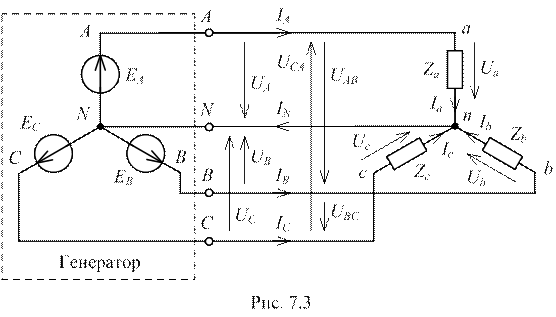
Напряжение между началом и концом каждой фазы генератора или приёмника называется фазным напряжением генератора или приёмника соответственно и обозначается U_A, U_B, U_C – для генератора, U_a, U_b, U_c – для приёмника (рис. 7.3).

Напряжение между началами двух разных фаз или между двумя линейными проводами называется линейным напряжением (U_AB, U_BC, U_CA на рисунке 7.3).

Токи, протекающие по фазам приёмника (I_a, I_b, I_c) или генератора (I_A, I_B, I_C), называются фазными токами приёмника или генератора соответственно, а токи, проходящие в линейных проводах, (обозначаются как и фазные токи генератора) называются линейными токами. Поскольку при соединении «звездой» фаз генератора или приёмника, каждая фаза включается последовательно с соответствующим линейным проводом, фазные токи равны линейным (для схемы на рисунке 7.3: I_A=I_a, I_B=I_b, I_С=I_с). Общее обозначение для всех фазных токов «I_ф», а для линейных – «I_л». Тогда, для схемы соединения «звезда» можно записать: I_л=I_ф.

На основании первого закона Кирхгофа (рис. 7.3) векторная сумма фазных токов равна току в нейтральном проводе:

.

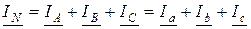Если пренебречь внутренними сопротивлениями ЭДС фаз генератора, то фазные напряжения генератора U_A, U_B, U_C будут равны соответствующим фазным ЭДС E_A, E_B, E_C:

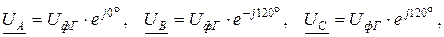
где: U_фГ – действующее значение фазного напряжения генератора (в симметричной системе). В соответствии со вторым законом Кирхгофа при соединении «звездой» линейные напряжения выражаются через фазные напряжения генератора следующим образом (рис. 7.3):

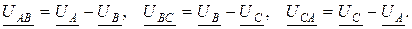
На рисунке 7.4 представлена векторная топографическая диаграмма фазных напряжений генератора и линейных напряжений, которые образуют жёсткую симметричную систему, не зависящую от нагрузки. Из диаграммы следует, что действующие значения всех линейных напряжений одинаковы (общее обозначение линейных напряжений «U_л»):

,

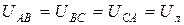и что фазные напряжения генератора и линейные напряжения находятся в соотношении

.

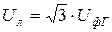При наличии нейтрального провода потенциал точек «N» и «n» одинаковы и, следовательно, фазные напряжения приёмника равны фазным напряжениям генератора: U_A=U_a, U_B=U_b, U_C=U_c.

Нагрузка, подключаемая к трёхфазной сети, может быть симметричной и несимметричной. При симметричной нагрузке комплексные сопротивления всех фаз приёмника одинаковы: 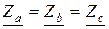. Вследствие этого действующие значения токов в фазах одинаковы (I_a=I_b=I_c), а векторы токов направлены под углом 120° друг к другу. Векторная диаграмма напряжений и токов для симметричной нагрузки представлена на рисунке 7.5. Если в качестве приёмников используются резисторы, векторы токов в фазах приёмника совпадают по направлению с соответствующими векторами фазных напряжений приёмника и генератора. Ток в нейтральном проводе, определяемый векторной суммой фазных токов будет равен нулю, так как векторы фазных токов образуют симметричную тройку векторов. Таким образом, при симметричной нагрузке надобность в нейтральном проводе отпадает.

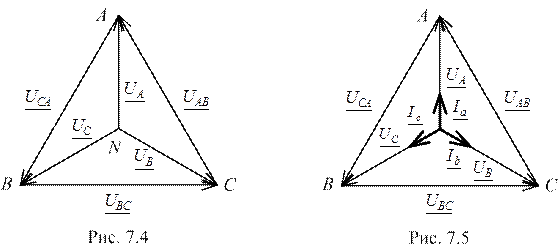
При несимметричной нагрузке (когда нарушается условие 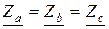) режим работы цепи будет различным в зависимости от наличия или отсутствия нейтрального провода. В четырёхпроводной цепи, т. е. с нейтральным проводом, обеспечивается симметрия фазных напряжений приёмника (общее обозначение фазных напряжений приёмника U_фП) вследствие их равенства фазным напряжениям генератора, следовательно

.

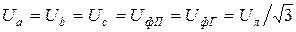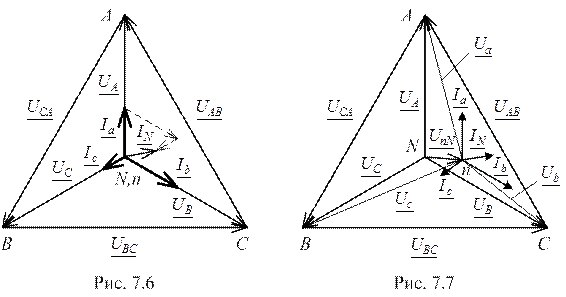
Векторы фазных токов не будут симметричными вследствие различия сопротивлений в фазах, что приводит к возникновению тока в нейтральном проводе. Векторная диаграмма напряжений и токов для четырёхпроводной цепи при несимметричной нагрузке приведена на рисунке 7.6. Векторы фазных токов совпадают с векторами соответствующих фазных напряжений вследствие активного характера нагрузки. Ток I_N в нейтральном проводе строится как векторная сумма фазных токов.

Если при несимметричной нагрузке отключить нейтральный провод, то в полученной трёхпроводной цепи нарушится равенство потенциалов нейтральных точек генератора и приёмника. В результате, между ними возникнет разность потенциалов U_nN, называемая напряжением смещения нейтрали. Векторная диаграмма напряжений и токов для трёхпроводной цепи при несимметричной нагрузке представлена на рисунке 7.7. Положение нейтральной точки приёмника на векторной топографической диаграмме может быть определено графически по экспериментальным значениям фазных напряжений приёмника. Для этого из вершин треугольника АВС, образуемого векторами линейных напряжений, необходимо провести дуги радиусами, равными в выбранном масштабе фазным напряжениям приёмника U_a, U_b, U_c. Точка пересечения дуг укажет положение точки «n».

Векторы, соединяющие точку «n» с вершинами треугольника, являются векторами фазных напряжений приёмника 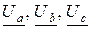. Они связаны с векторами фазных напряжений генератора 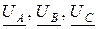следующими соотношениями:

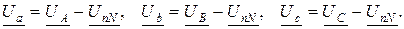
Векторы токов совпадают по фазе с напряжениями 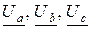поскольку нагрузка является активной. При этом в соответствии с первым законом Кирхгофа

.

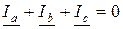Как следует из векторной диаграммы (рис. 7.7) действующие значения напряжений в разных фазах нагрузки неодинаковы, что неблагоприятно сказывается на работе потребителей электрической энергии. По этой причине несимметричную нагрузку включают только в четырёхпроводную цепь и в нейтральный провод не ставят аппаратов защиты (например, предохранителей), способных вызвать его разрыв.

Объектом исследования является трёхфазная цепь, состоящая из источника питания и нагрузки, соединённой по схеме «звезда». Источником питания служит трёхфазный четырёхпроводная сеть с линейным напряжением 36 В. Выходные гнёзда источника «А», «В», «С», «N» расположены на центральной панели стенда, питание на них подаётся включением трёхполюсного выключателя В1.

В качестве трёхфазной нагрузки используются три резистора с регулируемой величиной сопротивления, смонтированные в правой части центральной панели на платах № 8, № 9, № 10. Для выполнения электроизмерений применяются многопредельные миллиамперметры Э-377 и цифровой или стрелочный электронный вольтметр.

Исследование трёхфазной электрической цепи с активной
нагрузкой, соединённой по схеме «треугольник»

Трёхфазная электрическая цепь включает в себя трёхфазный источник и трёхфазный потребитель энергии, соединённые проводами.

Источник трёхфазной электроэнергии может быть представлен в виде совокупности трёх однофазных источников синусоидальных ЭДС одинаковой частоты ω и амплитуды E_m, сдвинутых друг относительно друга по фазе на угол ψ=2∙π / m=120° (m=3 – количество фаз):

Такие ЭДС образуют симметричную трёхфазную систему. Каждый из однофазных источников энергии называется фазой трёхфазного источника (генератора). ЭДС в каждой фазе направлена от конца фазы («X», «Y», «Z») к началу («A», «B», «C»). Началом фазы генератора называется зажим, через который ток поступает во внешнюю цепь в положительном направлении. По буквенным обозначениям начал фаз именуются и сами фазы: «A», «B», «C».

Трёхфазный потребитель энергии аналогичным образом может быть представлен в виде совокупности трёх однофазных потребителей, каждый из которых называется фазой трёхфазной нагрузки. Начала и концы фаз потребителя, а также сами фазы, обозначаются теми же буквами, что и соответствующие фазы генератора, но только не прописными, а строчными.

Существуют две основные схемы соединения фаз трёхфазного генератора или приёмника: схема «звезда» («Y») и схема «треугольник» («Δ»).

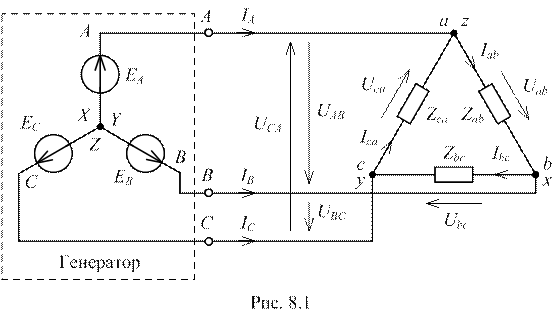
При использовании схемы «треугольник» конец каждой предыдущей фазы соединяется с началом следующей, образуя замкнутый контур, а точки соединения фаз подключаются к линейным проводам (А–а, В–b, С–с), связывающим источник энергии с потребителем (рис. 8.1).

Напряжения U_AB, U_BC, U_CA между линейными проводами или между началами двух разных фаз называются линейными напряжениями (U_л). Для симметричного трёхфазного источника система линейных напряжений является симметричной, благодаря чему на векторной топографической диаграмме векторы линейных напряжений образуют равносторонний треугольник (рис. 8.2, 8.3).

Напряжения (U_ab, U_bc, U_ca) между началом и концом каждой фазы приёмника называются фазными напряжениями приёмника (U_фП). Поскольку при соединении «треугольником» каждая фаза нагрузки включена между парой линейных проводов, фазные напряжения нагрузки равны линейным напряжениям: U_фП=U_л.

Токи, протекающие по фазам приёмника (I_ab, I_bc, I_ca), называются фазными токами приёмника (I_фП), а токи, проходящие в линейных проводах, (I_A, I_B, I_C) называются линейными токами (I_л). В соответствии с первым законом Кирхгофа в схеме соединения «треугольник» комплексные значения фазных и линейных токов связаны следующими соотношениями:

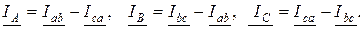
Трёхфазная нагрузка может быть симметричной и несимметричной. Нагрузка является симметричной, если комплексные сопротивления всех фаз одинаковы: . В противном случае нагрузка несимметрична. Вследствие равенства действующих значений фазных напряжений (U_ab=U_bc=U_ca) действующие значения токов в фазах симметричной нагрузки одинаковы: I_ab=I_bc=I_ca=I_фП.

При построении векторной диаграммы напряжений и токов сначала
строится равносторонний треугольник из векторов линейных напряжений 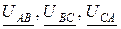, равных фазным напряжениям нагрузки (рис. 8.2, 8.3).

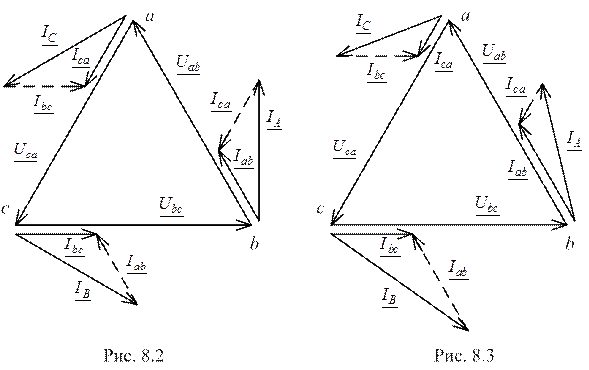
Начала векторов фазных токов 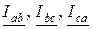совмещают с началами векторов соответствующих фазных (линейных) напряжений. Угол φ сдвига фаз между соответствующими фазными векторами тока и напряжения определяется характером нагрузки. Для активной нагрузки векторы тока и напряжения совпадают по направлению, т. е. φ=0. Векторы линейных токов 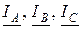строят, используя вышеприведённые соотношения, как сумму соответствующих векторов фазных токов.

На рисунках 8.2, 8.3 приведены векторные топографические диаграммы напряжений и совмещённые с ними векторные диаграммы токов для симметричной (рис. 8.2) и несимметричной (рис. 8.3) активной нагрузки. Из векторной диаграммы на рисунке 8.2 следует, что для симметричной нагрузки наряду с равенством действующих значений фазных токов будет выполняться также равенство действующих значений линейных токов, т. е. I_A=I_B=I_C=I_л. При этом соотношение действующих значений фазного и линейного токов запишется как

.

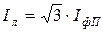Векторная диаграмма на рисунке 8.3, построенная для несимметричной нагрузки (I_ca<I_bc<I_ab), отличается неравенством треугольников токов, откуда следует, что действующие значения линейных токов, так же, как и фазных, будут неодинаковыми.

Объектом исследования является трёхфазная цепь, состоящая из источника питания и нагрузки, соединённой по схеме «треугольник». Источником питания служит трёхфазный сеть с линейным напряжением 36 В. Выходные гнёзда источника «А», «В», «С» (гнездо «N» в данной работе не задействовано) расположены на центральной панели стенда, питание на них подаётся включением трёхполюсного выключателя В1.

В качестве трёхфазной нагрузки используются три резистора с регулируемой величиной сопротивления, смонтированные в правой части центральной панели на платах № 8, № 9, № 10. Для выполнения электроизмерений применяются многопредельные миллиамперметры Э-377 и цифровой или стрелочный электронный вольтметр.