Примеры решения задач моделирования на GPSS

Пример 1. Моделирование непрерывной случайной величины распределённой по экспоненциальному закону с l = 0.1.

10 SIMULATE

20 EXPON FUNCTION RN1, C24

30 0.0/.1,.104/.2,.222/.3,.365/.4,.509/.5,.69

.6,.915/.7,1.2/.75,1.38/.8,1.6/.84,1.83/.88,2.12

.9,2.3/.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5

.98,3.9/.99,4.6/.995,5.3/.995,6.2/.999,7.01.9997,8.0

40 GENERATE 10,FN$EXPON

50 MARK1

60 TABULATE XTIME

70 TERMINATE 1

80 XTIME TABLE P1,0,2,100

90 START 200

100 END

Модель включает 4 блока, выполняющие следующие функции:

40 - генерирование транзакта;

50 - присвоение параметру 1 транзакта значения, равного текущему значению часового времени;

60 - уничтожение транзакта;

10 - признак, необходимый для прогона модели;

20 - описание функции (EXPON - метка, RN1 - генератор случайной функции, число пар координат-24);

30 - задание значений пар координат функции;

80 - определение таблицы; XTIME - метка, табулируемой величиной является Р1 значение параметров последовательных транзактов, верхний предел первого интервала равен 0, ширина интервала - 2, общее число интервалов - 100;

90 - признак ввода данных, необходимый для выполнения моделирования; прогон модели должен завершится после прохождения через неё 200 транзактов;

100 - признак конца программы.

Пример 2. Составить модель композиции двух случайных величин X₁ и X₂ имеющих экспоненциальные распределения с параметрами l₁ и l₂ (Х= X₁ + X₂), удовлетворяющих обобщённому закону Эрланга 1-ого порядка: g(t)= l₁l₂(e^-l1- e^-l2)/(l_1­-l₂).

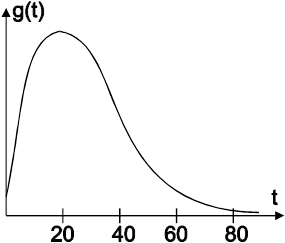
Рис. 10.1. К задаче моделирования композиции 2-х случайных величин.

10 SIMULAT

20 EXPON FUNCTION RN1, C24

30 0.0/.1,.104/.2,.222/.3,.365/.4,.509/.5,.69

.6,.915/.7,1.2/.75,1.38/.8,1.6/.84,1.83/.88,2.12

.9,2.3/.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5

.98,3.9/.99,4.6/.995,5.3/.995,6.2/.999,7.01.9997,8.0

40 GENERATE 0,0,,1

50 ASSIGN 1,K500

60 INPUT ADVANCE 10,FN$EXPON

70 ADVANCE 20, FN$EXPON

80 TABULATE XTIME

90 LOOP 1,INPUT

100 TERMINATE 1

110 XTIME TABLE M1,0,5,100

120 START 1

130 END.

Функции блоков:

40 - генерирование 1-ого транзакта в момент времени t=0;

50 - присвоение параметру 1 значения, равного 500;

60 - моделирование экспоненциального распределённых временных интервалов с параметром l₁;

70 - моделирование экспоненциального распределённых временных интервалов с параметром l₂;

80 - формирование таблиц частот XTIME для суммарных интервалов;

90 - контроль числа прохождений транзактов через сегмент блоков, начинающийся с блока INPUT;

100 - уничтожение транзакта.

Пример 3. Моделирование однолинейной системы с пуассоновским входящим потоком с параметром l = 0.1 1/сек. И экспоненциальным временем обслуживания с параметром m = 0.2 1/сек.

10 SIMULATE

20 LINE EQU 1

30 EXPON FUNCTION RN1,C24

40 0.0/.1,.104/.2,.222/.3,.365/.4,.509/.5,.69

.6,.915/.7,1.2/.75,1.38/.8,1.6/.84,1.83/.88,2.12

.9,2.3/.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5

.98,3.9/.99,4.6/.995,5.3/.995,6.2/.999,7.01.9997,8.0

50 GENERATE 10, FN$EXPON

60 ASSIGN 1,LINE

70 QUEUE O1

80 SEIZE LINE

90 DEPART O1

100 ADVANCE 5,FN$EXPON

110 RELEASE LINE

120 TABULATE XTIME

130 TERMINATE 1

140 XTIME TABLE M1,0,10,100

150 START 500

160 END.

9 блоков: 50 - генерирование транзактов;

60 - назначение параметру 1 транзакта номера, соответствующего прибору LINE;

70 - вхождение транзакта в очередь на прибор;

80 - занятие прибора;

90 - выход из очереди;

100 - моделирование обслуживания;

110 - освобождения прибора;

120 - формирование таблицы частот XTIME для времени прохождения транзакта;

130 - уничтожение транзакта;

20 - назначение величины 1 переменной LINE.

Пример 4. Моделирование работы однолинейной системы, имеющей 3 Пуассоновских потока требований с относительными приоритетами и параметрами l₁=0.01 1/сек., l₂=0.04 1/сек., l₃=0.05 1/сек. Экспоненциальный закон обслуживания m₁=0.2 1/сек.

10 SIMULATE

20 LINE EQU 1

30 EX FUNCTION

40 0.0/.1,.104/.2,.222/.3,.365/.4,.509/.5,.69

.6,.915/.7,1.2/.75,1.38/.8,1.6/.84,1.83/.88,2.12

.9,2.3/.92,2.52/.94,2.81/.95,2.99/.96,3.2/.97,3.5

.98,3.9/.99,4.6/.995,5.3/.995,6.2/.999,7.01.9997,8.0

50 GENERATE 100, FN$EX,,,3

60 TRANSFER ,INPUT

70 GENERATE 25, FN$EX,,,2

80 TRANSFER ,INPUT

90 GENERATE 20, FN$EX,,,1

100 INPUT ASSIGN 1,LINE

110 QUEUE LINE

120 SEIZE LINE

130 DEPART LINE

140 ADVANCE 5,FN$EX

150 RELEASE LINE

160 TERMINATE 1

170 START 1000

60, 80 - безусловная передача транзактов;

50, 70, 90 - генерирование транзактов с приоритетами 3, 2, 1.

Планирование машинных экспериментов с моделями систем.

11.1 Методы планирования эксперимента на модели.

Основная задача планирования машинных экспериментов заключается в получении необходимой информации об исследуемой системе при ограниченных ресурсах (затраты машинного времени, памяти и т.п.). К числу частных задач, решаемых при планировании машинных экспериментов, относятся задачи уменьшения затрат машинного времени на моделирование, уменьшения погрешности результатов моделирования, проверки адекватности модели и т.п.

Эффективность машинных экспериментов существенно зависит от выбора плана эксперимента, т.к. именно план определяет объём и порядок проведения вычислений на ЭВМ, приёмы накопления и статистической обработки результатов моделирования системы. Поэтому основная задача планирования машинных экспериментов с моделью формируется следующим образом: необходимо получить об объёме моделирования, заданном в виде моделирующего алгоритма (программы) при минимальных или ограниченных затратах машинных ресурсов на реализацию процесса моделирования.

Таким образом, при машинном моделировании необходимо не только рационально планировать и проектировать саму модель системы, но и процесс её использования, т.е. проведения с ней эксперимента.

При планировании машинных экспериментов возникает целый ряд проблем, взаимно связанных как с особенностью функционирования моделируемого объекта, так и с особенностью машинной реализации модели и обработки результатов эксперимента. В первую очередь к таким относятся проблемы построения плана машинного эксперимента, стохастической сходимости результатов, ограниченности машинных ресурсов, уменьшения дисперсии оценок, полученных на машинной модели и т.д.

Рассмотрим основные понятия теории планирования эксперимента. В планировании эксперимента различают входные (изогенные) и выходные (эндогенные) переменные: х₁, х₂,…, х_к; y_1, y₂…, y_e. Входные переменные в ТПЭ называют факторами а выходные — реакциями. Каждый фактор x_i, i=1,2,…,k может принимать в эксперименте одно или несколько значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов.

Каждому фиксированному набору уровню факторов соответствует определённая точка в многомерном пространстве, называемая факторным пространством. Эксперименты не могут быть реализованы во всех точках факторного пространства, а лишь в принадлежащих допустимой области, как это например оказано для случая двух факторов Х₁ и Х₂ на рисунке (см. ниже рис. 11.1.).

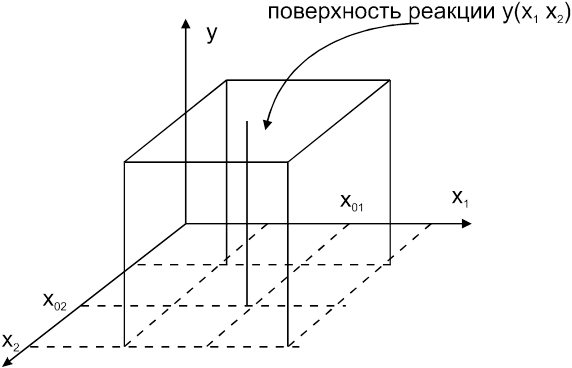
Рис. 11.1. Геометрическое представление поверхности реакции.

Реакцию (отклик) системы можно представить в виде зависимости: y_l=Y_l(x₁, x₂,…,x_k); e=1…m. Функцию Y_e, связанную с факторами, называют функцией отклика, а её геометрический образ – поверхностью отклика. Исследователь заранее не известен вид зависимостей Y_l, l=1…m, поэтому используют приближение соотношения: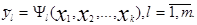

Зависимость и Y_l находятся по данным эксперимента. Последний необходимо поставить так, чтобы при минимальных затратах ресурсов (числе испытаний), варьируя выходные значения по специально сформулированным правилам, построить математическую модель системы и оценить её характеристики. Факторы при проведении эксперимента могут быть управляемыми и неуправляемыми, количественными или качественными, фиксированными и случайными. Фактор относится к изучаемым, если он включён в модель для изучения свойств системы. Количественными факторами являются интенсивности входящих потоков заявок, интенсивности потоков обслуживания, ёмкости накопителей, количество обслуживающих каналов и другие. Качественным факторам не соответствует числовая шкала (дисциплины постановки на очередь, обслуживание каналов и другие).

Фактор является управляемым, если его уровни целенаправленно выбираются экспериментатором.

При планировании эксперимента обычно изменяются несколько факторов.

Основными требованиями, предъявляемыми к факторам - независимость и совместимость. Совместимость означает, что все комбинации факторов осуществимы.

Для выбора конкретной модели планирования эксперимента необходимо сформулировать такие её особенности, как адекватность, содержательность, простота.

План эксперимента обычно используется для определения экстремальной характеристики объекта. Поэтому планирование эксперимента называется экстремальным. В планировании эксперимента наибольшее значение нашли модели в виде алгебраических полиномов.

Предполагаем, что изучается влияние К количественных факторов х_i на некоторую h в отведённый для экспериментирования локальной области факторного пространства ограниченного х_{i min}—x_{i max}, i=1…k.

Функцию отклика обычно выбирают линейной или квадратичной.

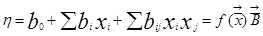(1)

где 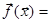вектор с элементами 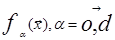, входящих в исходный полином; 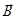- вектор коэффициентов. Для двух факторов имеем: f₀=1, f₁=x₁, f₂=x₂, f₁₂=x₁x₂, f₁₁=x₁², f₂₂=x₂². 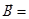(b₀,b₁,b₂,b₁₂,b₁₁,b₂₂).

Так как полином (1) содержит d коэффициентов, то план эксперимента должен содержать N³d различных экспериментальных точек:

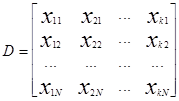
где x_in­ - значение, которое принимает i-ая переменная в u-ом испытании. i=1…k, u=1...N. Матрица D называется планом эксперимента.

Реализовав испытания в N очках области факторного пространства, определённом планом эксперимента, получим вектор наблюдений имеющий следующий вид:

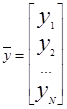
где y_u - реакция соответствующей u-ой точке плана.

Плану эксперимента поставим в соответствие матрицу планирования:

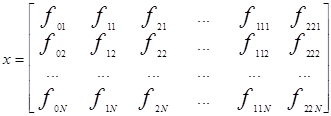
где f_il, f_ijl - координатные функции при соответствующих коэффициентах модели, в l - ом эксперименте.

Построению плана эксперимента предшествует проведение ряда неформализованных действий (принятия решения) направленных на выбор локальной области факторного пространства G.

Необходимо учитывать, что как только модель сформирована включение дополнительных факторов для уточнения модели невозможно. Вначале следует выбрать границы x_{i min} и x_{i max} области определения факторов исходя из свойств объекта. Например, температура при термобарических экспериментах не может быть ниже абсолютного нуля и выше температуры плавления материала из которого изготовлена термобарокамера.

После определения области G необходимо найти нулевые (основные) уровни факторов и интервалы варьирования Dx_i, i=1…k.

Эксперимент, в котором реализуются все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПЭФ). Если выбранная модель включает только линейные члены полинома и их произведения, то для оценки коэффициентов модели используется ПЭ с варьированием всех k факторов на двух уровнях, т.е. q=2. Такие планы называются планы типа 2^k, где n=2^k- число всех возможных испытаний.

Начальным этапом ПЭ для получения коэффициентов линейной модели основан на варьировании факторов на двух уровнях: нижнем x_iн и верхнем x_iв, симметрично расположенных относительно основного уровня x_i0, i=1…k. Геометрическая интерпретация показана ниже на рис. 11.2.:

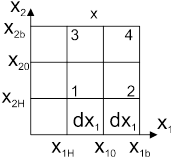
Рис. 11.2. ПЭФ типа 2².

Для упрощения записи условий каждого эксперимента факторы кодируют в виде безразмерных величин 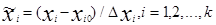.Средний уровень кодированного фактора является нулём 0, граничные значения соответственно +1 и -1.

11.2 Стратегическое планирование машинных экспериментов с моделями систем

Можно выделить стратегическое и тактическое ПЭ на моделях систем.

Стратегическое планирование – ставит своей целью получение необходимой информации о системе S с помощью модели M_M, реализованной на ЭВМ. Оно аналогично внешнему проектированию при создании системы S.

Тактическое планирование – определяет способы проведения каждой серии испытаний машинной модели M_M. Оно аналогично внутреннему проектированию системы S.

Рассмотрим элементы стратегического планирования ПЭ. Его целью может быть:

1. Получение функции реакции системы от независимых фактов: y=f(b₀,b₁…,x₁,x₂,…x_k)

2. Нахождение экстремума: f(b₀,b₁…,x₁,x₂,…x_k).

Во 2-ом случае для определения наилучшей комбинации фактов могут быть использованы методы систематической или случайной выборки.

К систематическим относятся методы:

- одного фактора;

- предельного анализа;

- наискорейшего спуска;

- равномерной сетки.

Проблемой является большое количество факторов. Для k=10 ПЭФ должен состоять из 1024 точек. Используют неполные планы, метод "поверхности реакции".

Следующей проблемой является многокомпонентность функции реакции. Здесь можно использовать последовательное однокомпонентное ПЭ. Этот подход не всегда возможен из-за связанности компонентов. Используются интегральные оценки с применением весовых функций, функций полезности и т.д.

Другой проблемой является стохастическая сходимость результатов ПЭ. В качестве результатов ПЭ используется средние некоторых распределений, для оценки которых применяют выборочные средние, найденные путём многократны прогонов модели на ЭВМ. Сходимость выборочных средних с ростом объема выборки называется стохастической. Эта сходимость, как правило, медленная. Если s - стандартное отклонение среднего N наблюдений будет равно s/ 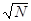, т.е. для уменьшения случайной выборки в k раз требуется увеличить объем выборки в k² раз.

Планирование машинного эксперимента представляет собой итерационный процесс, когда выбранная модель плана эксперимента проверяется на реализуемость, а затем, если это необходимо, вносят соответствующие коррективы в модель.

Планирование эксперимента с моделью проводится в несколько этапов:

1) построение структурной модели;

2) построение функциональной модели.

Структурная модель ПЭ характеризуется числом факторов и числом уровней для каждого фактора. Из опыта известно, что 20% факторов определяют 80% свойств системы.

Ортогональное распределение плана упрощает определение коэффициентов аппроксимации. Упрощение дает принятие числа уровней всех факторов одинаковыми (не больше 3). Функциональная модель ПЭ определяет количество элементов структурной модели N_ф, т.е. необходимое число различных информационных точек N_ф. Причём N_ф<N_с, где N_с=q₁,q₂…q_k – число экспериментов ПФЭ.

11.3 Тактическое планирование машинных экспериментов с моделями систем

Здесь решают проблемы:

- определения начальных условий и их влияния на достижения установившегося результата при моделировании;

- обеспечения точности и достоверности результатов моделирования;

- уменьшения дисперсии оценок характеристик процесса функционирования моделируемых систем;

- выбора правил автоматической остановки имитационного эксперимента с моделями.

Рассмотрим ПФЭ типа 2³:

номер испытания
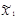
	-1	-1	-1	-1	+1	+1	+1	+1
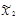
	-1	-1	+1	+1	-1	-1	+1	+1
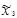
	-1	+1	-1	-1	-1	+1	-1	+1

ПЭФ даёт возможность определить не только коэффициенты регрессии, соответствующие линейным эффектам, но и коэффициенты регрессии соответствующие всем эффектам взаимодействия. Эффект взаимодействия двух или более факторов появляется при одновременном варьировании этих факторов, когда действие каждого из них на выход зависит от уровня, на которых находятся другие факторы.

Для оценки свободного члена b₀ и определения эффектов взаимодействия b₁₂, b₁₃, …,b₁₂₃… план эксперимента D расширяют до матрицы планирования X путём добавления соответствующей фиктивной переменной: единичного столбца 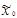и столбцов произведений 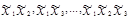как показано, например, для ПЭФ типа 2³ в таблице (см. ниже):

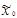
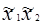
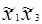
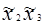
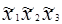
Номер испытания		План ПЭФ					Реакция y
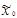
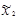
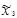
	+1	+1	+1	+1	+	+	+	+	y1
	+1	–1	+1	+1	–	–	+	–	y2
	+1	+1	–1	+1	–	+	–	–	y3
	+1	–1	–1	+1	+	–	–	+	y4
	+1	+1	+1	–1	+	–	–	–	y5
	+1	–1	+1	–1	–	+	–	+	y6
	+1	+1	–1	–1	–	–	+	+	y7
	+1	–1	–1	–1	+	+	+	–	y8

Как видно из рассмотренных ПЭ типа 2² b 2³ количество испытаний ПЭФ значительно превосходит число определяемых коэффициентов линейной модели плана эксперимента, что увеличивает расход ресурсов ЭВМ по времени. Возникает проблема сокращения количества экспериментов.

С этой целью рассмотрим построение планов так называемого дробного факторного эксперимента (ДФЭ). Пусть имеется ПЭФ типа 2². Используя матрицу планирования X, например приведённую в предыдущей таблице, можно вычислить коэффициенты и предусмотреть результаты в виде уравнения:

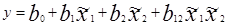
N/n		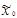План ПЭФ		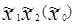Отклик y
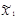
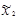
		+1	+1	+1	y1
		–1	+1	–1	y2
		+1	–1	–1	y3
		–1	–1	+1	y4

Если в выбранных интервалах варьирования уровня процесс можно описать линейной моделью, то достаточно определить три коэффициента b₀, b₁,b₂. Т.о. остаётся одна степень свободы, которую можно использовать для построения плана эксперимента D для 3-х переменных, в которых уровни 3-его фактора изменяются как в таблице рассмотренной немного раньше для столбца (эффектов взаимодействия).

Мы получим так называемый дробный факторный эксперимент. В нём уже не будет раздельных оценок для коэффициентов регрессии, как а ПЭФ, они будут рассчитываться по формулам:

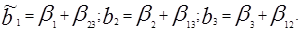
При постулировании линейной модели все парные взаимодействия не учитывают. Т.о. вместо g испытанный в ПЭФ для 3-х факторов получим 4 испытания в ДФЭ. Правило проведения ДФЭ формулируется так: для сокращения числа испытаний новому фактору присваивается значение вектор-столбца матрицы, принадлежащего взаимодействию, которым можно пренебречь.

При проведении эксперимента из 4-х испытаний для оценки влияния 3-х факторов пользуются половинный ПЭФ типа 2³, так называемой "полу репликой". Если приравнять x₃ и x₁x₂, что можно получить 2-ую "полу реплику".

Для обозначения дробных реплик, в которых l линейных эффектов приравнены к эффектам взаимодействия, пользуются условным обозначением 2^k-l. Например, "полу реплика" от 2⁶ записывается в виде 2^6-1, а "четверть реплика" 2^6-2.

Смешивание надо производить так, чтобы основные коэффициенты были смешаны с коэффициентами при взаимодействиях самого высокого порядка. Не рекомендуется использовать реплики для n³15.

Следует иметь в виду, что малый шаг варьирования Dx; (j=1…n) может повлечь статистическую не значимость оценки коэффициента уравнения регрессии. В случае, если полученная мат. модель окажется неадекватной, проводятся эксперименты с меньшим шагом варьирования.

Если линейные модели, построенные с помощью ПЭФ и ДФЭ, неадекватны, то переходят к построению квадратичных моделей.

Оптимальный план для квадратичной модели целесообразно строить таким образом, чтобы он включал точки плана для линейной модели. Это позволяет сократить число опытов.