Структурные элементы СИ

Принцип действия СИ – физический принцип, положенный в основу построения СИ данного типа.

Преобразовательный элемент СИ – элемент СИ, в котором происходит одно из ряда преобразований измеряемой величины.

Измерительная цепь СИ – совокупность преобразовательных элементов СИ, обеспечивающая осуществлением всех преобразований сигнала измерительной информации.

Чувствительный элемент СИ – часть первого в измерительной цепи преобразовательного элемента, находящегося под воздействие измеряемой величины.

Измерительный механизм – часть конструкции СИ, состоящая из элементов, взаимодействия которых вызывают их взаимное перемещение.

Отсчетное устройство – часть конструкции СИ, предназначенное для отсчитывания значений измеряемой величины.

Шкала СИ – часть отсчетного устройства, представляющее собой совокупность отметок.

Отметка шкалы – знак на шкале, соответствующий некоторому значению измеряемый величины. Он может быть в виде черты, точки, зубца.

Числовая отметка шкалы – число, соответствующее некоторому значению измеряемой величины.

Деление шкалы – промежуток между двумя отметками шкалы.

Длина деления шкалы – расстояние между осями двух соседних отметок шкалы, измеренное вдоль воображаемой линии, которая проходит через середину самых коротких отметок шкалы.

Равномерная шкала – шкала с делениями постоянной длины и с постоянной ценой деления.

Неравномерная шкала – шкала с делениями непостоянной длины, а в некоторых случаях и с непостоянной ценой деления.

Указатель – часть отсчетного устройства, положение которой относительно отметок шкалы определяет показание СИ.

Погрешности СИ

Абсолютная погрешность СИ– разность между показательным прибором и действительным значением измеряемой величины. В качестве действительного значения измеряемой величины принимают показания эталонного средства измерения:

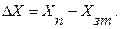(3.1)

где Х п – показание поверяемого средства измерения; Х эт – показание эталонного средства измерения (действительное значение измеряемой величины).

Относительная погрешность СИ определяется как отношение абсолютной погрешности СИ к действительному значению измеряемой величины:

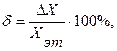(3.2)

где ∆Х – абсолютная погрешность СИ; Х_эт – показание эталонного средства измерения.

Абсолютная погрешность выражается в единицах измеряемой физической величины и может быть задана:

· либо одним числом (линия 1 на рис. 1): Δ = ±а;

· либо в виде линейной зависимости (линии 2 и 3): Δ= ±bх; Δ = ±(а + bх);

· в виде функции Δ=f(х) или графика, таблицы.

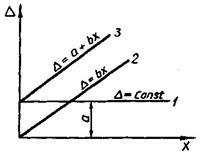
Рисунок 1 – Формирование аддитивной и мультипликативной составляющих погрешности.

Если значение погрешности не изменяется во всем диапазоне измерения (линия 1), например, из-за трения в опорах, то такая погрешность называется аддитивной(или погрешностью нуля).

Если погрешность изменяется пропорционально измеряемой величине (линия 2), то ее называют мультипликативной.

В большинстве случаев аддитивная и мультипликативная со­ставляющие присутствуют одновременно (линия 3).

Приведенная погрешность средств измерений – отношение погрешности измерительного прибора к нормирующему значению:

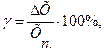(3.3)

где ∆ Х – абсолютная погрешность СИ; Х_норм – некоторое нормирующее значение.

В качестве нормирующего значения могут быть приняты верхний, нижний пределы измерения, диапазон измерения, длина шкалы и т. д.

Также различают статистическую погрешность средств измерений, динамическую погрешность, погрешность средств измерений в динамическом режиме, систематическую погрешность средств измерений, случайную погрешность средств измерений, основную погрешность средств измерений, дополнительную погрешность средств измерений.

Статическая погрешность СИ – погрешность средства измерения, используемого для измерения постоянной величины.

Погрешность СИ в динамическом режиме – погрешность средства измерения, используемая для измерения переменной во времени величины.

Динамическая погрешность СИ – разность между погрешностью средства измерения в динамическом режиме и его статической погрешностью, соответствующей значению величины в данный момент времени.

Систематическая погрешность СИ – составляющая погрешности средства измерения, остающаяся постоянной или закономерно изменяющаяся во времени.

Случайная погрешность СИ – составляющая погрешности средства измерения, изменяющаяся случайным образом.

Основная погрешность – погрешность средства измерения, используемого в нормальных условиях.

Дополнительная погрешность меры - изменение погрешности меры вследствие изменения ее действительного значения, вызванного отклонением одной из влияющих величин от нормального значения или выходом за пределы нормальной области значений.

Предел допускаемой погрешности средства измерения - наибольшая погрешность средства измерения, при которой оно может быть признана годной к применению.

Точность средства измерения - качество СИ, отражающее близость к нулю его систематических погрешностей.

Правильность средства измерения - качество СИ, отражающее близость к нулю его систематических погрешностей.

Сходимость показания средства измерения - качество СИ, отражающее близость к нулю его случайных погрешностей.

Класс точности средства измерения - обобщенная характеристика СИ, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами СИ, влияющими на точность, значение которых устанавливают на отдельные виды СИ.

Классы точности СИ

Классы точности определяются пределами основных и дополнительных погрешностей СИ и устанавливаются в соответствии с ГОСТ 8.401-80 «Классы точности СИ общие требования».

Основной, как отмечалось выше, называется погрешность, соответствующая нормальным условиям применения СИ. Эти условия устанавливаются НТД на виды СИ или отдельные их типы. Ус­тановление условий применения и особенно нормальных условий применения является весьма важным для обеспе­чения единообразия метрологических характеристик средств измерений. В противном случае погрешности СИ одного и того же типа, отнесенные к различным внешним условиям, будут несопоставимы.

Для большинства средств измерений нормальными считаются следующие внешние условия:

· температура окружающей среды (293± 5) К;

· относительная влажность 65% ± 15%;

· атмосферное давление 101,3 кПа ± 4 кПа (750 мм рт. ст. ± 30 мм рт. ст.);

· напряжение питания 220 ± 2% (220 ± 10).

Кроме того, в технической документации на тип СИ указываются рабочие условия, в пределах которых допус­кается применение СИ с гарантированными метрологиче­скими характеристиками.

Представление класса точности пределами основной абсолютной погрешности применяется преимущественно для мер массы и длины. В большинстве случаев классы точности И.П. выражаются пределами допускаемой основ­ной приведенной или относительной погрешности. При этом основой для определения формы представления клас­са точности прибора является характер изменения основ­ной абсолютной погрешности.

Если основная абсолютная погрешность имеет адди­тивный характер, т.е. границы погрешностей измеритель­ного прибора не изменяются в пределах диапазона измере­нии, то класс точности представляется пределами допус­каемой приведенной погрешности:

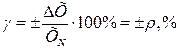(3.4)

где ∆Х – предел допускаемой основной абсолютной погрешности СИ; ρ – отвлеченное положительное число, выбираемое из следующего ряда чисел:

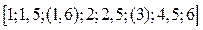^.10ⁿ

Х_N – некоторое нормирующее значение (диапазон измерений, верхний или нижний предел измерений или длина шкалы).

Если основная абсолютная погрешность имеет мультипликативный характер, т.е. границы погрешностей измеренного прибора линейно меняются в пределах диапазона измерений (рис. 2), то класс точности представляется пределами допускаемой относительной погрешности δ в виде:

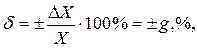(3.5)

где 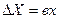– пределы допускаемой основной абсолютной погрешности прибора (в = tgλ);

Х – показание прибора; g – отвлеченное положительное число.

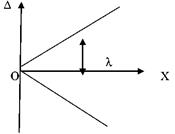
Рисунок 2- Зависимость погрешности от значений шкалы

Если основная абсолютная погрешность СИ имеет аддитивные и мультипликативные составляющие, то класс точности представляется пределами допускаемой относительной погрешности δ в виде:

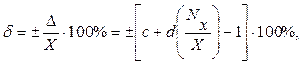(3.6)

где 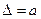+ вх; с и d – отвлеченные положительные числа.