Метод узловых потенциалов. Составление уравнений для разветвлённой цепи, содержащей источники ЭДС и источники тока.

Можно так же уменьшить число уравнений для расчёта токов в электрической цепи, если составлять только узловые уравнения для токов. Выполнение второго закона Кирхгофа обеспечивается соответствующим выражением всех токов по закону Ома через разность потенциалов:

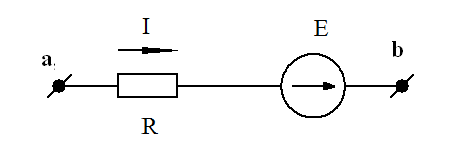
Рис. 26 Схема ветви

ϕ_a – ϕ_b = IR – E (95)

I= 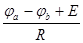= (φ_a – φ_b + E)g; g = 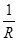(96)

Выражая из уравнения (95) ток, можно быть уверенным в том, что второй закон Кирхгофа выполняется автоматически.

Рассмотрим метод узловых потенциалов на примере схемы рис. 27

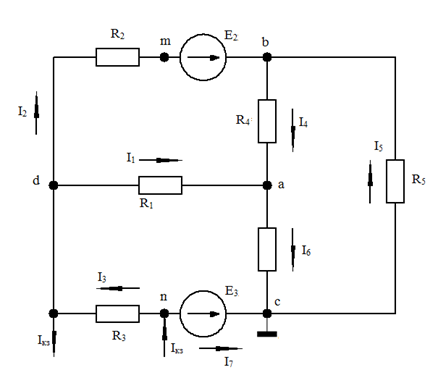
Рис. 27. Схема электрической цепи

Токораспределение в схеме не изменится, если один из узлов схемы заземлить, т.е. принять потенциал этого узла равным нулю.

Пусть φ_с = 0, а значит φ_n = -Е₃. Теперь известны потенциалы двух узлов, поэтому достаточно составить три уравнения для узлов а, b, d.

Число уравнений, которые нужно составить по методу узловых потенциалов всегда равно числу узлов, потенциалы которых неизвестны.

Система уравнений в наиболее общем случае, т.е. когда в схеме имеются и источники ЭДС и источники тока, имеет следующий вид для схемы рис. 27:

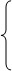φ_ag_aa – φ_bg_ab – φ_dg_ad = 0;

–φ_ag_ba + φ_bg_bb – φ_dg_bd = E₂g_bd; (97)

–φ_ag_da – φ_bg_db + φ_dg_dd = -E₂g_bd – E₃g_dс – I_кз;

Здесь g_aa, g_bb, g_dd – суммарная проводимость всех ветвей, сходящихся соответственно в узлах a, b, d.

g_ab, g_ad, g_bd, g_dc - проводимости ветвей между соответствующими узлами.

Очевидно, что g_ab = g_ba, g_ad = g_da, g_bd = g_db, g_dc = g_cd.

В левой части уравнений (97) члены, содержащие суммарные проводимости, берутся со знаком «плюс», а все остальные члены – со знаком «минус».

В правой части уравнения (97) стоят алгебраические суммы произведений ЭДС на проводимости соответствующих ветвей, сходящихся в узлах, а так же алгебраическая сумма токов от источников токов, подходящих к узлам. Произведение ЭДС Е на проводимость g берётся со знаком «плюс», если ЭДС Е направлена к узлу схемы, и со знаком «минус», если ЭДС Е направленна от узла схемы.

Первое уравнение в системе (97) составлено для узла а, второе – для узла b, третье – для узла d.

Для схемы рис. 27 имеем:

g_aa = 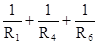; (98)

g_bb = 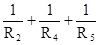; (99)

g_dd = 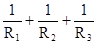; (100)

g_ab = g_ba = 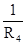; g_ad = g_da = ;

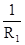g_bd = g_db = 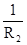; g_dc = g_cd = 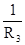. (101)

Ток от источника тока, протекающий к узлу, берётся со знаком «плюс», а оттекающий от узла – со знаком «минус».

Подставив заданные значения сопротивлений резисторов, ЭДС и источника тока получим систему из трех уравнений, неизвестными в которой являются потенциалы φ_a, φ_b, φ_d.

Воспользуемся для решения, например, методом Крамера:

φ_a = 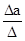; φ_b = 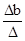; φ_d = 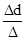; (102)

где 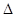- главный определитель.

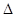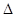_a, _b, 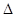_d – частные определители.

Далее найдем токи в ветвях по закону Ома:

I₁= 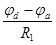; (103)

I₂= 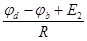; (104)

I₃= 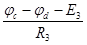= 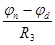; (105)

I₄= 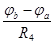; (106)

I₅= 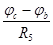; (107)

I₆= 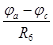; (108)

I₇= I_кз + I₃; (109)