Математична економіка та економетрія.

Математична економіка - розділ економічної науки, що займається аналізом властивостей та розв'язків математичних моделей економічних процесів. В математичній економіці досліджуються теоретичні моделі, що будуються на деяких формальних передумовах. Задачею математичної економіки є вивчення питання про існування розв'язку моделі, умови його невід'ємності, стаціонарності та інших властивостей. Це робиться, як звичайно в математиці, шляхом дедуктивного одержання висновків із апріорно зроблених передумов (аксіом).

Економетрія займається статистичною оцінкою та аналізом економічних залежностей та моделей на основі вивчення емпіричних даних. Основою економетрії являється кореляційно-регресійний аналіз.

Традиційним уявленням про математичну модель є її сприйняття як інструменту для прогнозування наслідків альтернативних дій з метою вибору найкращого. Проте значно важливий те, що моделювання – це метод, що підвищує ефективність думок і рішень.

Математичні моделі використовуються для формалізації цілей, властивих більшості економічних систем, і наявних обмежень, що накладаються діючими економічними законами.

Проте є велика кількість проблем, непіддатливих адекватному моделюванню, наприклад:

захист навколишнього середовища від забруднень,

запобігання злочинності,

управління розвитком і зростанням міст, і т.п.,

Вони характеризуються неясністю і суперечністю цілей, альтернатив розвитку, диктованих нестабільними політичними і соціальними чинниками.

Математичні моделі багатофункціональні, їх основні функції характеризують широту області їх застосування:

1. Моделі є важливим засобом осмислення дійсності (графічні, масштабні, мережеві моделі).

2. Моделі виступають своєрідним засобом спілкування, оскільки в стислій, точній формі дозволяють організувати діалог.

3. Моделі виконують функцію навчання і тренажу (повчальні програми, імітаційні ігри на ЕОМ, що використовують принципово відмінні від реальних стимули і мотиви ухвалення рішень).

4. Моделі широко використовуються як інструмент прогнозування і планування, дозволяючи розглянути значне число альтернатив і оцінити можливі наслідки від ухвалення того або іншого рішення.

5. Моделювання є основним методом оптимізації управлінських рішень, відображаючи або відтворюючи умови розвитку досліджуваного процесу.

6. Застосування моделей як засоби побудови експериментів дозволяє здійснювати управління процесом експериментування з більшою простотою і меншими витратами, ніж якби експеримент проводився з реальною системою, одержуючи, часто, більше корисної інформації про поведінку системи в умовах широкого спектру чинників зовнішнього середовища, що змінюються.

Економіко-математичної моделі: це сукупність математичних виразів, що описують економічні об'єкти, процеси і явища, дослідження яких дозволяє одержати необхідну інформацію для реалізації цілей управління модельованою системою.

Економіко-математична модель, як правило, включає три основні складові частини:

1. цільову функцію, або функціонал моделі – математичний вираз мети;

2. систему функціональних обмежень, що визначають межі зміни досліджуваних характеристик об'єктів, процесів або явищ;

3. систему параметрів моделі, фіксуючих умови проведення модельного експерименту (система норм, нормативів, тимчасові параметри реального часу, системного часу, початкові умови і т.п.).

У загальному вигляді статична економіко-математична модель системи може бути записана у вигляді:

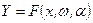, (2.7)

де 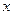– екзогенні змінні, або управління, керовані змінні; чинники; входи;

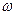– некеровані змінні, або обурення;

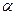– параметри системи; будь-які дійсні числа;

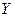– ендогенні, або залежні змінні, відгуки;

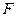– визначає вид функціональної залежності, грає роль оператора перетворення.

Класифікація моделей.

При класифікації економіко-математичних моделей враховуються різні ознаки, кожен служить певній меті. Деякі типові групи моделей, які можуть бути встановлені в основу системи класифікації:

-статичні і динамічні;

-детерміновані і стохастичні;

-дискретні і безперервні;

-лінійні і нелінійні;

-балансові моделі;

-імітаційні моделі;

-моделі математичного програмування;

-моделі, засновані на теорії графів;

-моделі, засновані на теорії вірогідності і математичній статистиці.

При моделюванні складної системи дослідник звичайно досліджує сукупність декількох моделей з числа різновидів, згаданих вище. Будь-яка система може бути представлена різними способами, відмінними по складності і в деталях. У міру того, як дослідник глибше аналізує і пізнає проблему, прості моделі зміняються все більш складними.