Треугольником и звездой.

Если при смешанном соединении резистивных элементов не удается определить эквивалентное резистивное сопротивление, то необходимо эквивалентное преобразование таких цепей. Примером упрощения расчетов служит преобразования мостовой схемы соединения резистивных элементов (рис. 1.16).

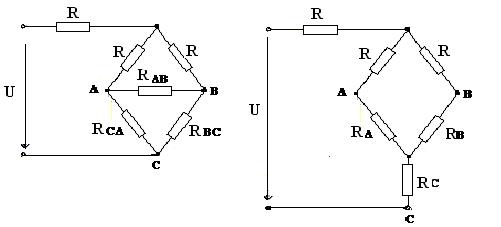
Рис.1.16. Преобразование мостовой схемы в эквивалентные схемы, соединённые звездой и треугольником

После замены треугольника ABC с резисторами 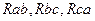эквивалентной звездой ABC с резисторами , всю цепь можно рассматривать как смешанное соединение резисторов.

Для преобразования треугольника в эквивалентную звезду, найдем сопротивление между узлами A и B.

Для схемы треугольника проводимость между узлами A и B определим из соотношения:

.

Тогда сопротивление между узлами A и B будет:

( )/ .

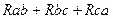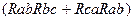Для схемы звезды сопротивление между узлами A и B равно: .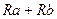

Согласно условию эквивалентности можно записать равенство:

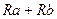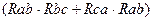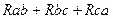= /( ). (1.37)

Аналогично, путем циклической перестановки индексов, можно получить уравнения равенства сопротивлений между узлами B и C, C и A:

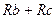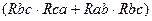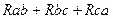= /( ), (1.38)

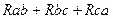= /( ). (1.39)

Для определения сопротивления звезды сложим (1.41) и (1.43), вычтем (1.42) и, разделив полученное выражение на 2, найдем

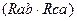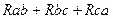= /( ). (1.40)

Путем циклической перестановки найдем сопротивления 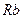и :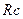

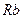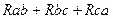= /( ) (1.41)

Rc = 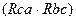/( 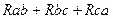). (1.42)

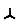В случае равенства сопротивлений ветвей треугольника, сопротивления ветвей эквивалентной звезды тоже одинаковы и определяются по формуле:

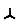R = R∆ / 3. (1.43)

При обратном преобразовании звезды в эквивалентный треугольник перемножим попарно (1.44) и (1.45), (1.45) и (1.46), (1.46) и (1.44) и сложим полученные произведения:

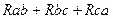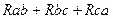= ( ) / ( ). (1.44)

Выражение (1.48) разделим на (1.46) и определим сопротивление 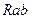ветви треугольника:

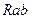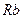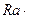
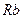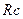= + +( ) / . (1.45)

Путем циклической перестановки найдем сопротивления 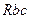и 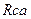других ветвей треугольника:

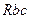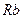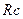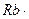
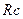= + + ( ) / ; (1.46)

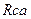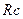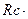
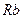= + +( ) / . (1.47)

При равенстве сопротивлений ветвей звезды, сопротивления ветвей эквивалентного треугoльника тоже одинаковы и определяются по формуле:

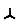R∆ =3R . (1.48)