МЕТОД П. О. ПАШКОВА.

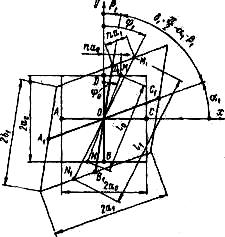
Исходная квадратная ячейка дели­тельной сетки, нанесенной в главной плоскости, превращается В параллелограмм (рис. 8.2). Система координат хОу принимается с началом в точке О — центре ячейки.

Параметрами, отображающими искажение ячейки, как и раньше, будут стороны параллелограмма 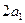и и 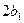угол между ними δ₁, а поворот относительно фиксированных на плоскости осей координат характеризуют углы 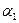и 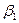, причем:

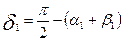. (8.5)

Длина 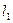и направление (угол 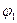) некоторого отрезка 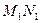,имеющего до деформации длину 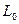и направление, определяемое параметром п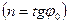, значение которого по условию однородности деформаций постоянно, используются для определения деформации удлинения этого отрезка:

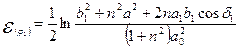. (8.6)

Соответственно определяется:

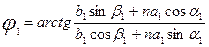. (8.7)

Рис. 8.2. Искажение квадратной ячейки делительной сетки

По П. О. Пашкову.

Значения параметра п, определяющие направления главных осей деформации, находятся из условия их экстремума:

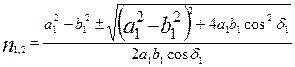(8.8)

Перед радикалом знак (+) соответствует 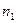, а минус — .

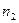Подставляя значения 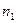и 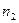в уравнение (8.6), получим:

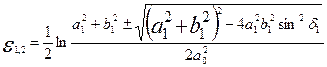(8.9)

т. е. тот же результат, что и по методу Э. Зибеля — см. уравнение (8.3). Интенсивность деформированного состояния определяется по уравнению (8.4).

Расчетные формулы методов Э. Зибеля и П. О. Пашкова таковы,
что исходная ячейка делительной сетки должна обязательно
иметь квадратную форму. Погрешность в нанесении ортогональной
сетки может, очевидно, привести к ошибке в определении, как значений главных компонентов деформаций, так и направлений главных осей.

Лекция № 9.