Послідовність виконання структурного аналізу.

1. Будують структурну схему механізму. Дають характеристику ланок і кінематичних пар.

2. Визначають ступінь вільності механізму.

3. Вилучають пасивні умови зв’язку та зайві ступені вільності.

4. Якщо механізм має вищі кінематичні пари ІV класу, їх замінюють на нижчі пари V класу.

5. Розкладають механізм на структурні групи Ассура та механізм (механізми) І класу. Кількість механізмів І класу має дорівнювати числу ступенів вільності механізму.

6. Визначають клас і порядок виділених груп Ассура.

7. За класом старшої групи Ассура визначають клас (і порядок) механізму в цілому.

8. Записують структурну формулу механізму (формулу будови).

При розкладі механізму на групи Ассура (п.5) слід пам’ятати, що в групу Ассура входять лише рухомі ланки; число ланок в групі завжди парне, а число кінематичних пар кратне трьом; розпочинати виділення групи треба з ланок найвіддаленіших від початкової ланки. Оскільки в практиці найбільше груп Ассура ІІ класу, то спочатку намагаються відокремити кінематичний ланцюг, що містить дві ланки та три кінематичні пари. Ступінь рухомості механізму, що залишається, має бути таким, як і в п.2, а виділеного кінематичного ланцюга – звичайно нуль. Якщо виділити двоповодкову групу не вдається, то роблять спробу виділити ланцюг із 4 ланок і 6 кінематичних пар. Після відокремлення однієї групи Ассура виділяють наступну і так доти, доки не залишиться механізм І класу.

Приклад структурного аналізу. На рис. 1.11 наведена структурна схема шестиланкового механізму поршневої помпи: 1 – кривошип; 2, 4 – шатуни; 3 – коромисло; 5 – повзун; 6 – стояк. Число рухомих ланок дорівнює п’яти, n = 5.

Число кінематичних пар: р₅= 7, це пари: А(1, 6); В(1, 2); С(2, 3); Д(3, 6); Е(3, 4); F(4, 5) – обертові пари та F^/(5, 6) – поступальна пара; р₄= 0, тобто вищих кінематичних пар немає.

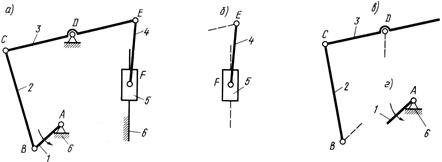
Рис. 1.11

Ступінь вільності механізму за формулою Чебишева

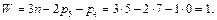
Даний механізм має один ступінь вільності і, відповідно, має бути один механізм І класу, - одна початкова ланка.

Розкладаємо механізм на групи Ассура. Послідовно від’єднуємо від механізму дві групи Ассура ІІ класу ІІ порядку, одна з них ІІ виду (ланки 4, 5), друга І виду (ланки 3, 2). В результаті залишається механізм І класу (ланки 1, 6).

Враховуючи, що групи 2, 3 та 4, 5 є групами ІІ класу, можна зробити висновок, що даний шестиланковий механізм належить до другого класу.

Інколи склад та послідовність приєднання груп Ассура в механізмі виражають структурною формулою

І(1, 6) 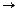ІІ(2, 3) 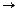ІІ(4, 5)

З цієї формули видно, що до механізму І класу, який утворений ланками 1 та 6, послідовно приєднали групу Ассура ІІ класу, утворену ланками 2, 3, і групу Ассура ІІ класу – ланки 3, 4.

Умовна заміна в плоских механізмах вищих пар нижчими. Замінюючі механізми. Під час класифікації, вивчення структури та кінематики плоских механізмів з вищими парами в багатьох випадках зручно умовно замінювати вищі пари нижчими. При цьому, треба задовільнити умови структурної та кінематичної еквівалентності замінюючого і реального механізмів: замінюючий механізм повинен мати такий самий ступінь вільності і необхідно, щоб характер миттєвого відносного руху всіх його ланок не змінився.

У плоских механізмах вища кінематична пара утворюється шляхом дотику двох кривих, по яких окреслені її елементи (рис. 1.12). Інколи одним з елементів пари може бути точка або пряма. Для кожної з кривих можна знайти у точці їх дотику радіус та центр кривини. Обидва центри та точка дотику розміщені на спільній прямій – нормалі до кривих. У ТММ доведено, що вища кінематична пара IV класу еквівалентна до ланки та двох нижчих пар V класу. Положення додаткової ланки співпадає з спільною нормаллю до кривих у точці їх дотику, а довжина дорівнює сумі радіусів кривини елементів вищої пари. Нижчі кінематичні пари розміщують у центрах кривини профілів, що дотикаються, тобто на кінцях додаткової ланки.

Розглянемо приклад. Нехай заданий механізм з вищою парою, елементи ланок якої являють собою довільні криві a та b (рис. 1.12, а). Для заміни вищої пари нижчими та побудови схеми замінюючого механізму проведемо нормаль nn в точці С дотику кривих а та b і відмітимо на ній центри О₁, О₂ кривини. В точках О₁, О₂ розміщуємо обертові кінематичні пари V класу і з’єднуємо їх з центрами А і В. Отже, вища пара ІV класу в точці С замінюється умовною ланкою О₁O₂та двома кінематичними парами V класу О₁і О₂ Даний механізм буде еквівалентний плоскому шарнірному чотириланковику АО₁O₂В - замінюючий механізм. Зазначимо, що якщо профілями вищої пари є криві змінної кривини, у кожному положенні розміри замінюючого механізму змінюються.

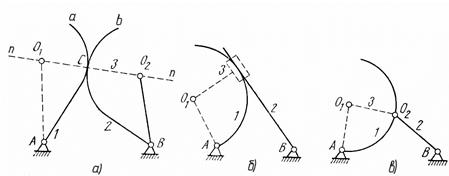
Рис. 1.12

На рис. 1.12, б, в наведено інші приклади заміни вищих кінематичних пар нижчими. Якщо одна з ланок, що утворює вищу пару, буде мати прямолінійний профіль, то замість обертової пари вводиться поступальна (центр кривини такого профілю знаходиться на нескінченості). У випадку, коли одним з елементів є точка (загострення), то радіус кривини звичайно дорівнює нулю, і, відповідно, одна з обертових пар буде знаходитися у даній точці.

Питання для самоконтролю

1. Що вивчає ТММ?

2. Дайте визначення механізму, машини.

3. Назвіть дві основні проблеми ТММ.

4. Що називається ланкою, кінематичною парою?

5. За якими ознаками класифікують кінематичні пари?

6. Що називається кінематичним ланцюгом? Як їх класифікують?

7. Яка різниця між механізмом та кінематичним ланцюгом?

8. Запишіть формулу Чебишева.

9. За якою формулою визначають ступінь вільності просторового механізму?

10. Наведіть приклади основних механізмів з нижчими парами та їх структурні формули.

11. Наведіть приклади основних механізмів з вищими парами