Арифметичні суматори

Це функціональні вузли, що здійснюють арифметичне додавання чисел. У цифровій техніці підсумовування виконується в ос­новному над двійковими (рідше двійково-десятковими) числами. Додавання багаторозрядного слова за допомогою суматора здійснюється порозрядно з урахуванням переносу в сусідній старший рпзряд. Тому при побудові суматора необхідно враховувати не лише появу переносу в да­ному розряді, але й можливість одержання аналогічного переносу від сусіднього молодшого розряду.

За принципом побудови і типом використаних елементів розрізняють комбінаційні та накопичуючі суматори. Результати проміжного порозрядного додавання у накопичуючих суматорах зберігаються в елементарних комірках пам'яті, функцію яких викоиують тригери. Комбінаційні суматори не мають запам’ятовувачів. У них додавання двійкових чисел здійонюється позиційним кодои одночасно, як і у звичайних КП, результат на виході у комбінаційних суматорах зникає зразу після припинення дії вхідних сигналів. Тому до складу комбіна­ційних суматорів, як правило, входять вхідні та вихідні регістри, тоб­то пристрої, що здатні записувати чи перезаписувати проміжний резуль­тат підсумовування у послідовному або у паралельному коді.

Для додавання двійкових чисел можуть застосовуватись як одно-, так і багаторозрядні суматори, а сама процедура підсумовування може здійсню­ватись або послідовно, починаючи з молодпого розряду, або паралельно, коли всі розряди чисел додаються одночасно. Важливою ознакою паралель­ного суматора є спосіб організації переносу при підсумовуванні. Роз­різняють суматори з послідовним, паралельним (наскрізним) та групо­вим переносом.

Як послідовні, так і паралельні суматори будуються на основі комбінаційного однорозрядного суматора, що складається з напівсуматора.

Напівсуматор - це пристрій (рис. 3.11), що має два входи (для доданків a і b) і два виходи (суми S і переносу P), і призначений для виконання арифметичних дій за правилами, що наведені у табл. 3.3. З таблиці істинності (табл. 4.5) видно, що напівсуматор виконує елементарне додавання двох однорозрядних двійкових чисел та сумовування отриманого результату з переносом у наступний старший розряд. Тому логічна структура напівсуматора має відображати стан обох виходів згідно з виразами:

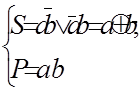( 3.0 )

Відповідно до наведених виразів логічна структура напівсуматора має містити два ЛЕ: суматор за модулем 2 і кон'юнктор, шо зображені на рис. 3.11.б.

Таблиця 3.12 Виконання арифметичних дій за правилами напівсуматора

Однак у логіці роботи напівсуматора не передбачено переносу з сусіднього молодшого розряду, тому напівпуматор може здійснювати додавання тільки у молодшому розряді двійкових чисел. Поява одиниці переносу при додаванні двох розрядів (числа і переносу) дещо змінює правила підсумовування двійкових чисел. Такий однорозрядний суматор потребує ще один (третій) вхід переносу з сусіднього молодшого розряду. Для цього служить так званий повний суматор.

Повний суматор (рис. 3.12) реалізує процедуру додавання двох однорозрядних двійкових чисел з урахуванням переносу з молодшого розряду. Тому він має три входи (a_i, b_i, P_i) і два виходи (S_i і P_i+1). Логіка роботи повного суматора наведена у табл. 4.6, де a_i, b_i -доданки двійкових чисел в i-му розряді; P_i, P_i+1- переноси, відповідно з молодшого розряду i в сусідній старший розряд i+1; S -утворена сума в i-му розряді.

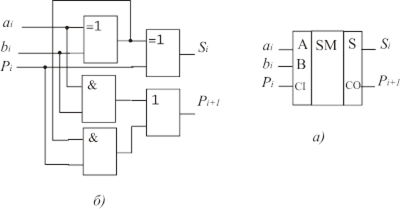
Рис. 3.38 Повний суматор

Таблиця 3.13 Виконання арифметичних дій для повного суматора

Згідно з таблицею істинності (табл. 3.4) робота повного суматора двійкових чисел описується такими логічними виразами:

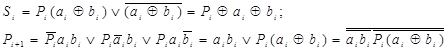( 3.0 )

За виразами (3.8) тепер можна побудувати повний суматор, структурна схема та умовне позначення якого зображені на рис. 3.12 (СІ -вхід переносу, від англ. Carry Input, а СO-вихід переносу, від англ. Carry Output).

Для додавання двох n-розрядних двійкових чисел A і B потрібно, очевидно, використати n однорозрядних повних суматорів. При цьому можуть бути два способи підсумовування - послідовне і паралельне. Застосування того чи іншого принципу підсумовування залежить від характеру вводу/виводу чисел та організації переносів багаторозрядного суматора.