Шифратори та дешифратори
Шифратор призначений для перетворення цифрової інформації, що подана унітарним n-розрядним кодом, у еквівалентний двійковий m‑розрядний код.
Унітарний код це код для якого може існувати тільки один активний стан змінної Xi із множини вхідних сигналів {Xn-1…X1,X0}. Отже, шифратор - це перетворювач унітарного коду "1 з n" у двійковий паралельний код, у якого число виходів m однозначно зв’язане з числом входів n як 2m. Якщо n=2m , що означає використання повного набору вихідних двійкових комбінацій Yi, такий шифратор називають повним. Наприклад, шифратор 8-3 є повним, бо він реалізує повний набір можливих комбінацій змінних Xi (n=8) у повний вихідний набір Yi (m=2) як 23=8.
У неповному шифраторі число входів m не відповідає числу всіх можливих вихідних комбінацій 2m, причому завжди n<2m, що відповідно утворює певне число невикористаних вихідних наборів. Прикладом неповного шифраторa, який найчастіше зустрічається на практиці, є шифратор 10-4, що використовується для кодування десяткових чисел у двійково-десятковий код ДДК /8-4-2-1/, Такий шифратор можна застосовувати для кодування десяткових символів (0...9), наприклад, з клавіатури пульта керування. Схематичне позначення шифратора наведене на рис.3.1а, а схема внутрішньої будови на рис.3.1б. Здійснити синтез повного або неповного шифратора можна на базі ЛЕ. Як приклад, здійснимо синтез повного шифратора 8-1.
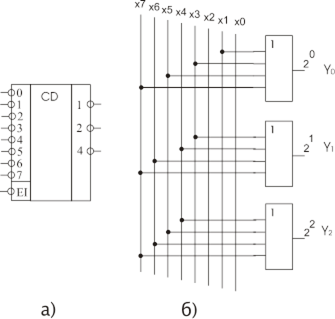
Рис. 3.27 Умовне позначення та внутрішня будова шифратора 8-3
Такий шифратор може бути описаний наступною системою логічних функцій:
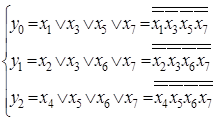 ( 3.0)
( 3.0)
або таблицею істинності:
Таблиця 3.10 Таблиця істинності шифратора 8-3
| n | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | Y2 | Y1 | Y0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Окремі ІС практично зустрічаються рідко, як правило існують мікросхеми, що виконують комбіновані функції, наприклад "шифратор/дешифратор". Крім того, практично використовують шифратори, у яких вихідний код завжди має найбільший номер активного вхідного сигналу {X0..Xn} – так звані пріорітетні шифратори. Приклад роботи пріорітетного шифратора: Вхід{x0=1,x1=1,x2=0, x3=0, ,x4=1}, тоді вихід Y=4.
Дешифратор призначений для розпізнавання (дешифрацій) числа, яке подане позиційним 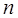 -розрядним двійковим кодом. Найчастіше дешифратор
-розрядним двійковим кодом. Найчастіше дешифратор 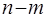 виконує функцію перетворення двійкового кода в унітарний код "1 з
виконує функцію перетворення двійкового кода в унітарний код "1 з 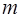 ", тобто виконує функцію, що обернена дії шифратора, і тому для повного дешифратора справедливе співвідношення
", тобто виконує функцію, що обернена дії шифратора, і тому для повного дешифратора справедливе співвідношення 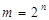 де
де 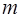 - порядковий номер виходу
- порядковий номер виходу 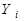 дешифратора. Аналітичний опис дешифратора розглянемо на прикладі повного дешифратора 3-8, який описується системою логічних функцій:
дешифратора. Аналітичний опис дешифратора розглянемо на прикладі повного дешифратора 3-8, який описується системою логічних функцій:
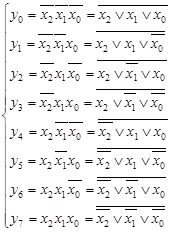 ( 3.0 )
( 3.0 )
Такому опису відповідає схематичне представлення дешифратора на рис. 3.2 а, та його внутрішня будова (рис.3.2.б).

Рис. 3.28 Схематичне позначення та внутрішня структура дешифратора 3-8
У неповного дешифратора число виходів 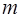 не відповідає значенню
не відповідає значенню 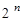 , причому
, причому 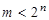 . В інтегральному виконанні зустрічаються як повні (К155ИД3, К155ИД7), так і неповні (К555ИД5, К555ИД10, К561ИД1), а також здвоєні (К155ИД4) дешифратори.
. В інтегральному виконанні зустрічаються як повні (К155ИД3, К155ИД7), так і неповні (К555ИД5, К555ИД10, К561ИД1), а також здвоєні (К155ИД4) дешифратори.
У випадках, коли потрібно побудувати дешифратор на велику кількість виходів на базі дешифраторів з меншим числом виходів, застосовують принцип каскадування. Він полягає у тому, що дані входи дешифраторів розбивають довільним чином на групи, кожна з яких реалізує свою групу логічних функцій. При цьому всі дешифратори повинні бути керованими, тобто мати дозволяючі входи EІ. На рис. 3.3 показано двокаскадне з’єднання двох дешифраторів 3-8 для побудови повного дешифратора 4-16, що має входи дозволу 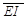 . Каскад 1 працює при активних входах
. Каскад 1 працює при активних входах 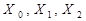 за умови
за умови 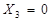 . Як тільки на входах дешифратора з'явиться код {
. Як тільки на входах дешифратора з'явиться код { 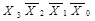 }={1000}, верхній каскад закриється, оскільки
}={1000}, верхній каскад закриється, оскільки 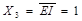 , а відкриється нижній каскад, який через інвертор отримує дозволяючий рівень
, а відкриється нижній каскад, який через інвертор отримує дозволяючий рівень 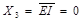 .
.
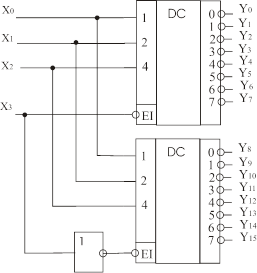
Рис. 3.29 Каскадний синтез дешифратора 4-16
Дата добавления: 2016-07-22; просмотров: 10125;











