Дешифратори-демультиплексори

Демультиплексори – це цифрові комбінаційні пристрої, функціональне призначення яких протилежне функціональному призначенню мультиплексорів. У них сигнали з одного інформаційного входу х розподіляються на 2^m виходів y_i , які комутуються m адресними входами, тобто фактично вони є генераторами мінтермів. Завдяки цій властивості легко створювати канонічні суми, тобто реалізовувати за допомогою логічних операцій АБО логічні функції вхідних змінних.

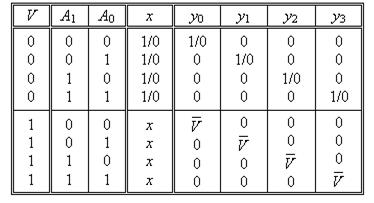
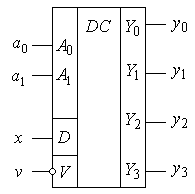
Якщо прийняти кількість адресних входів m = 2 (рис. 2.16), то роботу пристрою описуватимуть булеві рівняння (2.11). Прикладом табличної форми запису роботи демультиплексора, згідно з рівняннями (2.11), є табл. 2.7.

Таблиця 2.7.

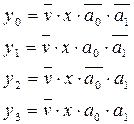
(2.11)

У відповідності до схеми рис. 2.16, активними станами виходів 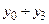є логічні “1”.

У мікросхемах ТТЛ виходи часто мають інверсні значення, і активні стани характеризуються низьким рівнем сигналу.

Рис.2.16.	Рис.2.17.

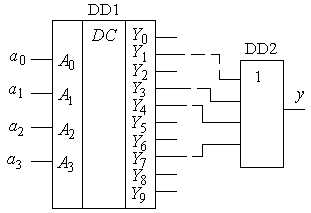
Особливістю більшості серійних мікросхем є їх багатофункціональність. Приведена на рис. 2.17 мікросхема DD1 дешифратора при 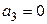виконуватиме функцію перетворювача трьохрозрядного двійкового коду у вісімковий. Значення 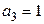при цьому буде заборонено. Якщо на вхід 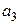подавати послідовний двійковий код, а входи 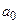, , 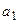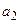використовувати як адресні, то одержимо демультиплексор “з 1 на 8”.

Приклад 2.14. Розробити цифровий комбінаційний автомат, що виконує перетворення чотирьохрозрядного двійкового коду в код “2 з 5” та коду “2 з 5” в двійковий код.

Розв’язання. Код “2 з 5” використовується для безпомилкової передачі цифрової інформації. В цьому п’ятирозрядному коді кожна допустима комбінація містить дві одиниці та три нулі і, оскільки таких комбінацій десять, то кожна з них відповідає одній десятковій цифрі (табл. 2.8).

Таблиця 2.8.

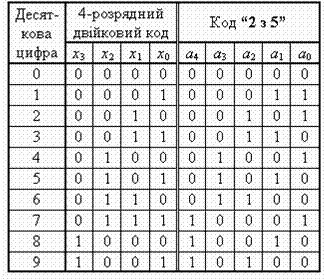
Мінімізуючи функції 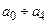, отримаємо вирази для вихідних сигналів:

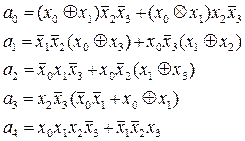
які легко реалізовуються у базисі комбінаційної логіки або з допомогою дешифратора.

Приклад 2.15. Використовуючи дешифратор, призначений для перетворення чотирьохрозрядного двійкового коду в напругу низького логічного рівня, що з’являється на одному з шістнадцяти виходів 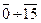, реалізувати логічну функцію:

.

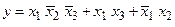Для реалізації функції використовувати багатовходові логічні елементи з множини І, І-НІ, АБО, АБО-НІ.

Розв’язання. Для реалізації функції приведемо її до досконалої диз’юнктивної нормальної форми:

.

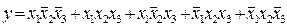Понизивши порядок індексів при логічних змінних, отримуємо:

.

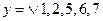Використовуючи шестивходовий елемент К1533ЛА2 І-НІ(зарубіжні аналоги – 7430PC, CDB430E, MH7430, SN7430N, UCY7430N), отримаємо схему, яка реалізовуватиме задану функцію (рис. 2.18).

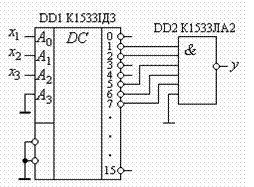Рис.2.18.

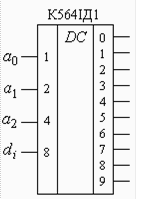Рис.2.19.

Приклад 2.16. Використовуючи дешифратор К564ИД1, розробити пристрій для перетворення двійкового однобайтного коду, заданого в послідовному форматі, в код, представлений у паралельному форматі.

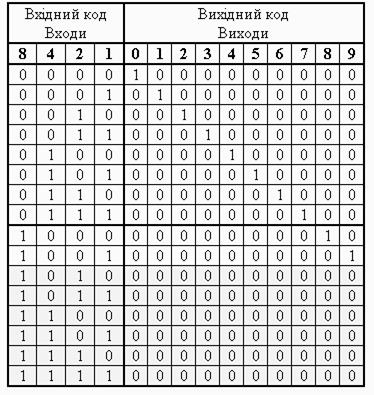
Розв’язання. Дешифратор К564ИД1 – це перетворювач чотирьохрозрядного двійкового коду в прямий десятковий. Він має чотири входи розрядів двійкового коду (1, 2, 4, 8) і 10 виходів розрядів десяткового коду (0 9) (рис. 2.19). Табл. 2.9 є таблицею істинності мікросхеми і пояснює її роботу.

Для використання дешифратора К564ИД1 у якості демультиплексора входи 1, 2, 4 необхідно використовувати як адресні а₀, а₁, а₂, а вхід 8 як вхід даних послідовного формату. На вихідних шинах 0 7 отримуватимемо рознесені в часі значення двійкового коду, який подається на вхід 8в інвертованому виді.

На рис. 2.20 зображені часові діаграми роботи пристрою при подачі на вхід 8 послідовного двійкового коду d_і .

Таблиця 2.9.

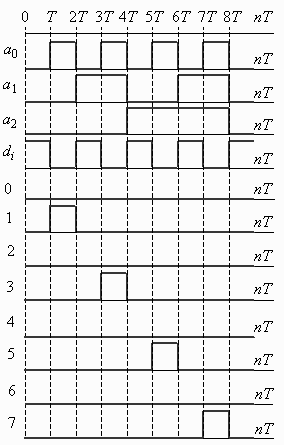Рис.2.20.

Дешифратори широко використовуються для реалізації логічних функцій. Наприклад, для реалізації функції:

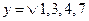
достатньо об’єднати виходи 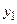, , 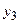, 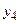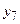за допомогою чотирьохвходового елемента АБО (DD2 на рис. 2.17).

Якщо виходи 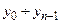дешифратора інвертовані, то об’єднання виходів відповідних диз’юнкцій забезпечується елементами, що реалізують операцію І-НІ.

Використання дешифраторів як генераторів мінтермів корисно в тих випадках, коли необхідно реалізовувати систему логічних функцій. При використанні дешифраторів для реалізації логічних функцій відпадає необхідність їх мінімізації. Більш того, їх необхідно приводити до досконалої диз’юнктивної форми.

Приклад 2.17. Комбінаційна схема визначена за допомогою наступних рівнянь:

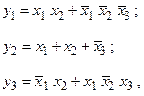
Розробити схему, що реалізує ці три рівняння за допомогою дешифратора та зовнішніх логічних елементів.

Розв’язання. Для вирішення цієї задачі перетворимо функцію до вигляду:

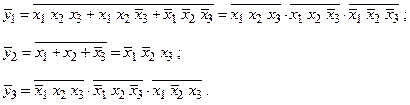
Із приведених функцій бачимо:

1) функція у₂ може бути отримана за допомогою звичайного інвертора, підключеного до виходу, відповідного ;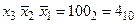

2) функція у₁ отримується об’єднанням через елемент 3І-НІ виходів, відповідних ; ; ;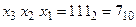

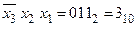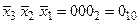3) аналогічно, функція у₃ отримується шляхом об’єднання виходів, номери яких відповідають 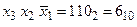; ; 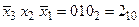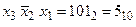, за допомогою елемента 3І-НІ.

Використаємо мікросхему К1533ЛЕ4 (або її зарубіжні аналоги – 7427PC, DM7427N, ECG7427, FLH621, MC7427N, SN7427N, SN66N). Принципова схема, яка реалізує вказані функції, зображена на рис. 2.21.

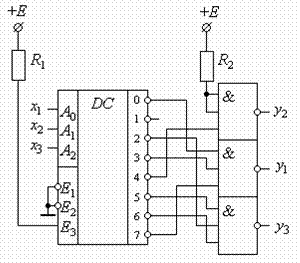
Рис.2.21.