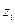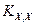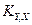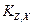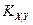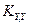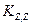ИЗМЕРЕНИЕ ТРАЕКТОРИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
1. ИЗМЕРИТЕЛЬНАЯ ТРАССА
Целый ряд задач, возникающих при летных испытаниях, требует знания траектории полета летательного аппарата. Траекторию самолета можно определить измерительными средствами, установленными на борту самолета или вне его. Практически, за редким исключением, траекторные измерения выполняют измерительными средствами, расположенными на Земле. В некоторых случаях измерительные средства размещаются на специально оборудованном летательном аппарате.
К траекторным измерительным средствам можно отнести:
· оптические (кинотеодолиты, фоторегистрирующие средства), обладающие высокой точностью измерений и применяемые при оценке взлетно–посадочных характеристик самолетов, аппаратуры слепой посадки, тарировки приемника воздушного давления (ПВД) и т.п.;
· радиотехнические (фазовые пеленгаторы, измерительные радиолокаторы), которые, уступая оптическим по точности измерений, имеют ряд достоинств и, в первую очередь, независимость от метеоусловий.
В состав измерительной трассы, кроме траекторных измерительных средств, входят приемные радиотелеметрические станции, системы единого времени (СЕВ), сбора и передачи измерительной информации с измерительных пунктов в вычислительный центр (ВЦ), связи и управления летным экспериментом.
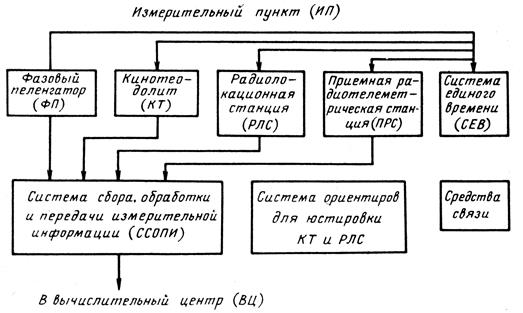
Отдельно расположенное измерительное средство или их группа с ориентирами и устройствами для юстировки измерительных средств, местной СЕВ, аппаратурой регистрации, первичной обработки, преобразования и передачи измерительной информации по линиям связи в ВЦ средствами связи образуют измерительный пункт (рис. 1).
|
Рис. 1. Схема измерительного пункта.
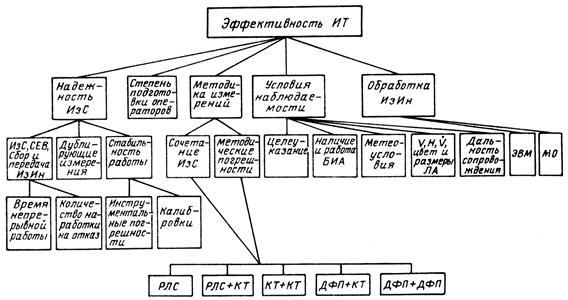
На измерительной трассе обычно находится несколько измерительных пунктов. Размеры (протяженность) измерительной трассы определяются типами испытываемых самолетов и задачами их испытаний. Измерительная трасса должна обеспечить при заданных условиях полета самолетов и их количества выполнение измерений с требуемой точностью, надежностью и эффективностью, которая зависит от целого ряда факторов (рис. 2).
|
Рис. 2. Факторы, влияющие на эффективность измерительной трассы.
Дальность действия измерительной трассы определяется дальностью действия отдельных измерительных пунктов, их количеством и размещением на измерительной трассе.
Под траекторией полета летательного аппарата понимается ряд последовательных положений его центра масс в пространстве в зависимости от времени. Летательный аппарат рассматривается при этом как материальная точка. Траектория представляется кривой, аппроксимирующей совокупность отсчетов текущих координат во времени.
Траекторные измерения являются косвенными измерениями. Измерительными средствами непосредственно определяются составляющие вектора положения летательного аппарата (или их совокупность) – дальность, углы визирования, косинусы направляющих углов (направляющие косинусы), называемые первичными параметрами. Состав первичных параметров определяет метод измерения траектории. По первичным параметрам рассчитывается траектория летательного аппарата в заданной системе координат согласно выражениям
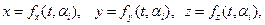
где 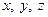 – текущие координаты траектории летательного аппарата, t – текущее время,
– текущие координаты траектории летательного аппарата, t – текущее время, 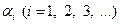 – текущее значение первичных параметров.
– текущее значение первичных параметров.
Система траекторных измерений состоит из следующих подсистем:
· наземных измерительных средств, измеряющих текущие значения первичных параметров траектории полета летательного аппарата, ориентиров для юстировки измерительных средств;
· бортовой аппаратуры или средств, необходимых для взаимодействия с наземными измерительными средствами или выполняющих измерения на летательном аппарате автономно;
· аппаратуры единого времени, создающей шкалу времени, обеспечивающую привязку к этой шкале всех измерений (измерительных средств трассы и летательного аппарата), а также выдачу импульсов с заданной частотой, необходимых для управления работой измерительных средств;
· аппаратуры преобразования, регистрации, предварительной обработки, сбора и передачи измерительной информации в ВЦ.
Система траекторных измерений должна обладать высокой точностью измерений первичных параметров и привязки их через СЕВ к другим видам измерений, обеспечивать непрерывное измерение траектории на всей трассе полетов летательных аппаратов или на отдельных ее участках, а также допускать оперативную обработку результатов измерений траектории в темпе времени с целью использования ее в системе управления летным экспериментом.
В зависимости от целей летных испытаний результаты траекторных измерений представляются в различных системах координат.
Системы координат. Геодезические (географические) координаты используются для точного определения места положения (привязки к местности), юстировочных ориентиров. При этом вводится понятие уровневой поверхности Земли, представляющей собой поверхность мирового океана (без волн, приливов и течений), мысленно продолженную в сторону суши так, чтобы она всюду пересекала отвесные линии под прямым углом. Геометрическое тело, ограниченное этой поверхностью, называется геоидом. Для территории России за поверхность геоида принята уровневая поверхность, проходящая через нуль кронштадского футштока. Первым приближением к поверхности геоида служит сферическая поверхность со средним радиусом, равным 6371 км. Такое представление формы Земли оказывается достаточным для решения многих практических задач летных испытаний. Вторым приближением к геоиду является референц–эллипсоид Красовского, который принят за модель Земли для всех геодезических работ, проводимых в России. Его большая (экваториальная) полуось а = 6 378 245 м; малая (полярная) полуось b = 6 356 863 м; полярное сжатие 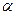 = 1 : 298,3; первый эксцентриситет е2 = 0,00669342; второй эксцентриситет (е’)2 = 0,00673853.
= 1 : 298,3; первый эксцентриситет е2 = 0,00669342; второй эксцентриситет (е’)2 = 0,00673853.
Геодезическими (географическими) координатами являются угловые величины, называемые долготой (L) и широтой (В), которые определяют положение точки земной поверхности относительно начального (Гринвичского) меридиана и экватора соответственно. Если координаты в такой системе получают при помощи геодезических измерений и последующих вычислений на поверхности референц–эллипсоида, то такие координаты называют геодезическими.
Геодезическая широта В – угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора. Геодезическая долгота L – двугранный угол между плоскостью начального (нулевого) меридиана и плоскостью меридиана данной точки. Координатными линиями служат параллели (широты) и меридианы (долготы), изображаемые на картах.
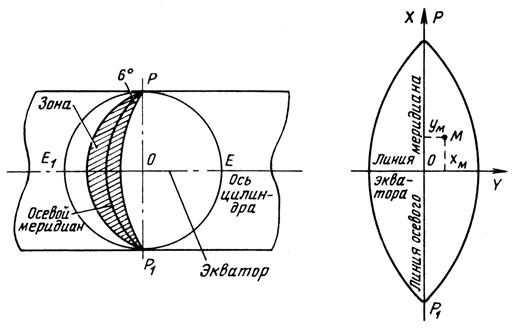
Координаты Гаусса–Крюгера используются при измерениях на небольших участках земной поверхности. Система координат при этом плоская и представляет собой проекцию земного эллипсоида на поверхность эллиптического цилиндра, а затем на плоскость. На один цилиндр проектируется зона земной поверхности, занимающая по долготе 60, следовательно, вся поверхность, Земли проектируется на 60 цилиндров. Каждый цилиндр касается земного эллипсоида по среднему меридиану зоны (рис. 3). Проекция Гаусса–Крюгера конформна, равноугольна, т.е. сохраняет на плоскости углы изображаемых фигур, равновелика – не искажает площади и равнопромежуточна, т.е. не искажает длины.
|
Рис. 3. Координаты Гаусса–Крюгера.
Поэтому ее можно практически считать планом. В каждой зоне осями прямоугольных координат служат средний меридиан зоны, изображаемый на плоскости осью абсцисс X, и экватор – осью Y. Гринвичский меридиан принят западным меридианом шестиградусной зоны № 1. Номера зон возрастают с запада на восток. Долгота шестиградусной зоны с номером N определится по формуле  .
.
Для каждой зоны вместо географической сетки (широты, меридианы) на проецируемой поверхности строят прямоугольную сетку координат, называемую координатами Гаусса–Крюгера. При пересчете прямоугольных координат (х, у) Гаусса–Крюгера в географические можно пользоваться следующими приближенными формулами:
 ,
,
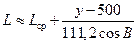 ,
,
где х и у в км.
Геоцентрическая система координат используется, в основном, как вспомогательная, дающая возможность пересчета координат летательного аппарата из одной системы в другую, например, из местной системы в любую прямоугольную, выбранную на земной поверхности. Кроме этого, если необходимо знать положение любой точки М, находящейся во внешнем пространстве Земли, пользуются геоцентрической центральной прямоугольной пространственной системой координат.
В этой системе за начало координат принимается центр референц–эллипсоида. Ось 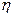 направлена по полярной оси эллипсоида, ось
направлена по полярной оси эллипсоида, ось 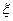 образуется пересечением плоскости меридиана Гринвича и плоскости экватора, ось
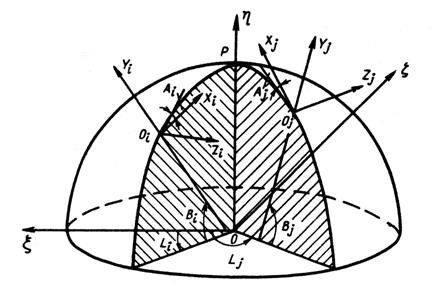
образуется пересечением плоскости меридиана Гринвича и плоскости экватора, ось 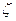 дополняет систему до правой (рис. 4).
дополняет систему до правой (рис. 4).
|
Рис. 4. Схема геоцентрических, географических и местных
прямоугольных координат.
Взаимосвязь между координатами точки в геоцентрической системе координат 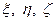 и географической – В и L выражается формулами:
и географической – В и L выражается формулами:
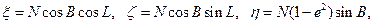
где 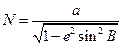 – длина нормали от точки М до пересечения с осью
– длина нормали от точки М до пересечения с осью 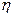 .
.
Присутствие в формулах длины нормали N дает возможность определить превышение точки М над референц–эллипсоидом. Увеличив длину нормали на высоту Н, получим значение координат точки М в геоцентрической системе с учетом превышения данной точки (пункта) над уровнем моря:
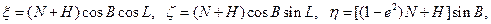
В практике трассовых измерений для непосредственного наблюдения за летательным аппаратом пользуются прямоугольными системами координат. Для предварительного выбора направления осей координат (местных и трассовых), расположения измерительных пунктов, отсчета расстояний и т.п. используют географические карты в проекции Гаусса–Крюгера, которые можно рассматривать как план местности зоны полетов аэродрома. Точная привязка (не хуже 3 класса) начал местных и трассовых координат, ориентиров и т.п. выполняется топографической службой.
Траектория полета летательного аппарата должна быть представлена в такой системе координат, которая не требует сложных пересчетов при подготовке к анализу результатов испытаний. В связи с тем, что каждый измерительный пункт может измерять траекторию летательного аппарата на ограниченном участке, траекторные измерения выполняются ими в местной системе прямоугольных координат с началом в определенной точке данного измерительного пункта. Обычно за начало местной системы координат принимают точку фокуса кинотеодолита (КТ), находящего на измерительном пункте. Если для траекторных измерений применяется радиолокационная станция, то за начало координат принимают центр параболоида ее антенны, а если фазовый пеленгатор – то центр антенного поля. Направление оси X местной системы координат для оптических измерительных средств и радиолокационной станции выбирается на север, для фазовых пеленгаторов – по одной из осей антенного поля. Ось Y направлена вверх перпендикулярно к поверхности эллипсоида Красовского. Ось Z дополняет систему координат до правой.
Если траекторные измерения выполняются несколькими измерительными пунктами, то их результаты представляются в единой трассовой системе координат, начало которой должно быть точно определено геодезической привязкой. Направление оси X трассовой системы координат можно выбрать вдоль основной взлетно–посадочной полосы или вдоль направления интенсивных испытательных полетов. Направление осей Y и Z такое же, как и для местной системы координат. На рис. 5 приведена схема трассовой и местных систем координат.
|
Рис. 5. Схема трассовых и местных координат.
Координаты 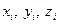 одной прямоугольной системы пересчитываются в другую, имеющую координаты х, у, z, поворотом осей на угол между ними с последующими переносом начала координат Оi одной системы в начало – О другой.
одной прямоугольной системы пересчитываются в другую, имеющую координаты х, у, z, поворотом осей на угол между ними с последующими переносом начала координат Оi одной системы в начало – О другой.
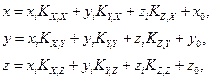
где 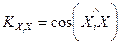 – направляющий косинус между осями Xi и X;
– направляющий косинус между осями Xi и X; 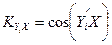 – то же между осями Yi и Х и т.д.;
– то же между осями Yi и Х и т.д.; 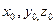 – старые координаты нового начала. Можно также пользоваться уравнениями, полученными путем смещения осей в новое начало, а после этого их поворотом.
– старые координаты нового начала. Можно также пользоваться уравнениями, полученными путем смещения осей в новое начало, а после этого их поворотом.
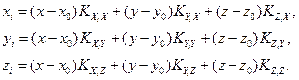
|
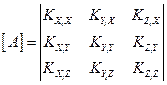
Рекомендуется следующая последовательность пересчета координат начала одной системы в другую и направляющих косинусов между осями координат (при этом используется геоцентрическая система координат):
· вычисление положения начала (Оi) координат местной системы OiXiYiZi в геоцентрической системе 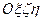 ;
;
· вычисление координат начала (О) геоцентрической системы в местной системе OjXjYjZj;
· определение направляющих косинусов между осями местных систем XiYiZi XjYjZj и осями геоцентрической системы  ;
;
· перенос координат из одной системы XiYiZi в другую XjYjZj.
Положение начала Оi местной системы координат в геоцентрической определяется уравнениями связи между геоцентрической и геодезической системами координат с у четом превышения (Hi) точки Оi над поверхностью эллипсоида.
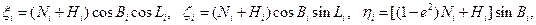
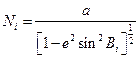
Здесь 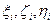 – координаты точки Оi в геоцентрической системе координат.
– координаты точки Оi в геоцентрической системе координат.
Координаты начала (О) геоцентрической системы в местной системе координат определяются следующими выражениями:

При этом полагается, что начало системы координат XjYjZj находится в точке Oj с геодезическими координатами Lj, Вj; ось ОjYj направлена по нормали к поверхности референц–эллипсоида, ось OjXj направлена по азимуту Aj, отсчитываемому по часовой стрелке из пункта наблюдения от северного направления до направления визирования на объект.
Для вычисления направляющих косинусов между осями местной системы XjYjZj и осями  геоцентрической системы координат привлекаются выражения, определяющие координаты
геоцентрической системы координат привлекаются выражения, определяющие координаты 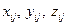 точки Оi в системе координат ХjYjZj:
точки Оi в системе координат ХjYjZj:
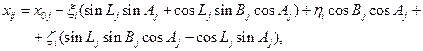

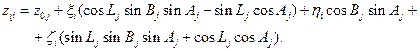
В этих выражениях коэффициенты при  являются постоянными для каждой координатной системы. Обозначив их буквой
являются постоянными для каждой координатной системы. Обозначив их буквой 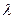 с соответствующими индексами, имеем:
с соответствующими индексами, имеем:
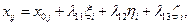
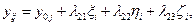
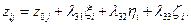
Коэффициенты 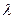 представляют собой направляющие косинусы между осями геоцентрической системы координат и осями системы XjYjZj, которые можно представить таблицей
представляют собой направляющие косинусы между осями геоцентрической системы координат и осями системы XjYjZj, которые можно представить таблицей

| 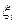
| 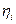
| 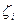
|
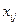
| 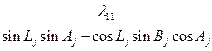
| 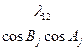
| 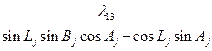
|
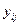
| 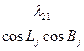
| 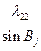
| 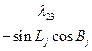
|
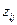
| 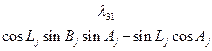
| 
| 
|
Система уравнений и таблица направляющих косинусов 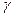 между осями геоцентрической системы и системы ХiУiZi аналогичны и отличаются только индексами – вместо j индекс i.
между осями геоцентрической системы и системы ХiУiZi аналогичны и отличаются только индексами – вместо j индекс i.
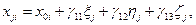
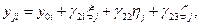
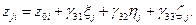

| 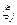
| 
| 
|
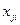
| 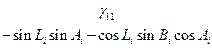
| 
| 
|
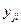
| 
| 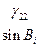
| 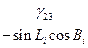
|
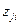
| 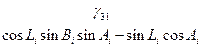
| 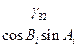
| 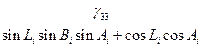
|
Значения координат x0i, y0i, z0i центра референц–эллипсоида в системе XiYiZi описываются формулами
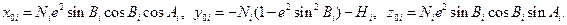
Для переноса координат траектории из одной местной прямоугольной системы координат в другую, местную прямоугольную привлекаются:
· матрица направляющих косинусов 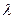 между осями
между осями  и XjYjZj;
и XjYjZj;
· матрица направляющих косинусов 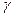 между осями
между осями  и XiYiZi;
и XiYiZi;
· координаты начала системы XiYiZi в системе координат XjYjZj, которые мы обозначим 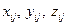 ;
;
· координаты начала системы XjYjZj в системе координат XiYiZi, которые мы обозначим –  ;
;
· координаты начала геоцентрической системы в местных системах координат – 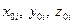 ;
; 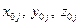 ;
;
· координаты начала местных систем координат в геоцентрической системе координат –  ;
; 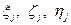 .
.
Преобразование координат из одной прямоугольной системы в другую состоит в параллельном переносе осей координат в новую точку, а затем в двойном повороте осей в соответствии с матрицами 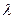 и
и 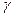 .
.
Если обозначить 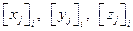 – координаты
– координаты 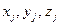 объекта в системе координат
объекта в системе координат 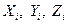 , то преобразования координат производятся по формулам
, то преобразования координат производятся по формулам

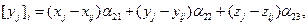 (А)
(А)
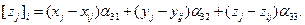
Таблица значений 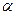 имеет вид
имеет вид

| 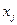
| 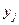
| 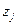
|
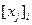
| 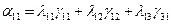
| 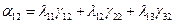
| 
|
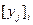
| 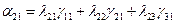
| 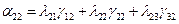
| 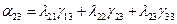
|
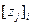
| 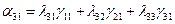
| 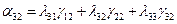
| 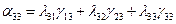
|
Коэффициенты 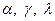 величин
величин 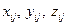 и
и 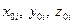 , а также
, а также 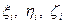 для каждой пары координатных систем (для каждых двух измерительных пунктов) постоянны. Они вычисляются заранее и преобразование координат сводится к решению уравнения (А).
для каждой пары координатных систем (для каждых двух измерительных пунктов) постоянны. Они вычисляются заранее и преобразование координат сводится к решению уравнения (А).
Если при траекторных измерениях из одного измерительного пункта одновременно измеряют дальность – D, азимуты – 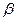 и углы места –
и углы места – 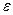 , то результаты измерений, непосредственно получаемые в полярных координатах (рис. 6), преобразуются в прямоугольные по следующим формулам:
, то результаты измерений, непосредственно получаемые в полярных координатах (рис. 6), преобразуются в прямоугольные по следующим формулам:
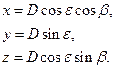
|
Рис. 6. Схема полярных координат.
Дата добавления: 2020-10-14; просмотров: 1071;