СХЕМИ ЕЛЕКТРОННОГО ПІДПИСУ

Розглянемо тепер приклад практичної схеми електронного підпису зі схемою аутентифікації Шнорра. У цьому протоколі інтерактивність потрібна тільки для того, щоб одержати випадковий запит від того, що 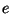перевіряє. Тому якби в того, що доводить було надійне джерело випадковості, що користається довірою у того, що перевіряє, то протокол можна було б зробити не інтерактивним. Фіат і Шамір запропонували спосіб перетворення протоколу аутентифікації в схему електронного підпису шляхом заміни випадкового запиту деяким «сурогатом». А саме, нехай 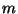- повідомлення, того, хто підписується, 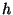- криптографічна хеш-функція. Тоді замість звертання до того, що перевіряє (він же - одержувач повідомлення) той, що доводить (він же - Той, хто підписує) обчислює величину 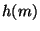і використовує її як запит 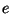. Цей метод універсальний, тому що може бути застосований до широкого класу протоколів аутентифікації. Опишемо тепер одержувану в результаті такого перетворення схему електронного підпису Шнорра. Відкритий і таємний ключі тим, хто підписує генеруються в цій схемі в такий же спосіб, як у схемі аутентифікації Шнорра. Відкритий ключ міститься в загальнодоступному сертифікованому довіднику.

1. Той, хто підписує вибирає випадкове число 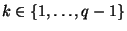й обчислює .

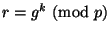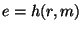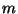2. Той, хто підписує обчислює , де - повідомлення, Той, хто підписується.

3. Той, хто підписує обчислює 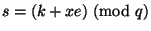і посилає повідомлення 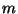із підписом 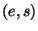одержувачу.

4. Одержувач обчислює 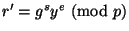і перевіряє, чи виконується рівність 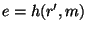. Якщо так, то підпис правильний, у противному випадку - відкидається.

Передбачається, що хеш-функція 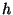відображає пари значень 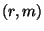у множину .

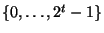Легко перевірити, що для підпису, генерованого відповідно до протоколу, перевірка п.4 завжди буде виконана.

Стійкість схеми Шнорра в значній мірі залежить від властивостей функції 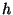. Якщо супротивник уміє відшукувати колізії спеціального виду, тобто по заданій парі 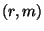знаходити інше повідомлення 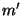, , 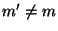таке, що 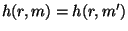, то він може здійснювати екзистенційну підробку підписів. Для цього досить перехопити повідомлення 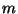і підпис 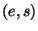для нього, а також знайти колізію зазначеного виду. Тоді пари 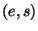буде також підписом і для повідомлення .

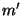Хеш-функція є невід’ємною частиною конструкції схем електронного підпису. Це є наслідком необхідності підписувати повідомлення різної довжини. Звичайно, довгі повідомлення можна розбивати на блоки, що мають необхідну для схеми підпису довжину, і підписувати кожен блок. Але це рішення неефективне. На практиці використовуються хеш-функції, що перетворюють повідомлення довільної довжини в хеш-значення необхідної довжини. Ясно, що така хеш-функція повинна бути в якомусь сенсі стійкою проти спроб знайти колізії. Але оскільки практичні хеш-функції конструюються для конкретних довжин хеш-значень (скажемо, 256 бітів), формалізувати цю вимогу не вдається.

На відміну від протоколів аутентифікації, для практичних схем електронного підпису невідомі методи доказу стійкості. Стійкі схеми підпису не можуть бути доказами з нульовим розголошенням. Це легко зрозуміти, якщо згадати, що визначення нульового розголошення вимагає існування моделюючої машини, що, не знаючи таємного ключа, створює для усіх величин, що спостерігаються що перевіряє, розподіл імовірностей, невідрізнимий від того, який виникає при виконанні протоколу. Але усе, що бачить той, що перевіряє (він же - одержувач) у процесі виконання протоколу, це - повідомлення з підписами. Отже, моделююча машина, якщо вона існує, може підробляти підпис, тому що створювані нею «підписи» повинні бути невідрізнимі від справжніх, зокрема, і для алгоритму перевірки підписів.

Стійкість схем електронного підпису проти пасивного супротивника, що, знає тільки відкритий ключ і намагається підробляти підпис, може бути доведена в так званій моделі з випадковим оракулом. У цій моделі той, хто підписує і перевіряє замість обчислення функції 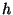звертаються до оракула, що для кожного вхідного значення 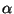вибирає випадкове вихідне значення 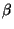і видає його як відповідь. При цьому пара 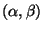запам’ятовується й у випадку повторного звертання з вхідним значенням 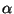оракул знову видасть значення 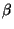. Як помітили Фіат і Шамір, ідея доказу коректності схем аутентифікації може бути застосована в даній моделі для доказу стійкості схем підпису проти пасивного супротивника. Цей результат справедливий для широкого класу схем підпису, що включає схему Шнорра. Фактично це означає, що схеми підпису є стійкими (проти зазначеного вище пасивного супротивника), якщо хеш-функція поводиться, як випадкова функція. Це твердження є по суті єдиним результатом теоретичної криптографії, що стосується стійкості практичних схем електронного підпису.

Таким чином використання цифрового підпису забезпечує:

- по-перше, можливість ідентифікації приналежності підпису на основі об’єктивних показників;

- по-друге, високу захищеність від підробки;

- по-третє, це твердий зв’язок із документом, що підписується.

Якщо перші дві переваги ще можна реалізувати для традиційного підпису, то виконання третього можливе тільки у випадку застосування електронного цифрового підпису(ЕЦП ). Питання про застосування інших аналогів власноручного підпису виходить за рамки розглянутої тематики.

Виконання всіх трьох вимог стає можливим виходячи із самої природи ЕЦП. ЕЦП є деяке досить довге число, отримане в результаті перетворення електронного образу документа, що захищається, із використанням секретного (особистого) ключа відправника. Будь-хто може перевірити ЕЦП під документом за допомогою відповідних перетворень із використанням, знову таки, електронного образу документа, відкритого (публічного) ключа відправника і власне значення ЕЦП. Відкритий і Таємний ключі однозначно зв’язані між собою, однак неможливо обчислити Таємний ключ за відкритим. Точніше, якщо формулювати зовсім строго, то в даний момент не знайдено алгоритмів, що дозволяють здійснити таке обчислення за прийнятний час, з урахуванням сучасного рівня розвитку обчислювальної техніки і використовуваної довжини ключів.

Таємний ключ зберігається в таємниці і відомий тільки власнику, ніхто, крім власника не зможе сформувати ЕЦП під документом. Зате кожний може перевірити (за допомогою доступного усім відкритого ключа), що документ підписав саме власник, і що документ не перекручений (тому що значення ЕЦП залежить і від умісту документа). Логічний наслідок полягає в тому, що просто перенести ЕЦП із одного документа на інший (за аналогією з ксерокопіюванням чи скануванням звичайного підпису на паперовому документі, чи використанням факсиміле) неможливо. Таким чином, можна сказати, що ЕЦП є реквізитом даного конкретного електронного документа.

Алгоритм RSA.

Алгоритм RSA стоїть біля витоків джерел асиметричної криптографії. Він був запропонований трьома дослідниками-математиками Рональдом Рівестом (R. Rivest) , Аді Шаміром (A. Shamir) і Леонардом Адльманом (L. Adleman) у 1977-78 роках.

Першим етапом будь-якого асиметричного алгоритму є створення пари ключів: відкритого і закритого та поширення відкритого ключа “в усьому світі”. Для алгоритму RSA етап створення ключів складається з наступних операцій:

1. Вибираються два простих (!) числа p та q

2. Обчислюється їхній добуток n(=p*q)

3. Вибирається довільне число e (e<n), таке, що НОД(e,(p-1)(q-1))=1, тобто e повинно бути взаємно простим із числом (p-1)(q-1).

4. Методом Евкліда зважується в цілих числах (!) рівняння e*d+(p-1)(q-1)*y=1. Тут невідомими є змінні d та y – метод Евкліда саме і знаходить множину пар (d, y), кожна з яких є рішенням рівняння в цілих числах.

5. Два числа (e, n) – публікуються як відкритий ключ.

6. Число d зберігається в найсуворішій таємниці – це і є закритий ключ, що дозволить читати всі послання, зашифровані за допомогою пари чисел (e, n).

Як же здійснюється власне шифрування за допомогою цих чисел:

1. Відправник розбиває своє повідомлення на блоки, рівні k = [log₂(n)] біт, де квадратні дужки позначають узяття цілої частини від дробового числа.

2. Подібний блок, як Ви знаєте, може бути інтерпретований як число з діапазону (0; 2^k-1). Для кожного такого числа (назвемо його m_i) обчислюється вираження c_i=((m_i)^e)mod n. Блоки c_i і є зашифроване повідомлення Їх можна спокійне передавати по відкритому каналі, оскільки операція підняття в степінь по модулі простого числа, є необоротною математичною задачею. Зворотна їй задача зветься “логарифмування в скінченому полі” і є на кілька порядків більш складною задачею. Тобто навіть якщо зловмисник знає числа e і n, те по c_i прочитати вихідні повідомлення m_i він не може ніяк, крім як повним перебором m_i.

А от на прийомній стороні процес дешифрування все-таки можливий, і допоможе нам у цьому збережене в таємниці число d. Досить давно була доведена теорема Ейлера, окремий випадок якої стверджує, що якщо число n представимо у вигляді двох простих чисел p і q, то для будь-якого x має місце рівність (x^(p-1)(q-1))mod n = 1. Для дешифрування RSA-повідомлень скористаємося цією формулою.

Піднімемо обидві її частини до степені (-y): (x^{(-y)(p-1)(q-1)})mod n = 1^(-y) = 1. Тепер помножимо обидві частини на x: (x^{(-y)(p-1)(q-1)+1})mod n = 1*x = x.

А тепер згадаємо як ми створювали відкритий і закритий ключі. Ми підбирали за допомогою алгоритму Евкліда d таке, що e*d+(p-1)(q-1)*y=1, тобто e*d=(-y)(p-1)(q-1)+1. А отже в останньому виразі попереднього абзацу ми можемо замінити показник степені на число (e*d). Одержуємо (x^e*d)mod n = x. Тобто для того щоб прочитати повідомлення c_i=((m_i)^e)mod n досить звести його в степінь d за модулем m: ((c_i)^d)mod n = ((m_i)^e*d)mod n = m_i.

Насправді операції підняття до степені великих чисел досить трудомісткі для сучасних процесорів, навіть якщо вони здійснюються за оптимізованими за часом алгоритмами. Тому звичайно весь текст повідомлення кодується звичайним блоковим шифром (набагато більш швидким), але з використанням ключа сеансу, а от сам ключ сеансу шифрується саме асиметричним алгоритмом за допомогою відкритого ключа одержувача і поміщається в початок файлу.

Питання для самоконтролю

1. В чому полягає захист інформації від несанкціонованого доступу?

2. Що вивчає наука криптографія?

3. Дайте характеристику симетричних криптографічних систем.

4. Охарактеризуйте асиметричні криптографічні системи.

5. Що таке електронний цифровий підпис?

6. Чим регулюється правове забезпечення електронного цифрового підпису в Україні?

7. Для чого призначена сертифікація ключів?

8. У чому полягає процедура аутентифікації та авторизації користувачів?

9. Які вимоги ставляться до паролів?

10. Комп’ютерні віруси та антивірусні програми.

11. Програмні засоби захисту та резервування інформації

ТЕМА 7