Електронний цифровий підпис

Для виключення можливості модифікації початкового повідомлення або підміни цього повідомлення іншим необхідно передавати повідомлення разом з електронним підписом. Електронний цифровий підпис - це послідовність символів, отримана в результаті криптографічного перетворення початкового повідомлення з використанням закритого ключа і що дозволяє визначати цілісність повідомлення і приналежність його авторові за допомогою відкритого ключа. Іншими словами повідомлення, зашифроване за допомогою закритого ключа, називається електронним цифровим підписом.

Відправник передає незашифроване повідомлення в початковому вигляді разом із цифровим підписом. Одержувач за допомогою відкритого ключа розшифровує набір символів повідомлення з цифрового підпису і порівнює їх з набором символів незашифрованого повідомлення. При повному збігу символів можна стверджувати, що отримане повідомлення не модифіковане і належить його авторові.

Розглянемо тепер приклад практичної схеми електронного підпису зі схемою аутентифікації Шнорра. У цьому протоколі інтерактивність потрібна тільки для того, щоб одержати випадковий запит 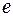від того, хто перевіряє. Тому якби в того, що доводить було надійне джерело випадковості, що користається довірою у того, що перевіряє, то протокол можна було б зробити не інтерактивним. Фіат і Шамір запропонували спосіб перетворення протоколу аутентифікації в схему електронного підпису шляхом заміни випадкового запиту деяким «сурогатом». А саме, нехай 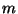- повідомлення, того, хто підписується, 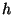- криптографічна хеш-функція. Тоді замість звертання до того, що перевіряє (він же - одержувач повідомлення) той, що доводить (він же - Той, хто підписує) обчислює величину 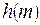і використовує її як запит 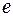. Цей метод універсальний, тому що може бути застосований до широкого класу протоколів аутентифікації. Опишемо тепер одержувану в результаті такого перетворення схему електронного підпису Шнорра. Відкритий і таємний ключі тим, хто підписує генеруються в цій схемі в такий же спосіб, як у схемі аутентифікації Шнорра. Відкритий ключ міститься в загальнодоступному сертифікованому довіднику.

1. Той, хто підписує вибирає випадкове число 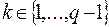й обчислює .

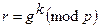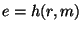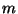2. Той, хто підписує обчислює , де - повідомлення, Той, хто підписується.

3. Той, хто підписує обчислює 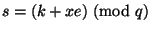і посилає повідомлення 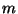із підписом 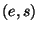одержувачу.

4. Одержувач обчислює 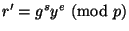і перевіряє, чи виконується рівність 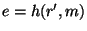. Якщо так, то підпис правильний, у противному випадку - відкидається.

Передбачається, що хеш-функція 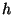відображає пари значень 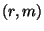у множину .

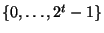Легко перевірити, що для підпису, генерованого відповідно до протоколу, перевірка п.4 завжди буде виконана.

Стійкість схеми Шнорра в значній мірі залежить від властивостей функції 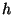. Якщо супротивник уміє відшукувати колізії спеціального виду, тобто за заданою парою 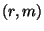знаходити інше повідомлення 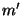, , 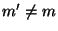таке, що 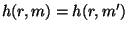, то він може здійснювати екзистенційну підробку підписів. Для цього досить перехопити повідомлення 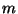і підпис 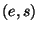для нього, а також знайти колізію зазначеного виду. Тоді пари 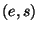буде також підписом і для повідомлення .

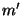Хеш-функція є невід’ємною частиною конструкції схем електронного підпису. Це є наслідком необхідності підписувати повідомлення різної довжини. Звичайно, довгі повідомлення можна розбивати на блоки, що мають необхідну для схеми підпису довжину, і підписувати кожен блок. Але це рішення неефективне. На практиці використовуються хеш-функції, що перетворюють повідомлення довільної довжини в хеш-значення необхідної довжини. Ясно, що така хеш-функція повинна бути в якомусь сенсі стійкою проти спроб знайти колізії. Але оскільки практичні хеш-функції конструюються для конкретних довжин хеш-значень (скажемо, 256 бітів), формалізувати цю вимогу не вдається.