Коэффициенты заполнения катушки и обмотки.

Очевидно, что в любой катушке площадь сечения меди из-за наличия воздушных прослоек и изоляции всегда меньше, чем общая площадь сечения катушки. Отношение этих площадей называется коэффициентом заполнения катушки

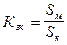, (250)

где S_м и S_к – площади сечения меди и катушки.

Для катушки цилиндрической

Рис. 112. Размеры катушки формы (рис. 112) из круглого провод

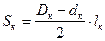, . (251)

Подставляя в коэффициент заполнения катушки, получим

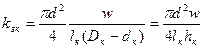, (252)

,

где d – диаметр голого провода, см; w – число витков обмотки.

Коэффициент заполнения катушки зависит от многих факторов: профиля сечения провода, толщины и вида изоляции провода и катушки, качества намотки, диаметра провода и т. д. Если при определении площади катушки не учитывать толщину внешней изоляции (каркас, бандаж), то получим коэффициент заполнения обмотки

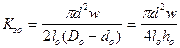, (253)

где 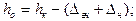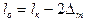; 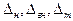– толщина изоляции наружной, внутренней и торцевой поверхностей катушки, см.

Связь между коэффициентами заполнения катушки и обмотки следующая

. (254)

Коэффициент заполнения обмотки всегда больше коэффициента заполнения катушки. Он зависит от качества укладки, диаметра провода и толщины межслойной изоляции. Если качество укладки учесть коэффициентом К_у, то можно выразить коэффициент заполнения обмотки так: а) для круглого провода без

Рис. 113. К определению К_зо межслойной изоляции

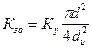, (255)

d_и – диаметр провода с изоляцией, см.

б) для круглого провода с межслойной изоляцией (рис.113, б).

Таким образом, коэффициент заполнения обмотки есть отношение площади, занимаемой медью к площади квадрата на рис.113

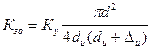, (256)

где 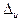– толщина межслойной изоляции.

Коэффициент укладки зависит от способа намотки обмотки. Различают три вида намотки:

1) неравномерная (дикая) намотка, которая производится без специальных приспособлений для укладки витков, коэффициент укладки равен К_у = 0,7…0,9;

2) рядовая намотка, при которой витки одного слоя укладываются плотно друг к другу, а витки двух смежных слоев располагаются один над другим; для такой намотки (рис. 113, а) К_у = 0,9…0,95;

3) шахматная намотка, при которой витки верхнего слоя укладываются в промежутки между витками нижнего слоя (рис. 114)

К_у = 0,95…1,05.

Коэффициент заполнения обмотки зависит

от соотношения толщины изоляции и

Рис. 114. Шахматная намотка толщины провода

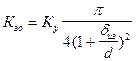при 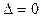. (257)

Здесь – толщина витковой изоляции;

Отношение 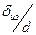уменьшается с увеличением d, поэтому, К_зо с ростом диаметра провода увеличивается и зависит от марки провода, от качества намотки (через К_у), от натяжения провода, настройки намоточного станка, от наличия междуслойных прокладок.

Значения коэффициента заполнения обмотки от различных факторов приводятся в справочной литературе.

Параметры катушки

К параметрам катушки относятся активное и индуктивное сопротивление для катушек переменного тока и оммическое сопротивление катушек постоянного тока.

Активное или оммическое сопротивление

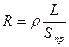, (258)

где 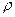– удельное сопротивление материала провода; 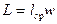– общая длина провода катушки; 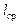– средняя длина витка катушки; w – число витков катушки; 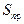– площадь сечения провода.

Средняя длина витка определяется в зависимости от конструкции катушки так: 1) для катушки цилиндрической формы

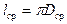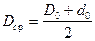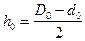; ; ; (259)

2) для катушки прямоугольной формы (рис. 115)

, (260)

где а₀, b₀ и h₀ – размеры обмотки (без каркаса).

Итак, активное сопротивление катушки будетравно

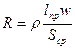. (261)

Удельное сопротивление материала провода ρ принимается

равным значению, соответствующему рабочей температуре катушки, если сопротивление катушки определяестя в нагретом состоянии.

Иногда сопротивление катушки выражают через размеры обмотки, например, ;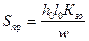

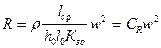, (262)

где 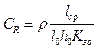– активное сопротивление

катушки, приведенное к одному витку.

Индуктивное сопротивление катушки

или 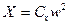, (263)

где C_x = ωG_м – индуктивное сопротивление, Рис. 115. Прямоугольная приведенное к одному витку; 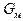– магнитная

катушка проводимость магнитной цепи.

Расчет катушек

В результате расчета магнитной цепи определяется магнитный поток, создаваемый катушкой или ее намагничивающей силой. Катушка должна быть рассчитана таким образом, чтобы, с одной стороны, обеспечить требуемую намагничивающую силу, а с другой – максимальная температура обмотки не превышала допустимую температуру для данного класса нагревостойкости изоляции. Это условие обеспечивается соответствующим выбором размеров катушки.

Катушки постоянного тока

А) Расчет параллельной катушки. Для расчета катушки должны быть заданы: размеры окна под обмотку (из проектного расчета электромагнита), намагничивающая сила (из расчета магнитной цепи) и напряжение питания. Необходимо определить площадь сечения провода S_пр, число витков катушки w, сопротивление R, ток I, мощность потерь P, перегрев .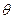

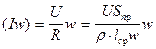, (264)

отсюда, 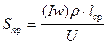, (265)

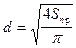. (266)

После этого по таблице стандартных проводов выбирается ближайший больший диаметр провода и уточняется площадь сечения провода. Определяется коэффициент заполнения обмотки по графикам, по таблицам или по формуле с учетом марки провода. Затем определяется число витков обмотки

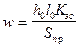, где h₀ и l₀ – размеры обмотки по рис. 112.

Определяется сопротивление , (267)

ток 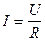, намагничивающая сила ,

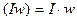мощность 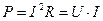. (268)

Перегрев обмотки над температурой окружающей среды

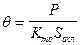, (269)

где К_то – коэффициент теплоотдачи с поверхности катушки; S_охл – поверхность охлаждения.

При изменении питающего напряжения и сохранении размера окна под обмотку должно иметь место равенство

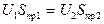, (270)

так как 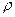и 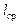остаются неизменными. При этом намагничивающая сила останется также неизменной. Поскольку при переходе от одного напряжения на другое изменяется диаметр провода (а следоательно, толщина изоляции), коэффициент заполнения обмотки также меняется в следующем соотношении

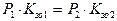. (271)

Если U₁ < U₂, то при переходе от напряжения U₁ на напряжение U₂ диаметр провода уменьшается. При меньшем диаметре провода из-за возросшей относительной толщины изоляции коэффициент заполнения обмотки уменьшается. Следовательно, при переходе на более высокое напряжение мощность, потребляемая катушкой, увеличивается.

Б) Расчет последовательной катушки.

Для расчета последовательной катушки должно быть задано: намагничивающая сила (Iw), размеры окна под обмотку h₀ и l₀, ток I. Рассчитать: площадь сечения провода, диаметр провода, число витков.

; ; .

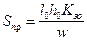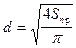Здесь коэффициентом заполнения обмотки предварительно задаются и уточняют его методом последовательных приближений.

Если размеры катушки неизвестны, то можно сечение провода найти через плотность тока, задаваясь ею в пределах j = 2…4 A/мм² для продолжительного режима работы, или j = 10 А/мм² – для кратковременного.

Расчет мощности и превышения температуры производится так же, как и для параллельной катушки.

Катушки переменного тока.

А) Расчет параллельной катушки.

Исходными данными для расчета параллельной катушки являются амплитуда намагничивающей силы, амплитуда потока и напряжения.

Уравнение равновесия напряжения на катушке можно записать так

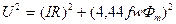. (272)

Так как активное падение напряжения в параллельных катушках значительно меньше реактивного, то в начале расчета можно положить IR = 0. Тогда, число витков обмотки равно

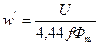, (273)

где f – частота сети.

Так как при расчете числа витков пренебрегается активным падением напряжения, действительное число витков должно быть несколько меньше и определяется по уравнению

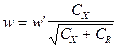, (274)

где , .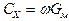

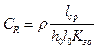Ток определяется из выражения 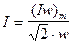. (275)

Коэффициент заполнения обмотки задается предварительно.

Площадь сечения провода

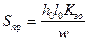, диаметр провода .

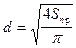Выбрав стандартный диаметр провода и его марку (т.е., изоляцию), а также способ укладки К_у, толщину межслойной изоляции (если необходимо), уточняют коэффициент заполнения обмотки, сечение S_пр и диаметр провода d_пр.

.

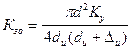Сопротивление обмотки: активное 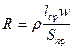, индуктивное 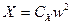, результирующее 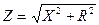. (276)

Б) Расчет последовательной катушки.

Если полное сопротивление обмотки электромагнита переменного тока Z при любом значении воздушного зазора меньше полного сопротивления цепи (последовательная катушка), то величина тока в обмотке не зависит от положения якоря. Расчет таких обмоток ведется также, как и для последовательных обмоток постоянного тока. Закон изменения потока в рабочем зазоре такого электромагнита аналогичен закону в электромагните постоянного тока, поскольку электромагнит работает при постоянной намагничивающей силе катушки.

Если электромагнит с параллельной катушкой питается от источника с другим напряжением и сила тяги должна остаться той же, то обмоточные данные должны быть соответственно изменены. Величина намагничивающей силы и угол сдвига между током и напряжением при этом считаются неизменными. Должны быть соблюдены следующие соотношения

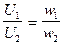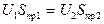, , , (277)

где S₀₁ и S₀₂ – площади окон под обмотку.

Полная мощность обмотки при переходе с одного напряжения на другое, при соблюдении указанных условий, не изменяется так как .

Вопросы для самоконтроля

8.5.1. Достоинства бескаркасных катушек электромагнитов.

8.5.2. Факторы, влияющие на коэффициент заполнения обмотки.

8.5.3. Что относится к параметрам катушки и как они определяются?

8.5.4. Порядок расчета катушек постоянного тока параллельного включения.

8.5.5. Особенности расчета катушек электромагнитов переменного тока.

8.5.6. Сравнить поверхности охлаждения каркасной и бескаркасной катушек.

8.5.7. Чем отличаются катушки последовательного и параллельного включения?

8.5.8. Что должно быть задано для расчета последовательной катушки?

8.5.9. Способы намотки катушек электрических аппаратов.

8.5.10. Достоинства и недостатки каркасных и бескаркасных катушек.

8.6. Примеры расчета [6]

8.6.1. Рассчитать катушку электромагнита постоянного тока, изображенную на рис. 104 по следующим размерам:

l_к = 5 см; d_к = 2 см; D_к =4 см; ∆_из = 0,1 см.

Напряжение катушки U_к = 110 В; намагничивающая сила (Iw) = 840 А.

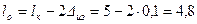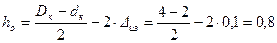Решение.Размеры обмотки: см;

см.

Выразим намагничивающую силу через напряжение и сопротивление катушки

.

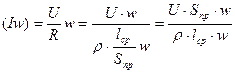Отсюда найдем площадь сечения провода

,

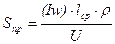Здесь ρ = 0,0224 Ом∙мм²/м – удельное сопротивление меди; 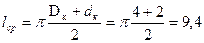см или l_ср = 0,094 м – средняя длина витка обмотки.

Тогда, 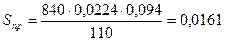мм².

Диаметр провода мм.

По таблице стандартных проводов [6] выбираем марку провода ПЭВ и ближайший больший диаметр d_пр = 0,15 мм, d_из = 0,18 мм, S_пр = 0,0176 мм².

Коэффициент заполнения обмотки

.

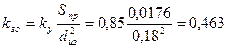здесь k_у = 0,85 – коэффициент укладки.

Число витков обмотки .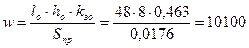

Сопротивление обмотки 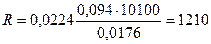Ом.

Ток катушки А.

Уточняем намагничивающую силу 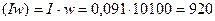А.

Мощность потерь 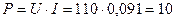Вт.

Плотность тока 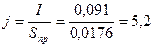А/мм².

8.6.2. Рассчитать катушку электромагнита переменного тока (рис.116) по данным задачи 8.6.1.

Рис. 116. Катушка электромагнита

Для расчета катушки электромагнита принимаем: катушка каркасная, намотана медным проводом рядовой намоткой с междуслойной изоляцией конденсаторной бумагой толщиной ∆_из = 0,05 мм; а = 2,5 см; b = 2,5 см; l_к = 5 см; h_к = 1,5 см; 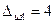мм – двух сторонняя толщина изоляции катушки в осевом направлении; мм – двух сторонняя толщина изоляции катушки в радиальном направлении.

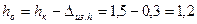Размеры обмотки см;

см.

Средняя длина витка обмотки

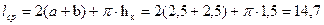см.

Индуктивное сопротивление обмотки, приведенное к одному витку

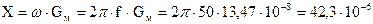Ом.

Активное сопротивление обмотки, приведенное к одному витку

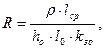
здесь 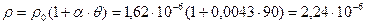Ом. см – удельное сопротивление меди при температуре 90 ^оС; k_зо = 0,5 – предварительный коэффициент заполнения обмотки (задаемся).

Тогда, Ом.

Число витков обмотки

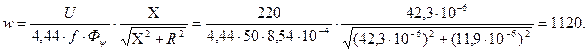Площадь сечения провода

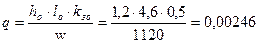см² или мм².

Диаметр провода

мм.

По таблице стандартных проводов [6] выбираем марку провода ПЭВ-2 сечением ближайшим большим расчетному q’ = 0,273 мм² и диаметром без изоляции d’ = 0,59 мм. Диаметр провода с изоляцией d_из = 0,66 мм.

Принимаем коэффициент укладки к_у = 0,93.

Уточняем коэффициент заполнения обмотки

.

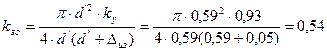Активное сопротивление обмотки

Ом.

Индуктивное сопротивление обмотки

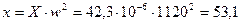Ом.

Полное сопротивление обмотки

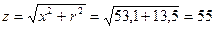Ом.

Ток в обмотке электромагнита

А.

МДС катушки 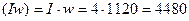А.

Мощность активных потерь Вт.