Основные расчетные зависимости
Тτечение жидкости по трубопроводам сопровождается потерями её энергии на преодоление сил трения, возникающих при соприкосновении поверхности движущейся жидкости с внутренней поверхностью труб (так называемые линейные потери). Кроме того, дополнительные потери энергии возникают в местах резкого изменения направления (повороты, изгибы) или площади сечения потока жидкости (переходы с одного диаметра труб на другой), при её прохождении через арматуру и измерительные приборы, а также при разделении одного потока на несколько потоков или их объединении в один поток. Средние скорости потока в поперечном сечении трубы связаны с количествами протекающей через это сечение жидкости за единицу времени уравнениями неразрывности потока:
V=fвн wср = 0,785 d²вн wср, (5.2) 
G = fвн wср ρ = 0,785d²внwсрρ, (5.3)
где V – объём, м3/с; G – масса жидкости, протекающей за секунду через сечение трубы площадью в свету fвн, м²; wср - средняя скорость потока, м/с, ρ - плотность жидкости, кг/м3.
Для стационарного течения вязкой жидкости при постоянстве её температуры и скорости в пределах рассматриваемого участка применение закона сохранение энергии к массе потока жидкости приводит к уравнению Бернулли:
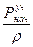 + Z
+ Z 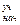 g =
g = 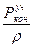 +Z
+Z 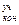 g +
g + 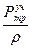 , (5.4)
, (5.4)
или ∆pуч = p 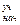 - p
- p 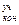 = p
= p 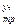 + ρg( Z
+ ρg( Z 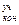 - Z
- Z 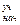 ) , (5.5)
) , (5.5)
где p 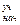 и p
и p 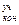 , Па, - давления жидкости в начальном и конечном сечениях труб в пределах участка; ρ, кг/м3 - плотность жидкости; Z
, Па, - давления жидкости в начальном и конечном сечениях труб в пределах участка; ρ, кг/м3 - плотность жидкости; Z 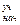
 и Z
и Z 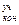 , м, - ординаты, соответствующие центрам начального и конечного сечений трубы относительно произвольной горизонтальной плоскости (геодезические отметки); g, м/с2 - ускорение силы тяжести в гравитационном поле Земли, которое в гидравлических расчетах можно принимать постоянным и равным 9,81 м/с2
, м, - ординаты, соответствующие центрам начального и конечного сечений трубы относительно произвольной горизонтальной плоскости (геодезические отметки); g, м/с2 - ускорение силы тяжести в гравитационном поле Земли, которое в гидравлических расчетах можно принимать постоянным и равным 9,81 м/с2
Величина p 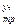 соответствует перепаду давления между начальным и конечным сечениями трубы на участке, вызванному расходом энергии потока жидкости на преодоление сил трения между этим потоком и внутренней поверхностью трубопровода, а также местные потери.
соответствует перепаду давления между начальным и конечным сечениями трубы на участке, вызванному расходом энергии потока жидкости на преодоление сил трения между этим потоком и внутренней поверхностью трубопровода, а также местные потери.
Величина ∆Zуч = Z 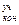 - Z
- Z 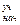 , м, которая может быть либо положительной, либо отрицательной, соответствует разности между геодезическими отметками начального и конечного сечений трубы на участке. Эта величина равна нулю для горизонтально уложенных трубопроводов, а также для любых замкнутых контуров циркуляции жидкости, которые характерны для двухтрубных водяных теплосетей, обычно замыкающихся в источнике теплоснабжения. Поэтому суммарный перепад давлений по всем участкам трубопроводов, образующим такой контур, равен
, м, которая может быть либо положительной, либо отрицательной, соответствует разности между геодезическими отметками начального и конечного сечений трубы на участке. Эта величина равна нулю для горизонтально уложенных трубопроводов, а также для любых замкнутых контуров циркуляции жидкости, которые характерны для двухтрубных водяных теплосетей, обычно замыкающихся в источнике теплоснабжения. Поэтому суммарный перепад давлений по всем участкам трубопроводов, образующим такой контур, равен
∑pуч =∑p 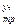 =pс.нач – pс.кон , (5.6)
=pс.нач – pс.кон , (5.6)
В (5.7) pс.нач и pс.кон – значения давления сетевой воды в начальной и конечной точках циркуляционного контура, обычно замыкающегося в источнике теплоснабжения, причем эта разность давлений поддерживается за счет работы циркуляционных сетевых насосов.
В общем случае величина pуч состоит из двух слагаемых, соответствующих линейным и местным потерям, причем линейные потери в пределах участка из труб одного внутреннего диаметра и с одинаковыми на всем протяжении расходами воды пропорциональны длине lуч этого участка. Второе слагаемое ∆pм соответствует местным потерям энергии в пределах участка. Таким образом, имеем
∆pуч = ∆pтрlуч + ∆pм, (5.7)
Здесь ∆pтр, Па/м – удельное падение давления на трение, отнесенное к 1м длины участка.
.
Линейное падение давления. Величина удельного падения давления определяется уравнением д′Арси-Вейсбаха:
∆pтр = λтрρw²ср/2dвн, (5.8)
где λтр - безразмерный коэффициентгидравлическоготрения или гидравлическогосопротивления.
Характеристикой режима течения жидкостей, в частности критерием перехода ламинарного течения в турбулентное, является безразмерный параметр Re (число Рейнольдса). Скорости воды в трубопроводах теплосетей при расчетном режиме обычно находятся в интервале 0,5 – 3,0 м/с. Расчеты показывают, что значения Re, меньшие 2000-2300, соответствующие ламинарному течению, практически не встречаются. При повышении числа Re и переходе ламинарного течения в турбулентное значение коэффициента λтр скачкообразно возрастает с 0,028 – 0,032 до 0,038 – 0,040. При дальнейшем росте числа Re это значение постепенно снижается и при некотором значении Re практически достигает минимального значения. При дальнейшем увеличении числа Re коэффициент гидравлического трения остается постоянным.
Особенностью турбулентного течения в трубах является влияние на значения λтр помимо числа Re шероховатости внутренней поверхности труб, возникающей в основном за счет коррозии этой поверхности. Шероховатую поверхность можно представить состоящей из элементарных выступов высотой k. В качестве первого характеристического параметра шероховатости принимают высоту выступа шероховатости, называемую абсолютной шероховатостью стенки. У большинства работающих стальных трубопроводов она составляет в зависимости от технологии изготовления труб и условий эксплуатации от 0,05 до 2,0 мм. В качестве второго характеристического параметра принимают отношение абсолютной шероховатости к радиусу трубы k/r, называемое относительной шероховатостью. Под эквивалентной относительной шероховатостью реального трубопровода понимается искусственная относительная равномерная шероховатость цилиндрической стенки, коэффициент гидравлического трения которой в области Re › Reпр такой же, как и в данном реальном трубопроводе.
Местное падение давления. Расчет местных потерь энергии при течении воды в различных элементах трубопроводов теплосетей, производится из допущения пропорциональности между этими потерями и кинетической энергией потока жидкости:
∆pм = ξмρw²ср/2, (5.9)
где ξм - безразмерный коэффициент местного сопротивления, зависящий от характера сопротивления. Падение давления в местных сопротивлениях – это падение давления в арматуре (вентилях, задвижках, кранах и т.д.) и других элементах оборудования, не размещенных равномерно по длине трубопровода (коленах, шайбах, переходах и т.п.).
Если представить прямолинейный трубопровод, линейное падение давление на котором равно падению давления в местных сопротивлениях, то длина такого участка трубопровода называется эквивалентной длиной местных сопротивлений. Эти эквивалентные длины lэкв определяются исходя из сопоставления значений ∆pтрlэкв по формуле (5.9) и ∆pм по формуле (5.10). Отсюда
Lэкв = ξмdвн/λтр, (5.10)
Расчеты показывают, что эквивалентная длина местных сопротивлений пропорциональна сумме коэффициентов местных сопротивлений в первой степени и диаметру трубопровода в степени 1,25.
Отношение падения давления в местных сопротивлениях трубопровода к линейному падению в этом трубопроводе представляет собой долю местных потерь. Нетрудно видеть, что доля местных потерь равна отношению эквивалентной длины местных сопротивлений к длине трубопровода.
Сумма падений давления – линейного и в местных сопротивлениях – составляет суммарное падение давления.
Дата добавления: 2019-02-08; просмотров: 1107;











